Hans Walser, [20120505], [20131223a]

Milchkarton und Problem von Deli

1        Fragestellung

Ein quaderfšrmiger Milchkarton habe die Ma§e . Dabei ist a die Breite der Vorderfront, b die Tiefe und c die Hšhe. Die Klebefalze haben die Breite . Am RŸcken ist nur ein einfacher Falz, oben und unten haben wir je einen Doppelfalz.

Wichtig sind die ãFaltnasenÒ in Form eines rechtwinklig gleichschenkligen Dreiecks mit der Hypotenuse b. Es hat vier Faltnasen. Die beiden oberen sind seitlich heruntergeklappt, die beiden unteren auf das Bodenrechteck eingeklappt und daher beim stehenden Milchkarton nicht sichtbar. Die Faltnasen sind doppellagig. Insgesamt benštigen sie eine KartonflŠche von . Wegen dieser Faltnasen muss b im Vergleich mit a und c eher klein gehalten werden. 

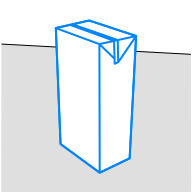
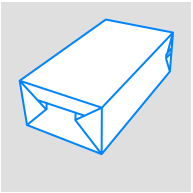
Milchkarton, stehend und liegend

Bei der Abwicklung ergibt sich ein Rechteck (Kartonbedarf) von:

 

 

FŸr das Volumen  haben wir .

Die Aufgabe besteht nun darin, bei gegebenem V und  die Extremstellen der Funktion  zu finden. Die Nebenbedingung ist .

1.1      Erster Rechenweg

Dazu arbeiten wir mit der Hilfsfunktion

 

,

 

in unserem Fall also:

 

 

und suchen Nullstellen des Gradienten von F:

 

 

 

 

 

 

 

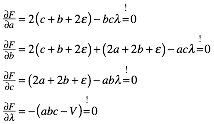
Das ist ein nichtlineares Gleichungssystem mit vier Gleichungen fŸr die Unbekannten a, b, c, .

1.2      Zweiter Rechenweg

Aus  erhalten wir zum Beispiel  und damit:

 

 

Nun suchen wir die Nullstellen des Gradienten von S, also

 

 

 

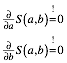
Das ist ein nichtlineares Gleichungssystem mit zwei Gleichungen fŸr die beiden Unbekannten a, b.

2        Beispiel

Wir bearbeiten eine Halbliterpackung fŸr UHT-Milch und rechnen in Dezimetern. Es ist dann . Die Klebefalzbreite ist 8mm, also .

2.1      Minimierung des Kartonbedarfs

Wir arbeiten nach dem ersten Lšsungsweg mit dem Programm

 

DIGITS := 4:

 

V:=0.5:

eps:=0.08:

 

S:=(a,b,c)->(2*a+2*b+eps)*(c+b+2*eps):

Phi:=(a,b,c)->a*b*c-V:

 

F:=(a,b,c, lam)->S(a,b,c)-lam*Phi(a,b,c):

 

glgs:={diff(F(a,b,c,lam), a$1)=0,

       diff(F(a,b,c,lam), b$1)=0,

       diff(F(a,b,c,lam), c$1)=0,

       diff(F(a,b,c,lam), lam$1)=0}:

 

Sol:=solve(glgs, {a,b,c,lam}): print(Sol);

 

und erhalten die folgenden Lšsungen:

 

{[a = - 0.6279 + 0.8293 I, b = - 0.2496 + 0.4358 I,

  c = - 0.3749 + 0.8805 I, lam = - 3.2 - 4.847 I],

 

 [a = - 0.6279 - 0.8293 I, b = - 0.2496 - 0.4358 I,

  c = - 0.3749 - 0.8805 I, lam = - 3.2 + 4.847 I],

 

 [a = 0.4249 + 0.6848 I, b = - 0.4649 - 0.6848 I,

  c = 0.3049 + 0.6848 I, lam = 0],

 

 [a = 0.4249 - 0.6848 I, b = - 0.4649 + 0.6848 I,

  c = 0.3049 - 0.6848 I, lam = 0],

 

 [a = 19.92, b = -0.1591, c = -0.1578, lam = -12.5],

 

 [a = -0.04001, b = -0.04002, c = 312.3, lam = -50.0],

 

 [a = 0.9058, b = 0.4983, c = 1.108, lam = 6.399],

 

 [a = -0.7699, b = 0.7299, c = -0.8899, lam = 0]}

 

Von den acht Lšsungen sind nur vier reell, und nur eine mit positiven reellen Werten, nŠmlich:

 

a = 0.9058, b = 0.4983, c = 1.108, lam = 6.399

 

Der Kartonbedarf ist 5.1007.

2.2      Reale Halbliterpackung

Bei der realen Halbliterpackung messen wir . Der Kartonbedarf dazu ist etwa 5.175.

Wir sehen, dass in der RealitŠt nicht die Minimallšsung gewŠhlt wurde. GegenŸber der Minimallšsung ist die Packung schmaler, dŸnner und deutlich hšher. Der Kartonbedarf ist allerdings nur wenig grš§er.

3        Einfluss der Klebefalzbreite

Um den Einfluss der Breite der Klebefalze zu studieren, vergleichen wir die beiden FŠlle  und .

3.1      V = 1, eps = 0.1

Von den acht Lšsungen sind nur vier reell, und nur eine mit positiven reellen Werten, nŠmlich:

 

a = 1.142, b = 0.6279, c = 1.395, lam = 5.076

 

Der Kartonbedarf ist 8.089.

3.2      V = 1, eps = 0.2

Wir verdoppeln die Breite der Klebefalze und erhalten als reelle positive Lšsung:

 

a = 1.065, b = 0.6237, c = 1.506, lam = 5.386

 

GegenŸber dem obigen Beispiel wird a kleiner, b geringfŸgig kleiner und c grš§er. Der Quader verŠndert also seine Form. Der Kartonbedarf wird etwas grš§er: 8.0996.

4        VernachlŠssigung der Klebefalze

Wir setzen nun . Damit entfernen wir uns von der RealitŠt. Die Resultate sind aber interessant.

4.1      V = 1, eps = 0

Wir erhalten:

 

a = 1.2599, b = 0.62996, c = 1.2599, lam = 4.7622

 

Die Daten kšnnen exakt angegeben werden:

 

 

Wir sehen, dass hier das klassische delische Problem hineinspielt: Die Konstruktion von  ist bei BeschrŠnkung auf die euklidischen Werkzeuge Zirkel und Lineal nicht mšglich.

Der optimale Milchkarton ist ein halber WŸrfel. Der Kartonbedarf ist:

 

 

4.2      V = 0.5, eps = 0

Wir erhalten:

 

a = 1, b = 0.5, c = 1, lam = 6

 

Der optimale Milchkarton ist der halbe EinheitswŸrfel. Der Kartonbedarf ist . An sich hat der halbe EinheitswŸrfel eine OberflŠche von 4. Der Mehrbedarf von 0.5 an Karton ist durch die Faltnasen bedingt.