Hans Walser, [20171028]
Logarithmen und Fibonacci
Anregung: Jo Niemeyer, Berlin
1 Worum geht es?
Da die Fibonacci-Zahlen nŠherungsweise exponentiell wachsen, wachsen die Logarithmen davon nŠherungsweise linear. Es werden numerische und grafische Beispiele dazu gegeben.
2 Der Goldene Logarithmus
Mit 
bezeichnen
wir den Goldenen Schnitt (Walser 2013).
Unter dem
Goldenen Logarithmus verstehen wir den Logarithmus zur Basis 
. Er wird wie folgt berechnet:
(1)
Der natźrliche Logarithmus ln( ) in der Formel (1) kann durch irgend einen anderen Logarithmus ersetzt werden.
3 Die Lucas-Zahlen
Mit den Startwerten 1 und 3 und der źblichen Fibonacci-Rekursion erhalten wir die Luccas-Zahlen:
1, 3, 4, 7, 11, 18, 29, ... (2)
Die Tabelle 1 gibt die Lucas-Zahlen und den Logarithmus zur Goldenen Basis davon.
|
n |
Ln |
|
|
1 |
1 |
0. |
|
2 |
3 |
2.283011831 |
|
3 |
4 |
2.880840183 |
|
4 |
7 |
4.043770434 |
|
5 |
11 |
4.983034810 |
|
6 |
18 |
6.006443753 |
|
7 |
29 |
6.997533430 |
|
8 |
47 |
8.000941383 |
|
9 |
76 |
8.999640321 |
|
10 |
123 |
10.00013738 |
|
11 |
199 |
10.99994754 |
|
12 |
322 |
12.00002005 |
|
13 |
521 |
12.99999236 |
|
14 |
843 |
14.00000294 |
|
15 |
1364 |
14.99999889 |
|
16 |
2207 |
16.00000044 |
|
17 |
3571 |
16.99999985 |
|
18 |
5778 |
18.00000008 |
|
19 |
9349 |
18.99999999 |
|
20 |
15127 |
20.00000003 |
Tab. 1: Lucas-Zahlen und Goldener Logarithmus
Wir sehen, dass sich die Goldenen Logarithmen den natźrlichen Zahlen annŠhern. Hintergrund: Die Lucas-Zahlen kšnnen durch die Formel von Binet generiert werden:
(3)
Der zweite Summand geht gegen null.
Die
Abbildung 1 gibt die ersten zehn Treppenstufen fźr 
.
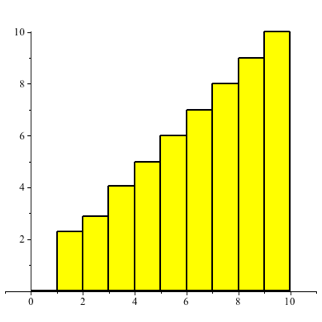
Abb. 1: Treppenstufen
Die Treppe wŠchst zuerst unregelmŠ§ig, und dann immer regelmŠ§iger.
4 Die Fibonacci-Zahlen
Bei den
Fibonacci-Zahlen mźssen wir einen Korrekturterm 
addieren.
|
n |
Fn |
|
|
|
1 |
1 |
0. |
1.672275940 |
|
2 |
1 |
0. |
1.672275940 |
|
3 |
2 |
1.440420092 |
3.112696032 |
|
4 |
3 |
2.283011831 |
3.955287771 |
|
5 |
5 |
3.344551878 |
5.016827818 |
|
6 |
8 |
4.321260276 |
5.993536216 |
|
7 |
13 |
5.330187717 |
7.002463657 |
|
8 |
21 |
6.326782265 |
7.999058205 |
|
9 |
34 |
7.328083693 |
9.000359633 |
|
10 |
55 |
8.327586688 |
9.999862628 |
|
11 |
89 |
9.327776543 |
11.00005248 |
|
12 |
144 |
10.32770403 |
11.99997997 |
|
13 |
233 |
11.32773173 |
13.00000767 |
|
14 |
377 |
12.32772115 |
13.99999709 |
|
15 |
610 |
13.32772519 |
15.00000113 |
|
16 |
987 |
14.32772365 |
15.99999959 |
|
17 |
1597 |
15.32772424 |
17.00000018 |
|
18 |
2584 |
16.32772401 |
17.99999995 |
|
19 |
4181 |
17.32772410 |
19.00000004 |
|
20 |
6765 |
18.32772407 |
20.00000001 |
Tab. 2: Fibonacci-Zahlen
Hintergrund: In der Binet-Formel
(4)
mźssen
wir den Faktor 
austricksen.
Allerdings wźrde die Treppe auch ohne Korrekturterm immer gleichmŠ§iger wachsen. Wir kŠmen aber nicht gegen die natźrlichen Zahlen.
Die
Abbildung 2 gibt die ersten 10 Treppenstufen fźr 
.
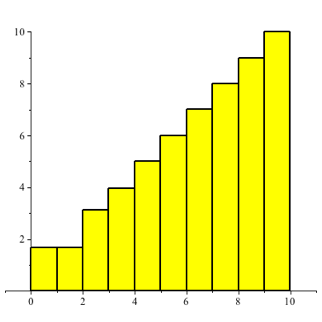
Abb. 2: Treppenstufen
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.