Hans Walser, [20170306]
Lineares bei Pythagoras
Anregung: B. J., B. und E. V., M.
1 Worum geht es?
Die SŠtze im Umfeld des Satzes von Pythagoras sind FlŠchensŠtze. Auch fźr LŠngenberechnungen muss źber den Umweg von FlŠchenberechnungen vorgegangen werden.
Es wird ein Beispiel gezeigt, wo dies nicht der Fall ist.
2 Die Basisfigur
In die kanonische Pythagoras-Figur zeichnen wir die rote Strecke gemŠ§ Abbildung 1. Wie lang ist diese rote Strecke?
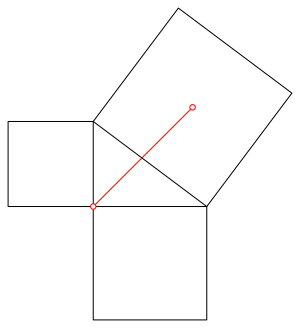
Abb. 1: Wie lang ist die rote Strecke?
3 Bezeichnungen
Wir arbeiten mit den Bezeichnungen der Abbildung 2.
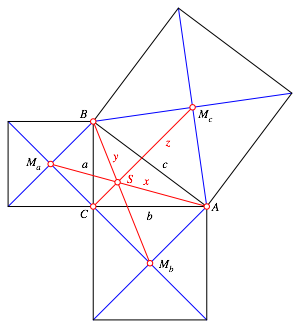
Abb. 2: Bezeichnungen
Gesucht ist die LŠnge der Strecke z.
4 Lšsungswege
Es werden zwei verschiedene Lšsungswege gezeigt.
4.1 Satz des PtolemŠus
Das Viereck AMcBC ist ein Sehnenviereck (Abb. 3). Die vier Punkte liegen auf dem Thaleskreis des Dreieckes ABC.
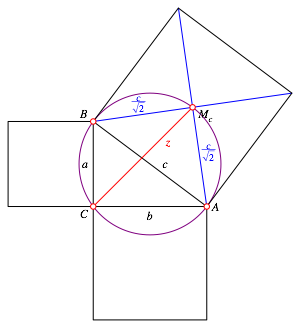
Abb. 3: Sehnenviereck
Nach dem Satz des PtolemŠus gilt daher:
![]() (1)
(1)
Daraus ergibt sich die lineare Beziehung:
![]() (2)
(2)
4.2 Einbetten in Quadrat
Wir betten das Hypotenusenquadrat des rechtwinkligen Dreiecks ABC in ein grš§eres Quadrat ein gemŠ§ Abbildung 4.
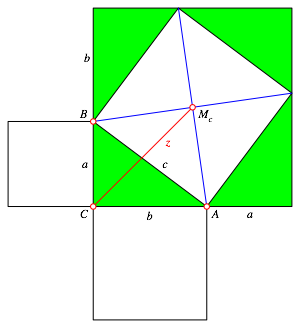
Abb. 4: Einbetten in Quadrat
Dieses grš§ere Quadrat hat die SeitenlŠnge a + b. Die gesuchte LŠnge z ist dessen halbe Diagonale. Damit erhalten wir erneut (2). Zudem zeigt sich, dass die Strecke z die Winkelhalbierende des rechten Winkels des Dreiecks ABC ist.
5 Bemerkungen und ErgŠnzungen
5.1 Gleiche LŠnge
Die Strecke z ist gleich lang wie die Strecke MaMb. Dies ergibt sich unmittelbar aus (2). Die Strecke z ist auch orthogonal zur Strecke MaMb. Dies ergibt sich als Sonderfall des Satzes von van Aubel.
5.2 Quadrat einpassen
Wir kšnnen in die Figur der Abbildung 2 ein weiteres Quadrat einpassen (Abb. 5).
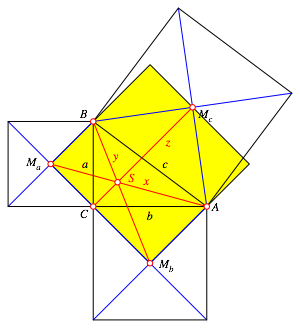
Abb. 5: Quadrat einpassen
5.3 Schnittpunkt
Die drei Strecken x, y, z sind kopunktal, Schnittpunkt S. Dies ist ein Sonderfall eines Satzes von Jacobi (Walser 1991).
Fźr die Strecke CS erhalten wir mit €hnlichkeitsźberlegungen:
![]() (3)
(3)
5.4 FlŠchensatz
Das Dreieck SMaMb ist flŠchenmŠ§ig halb so gro§ wie das rechtwinklige Dreieck ABC (Abb. 6).
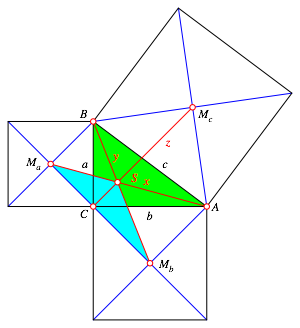
Abb. 6: Halber FlŠcheninhalt
5.5 Die beiden anderen Transversalen
Fźr die Berechnung der LŠngen der Transversalen x und y benštigen wir den Satz des Pythagoras. Das geht also nicht mehr linear.
Literatur
Walser, Hans (1991): Ein Schnittpunktsatz. Praxis der Mathematik (33), 1991, 70-71.