Hans Walser, [20090815a]

Kugelmodelle aus Großkreisen

1 Worum geht es?

Es werden einige Beispiele von Kugelmodellen vorgestellt, welche aus regelmäßig verteilten Großkreisen (Kreisen mit demselben Radius wie die Kugel) bestehen.

Die Großkreise werden aus Plastikband (Verpackungsmaterial), Stahlband (Verpackungsmaterial) oder Peddigband (Bastelmaterial) gebildet. Die Bänder werden gelocht und mit Mustertütenklammern oder Metallschrauben und Muttern verbunden. Die Modelle können im Prinzip wieder auseinander genommen werden.

Verschiedene Modelle eignen sich, um ganze Kugelcluster zu bauen. Dies ist natürlich mit einigem Arbeitsaufwand verbunden.

2 Modell mit drei Großkreisen

Die drei paarweise orthogonalen Großkreise können als Äquator, 0°/180°-Meridian und ±90°-Meridian interpretiert werden.

Es braucht drei Streifen nach folgenden Schema:

Drei Großkreise

Die drei Streifen werden durch je fünf Löcher in vier gleiche Teile geteilt. Die drei Streifen werden zu Großkreisen und einem Kugelmodell zusammengefügt. Für das Gesamtmodell sind sechs Verbindungen nötig.

Es entstehen auf der Kugeloberfläche acht gleichseitige Dreiecke mit je drei rechten Winkeln, also der Winkelsumme 270°. — Die Winkelsumme eines Kugeldreieckes ist nicht konstant, aber immer größer als 180°.

Die Fotos zeigen ein Stahlbandmodell mit Schrauben und ein Plastikbandmodell mit Mustertütenklammern.

Drei Großkreise

Die Kugelmodelle können genau an den Verbindungsstellen der Streifen mit Nachbarkugeln verbunden werden. So entsteht eine raumfüllende Kugelpackung. Sie entspricht der Würfelpackung.

Kugelpackung. Tanz auf der Ecke

3 Modell mit vier Großkreisen

3.1 Basismodell

Es braucht vier Streifen nach folgendem Schema:

Vier Großkreise

Die vier Streifen werden durch je sieben Löcher in sechs gleiche Teile geteilt.

Vier Großkreise

Die vier Großkreise unterteilen die Kugeloberfläche in acht gleichseitige Dreiecke und sechs Quadrate. Wir haben 12 Verbindungen (Schrauben).

Die Großkreise schneiden sich unter Winkeln von . Wir haben also „unschöne“ Winkel. Die Kenntnis dieses Winkels ist aber zur Konstruktion des Modells nicht erforderlich. Der Winkel stellt sich wegen der Eigenstabilität des Modells automatisch ein. — Die Berechnung des Winkels erfordert Formeln aus der sphärischen Trigonometrie.

3.2 Innenleben

Wenn wir an den zwölf Verbindungsstellen Ringschrauben mit dem Ring nach innen anbringen, können wir mit Schnüren vier gleichseitige Dreiecke einziehen, welche sich wechselseitig durchdringen.

Vier Dreiecke im Innern

Es ist auch möglich, einen räumlichen Stern einzuziehen, welcher aus vier ebenen sechsspitzigen Sternen besteht.

Weihnachten kommt bestimmt

3.3 Kugelpackungen

Wir können an den Verbindungsstellen die Kugeln mit Nachbarkugeln zusammenbauen. Dadurch entsteht eine raumfüllende Kugelpackung. Sie entspricht der Packung von Rhombendodekaedern. Es ist die dichteste regelmäßige Kugelpackung. Bereits Johannes Kepler (1571 – 1630) vermutete dies, aber erst 1998 konnte diese Keplersche Vermutung durch Thomas Callister Hales (*1958) mit Computerhilfe bewiesen werden.

Durch geeignete Auswahl erhalten wir verschiedene reguläre und halbreguläre Figuren.

3.3.1 Tetraeder

Wir können vier Kugeln so zusammenfügen, dass ihre Zentren die Ecken eines regulären Tetraeders sind.

Tetraeder

3.3.2 Oktaeder

Aus sechs Kugeln lässt sich ein Oktaeder bauen.

Oktaeder

3.3.3 Würfel

Aus 14 Kugeln gibt es einen Würfel. Acht Kugeln (schwarz) sind die Ecken, sechs Kugeln (grün) die Seitenmitten.

Würfel

3.3.4 Kuboktaeder

Das Bild zeigt 13 Pingpong-Bälle in einer Kugelpackung. Zuinnerst eine blauen Kugel, rundherum 12 weiße Kugeln.

Dreizehn Kugeln

Die zwölf weißen Kugeln sind allerdings nicht so platziert wie die 12 Ecken eines regelmäßigen Ikosaeders. Wir sehen auf der Außenseite sowohl gleichseitige Dreiecke (insgesamt sind es 8) wie auch Quadrate (insgesamt 6). Die Zentren der weißen Kugeln entsprechen den 12 Ecken eines Kuboktaeders.

Wir können nun unser Großkreismodell mit vier Streifen genau mit den Verbindungsstellen der Streifen zu einer solchen Kugelpackung zusammenfügen. Die folgenden beiden Bilder zeigen zwei Mal das gleiche Modell mit 13 Kugeln, das eine Mal so aufgestellt, dass sich in der obersten Etage drei Kugeln befinden, das andere Mal so, dass wir vier Kugeln oben haben.

Drei Kugeln in der obersten Etage

Vier Kugeln in der obersten Etage

3.4 Überlagerung

Das folgende Modell wurde von einem Seminarteilnehmer entdeckt und gebaut.

Kugelmodell

Es besteht aus drei Großkreisen mit Achterteilung und vier Großkreisen mit Sechserteilung und ist eine Überlagerung des Kugelmodells mit drei Großkreisen und des Kugelmodells mit vier Großkreisen.

Drei Großkreise mit Achterteilung, vier Großkreise mit Sechserteilung

Bemerkenswert ist bei diesem Modell folgendes: Während wir bei den Modellen bis jetzt an jeder Verbindungsstelle immer nur eine Verbindung von zwei Großkreisen hatten, haben wir hier zwar auch sechs Verbindungsstellen mit zwei sich orthogonal kreuzenden Großkreisen, aber an den übrigen 12 Verbindungsstellen sind es drei Großkreise. Diese schneiden sich aber nicht regelmäßig, das heißt nicht unter Winkeln von 60°.

4 Modelle mit sechs und zehn Großkreisen

4.1 Modell mit sechs Großkreisen

4.1.1 Basismodell

Es braucht sechs Streifen gemäß Schema:

Sechs Großkreise

Die Streifen werden durch 11 Löcher in zehn Teile unterteilt.

Sechs Großkreise

Die Großkreise unterteilen die Kugeloberfläche in 20 gleichseitige Dreiecke und 12 regelmäßige Fünfecke. Dreiecke und Fünfecke haben dieselbe Seitenlänge. Es sind 30 Verbindungen erforderlich. — Die platonischen Körper lassen grüßen.

Die Großkreise schneiden sich unter Winkeln von . Die Kenntnis dieses Winkels ist aber zur Konstruktion des Modells nicht erforderlich. Die Winkel stellen sich wegen der Eigenstabilität des Modells automatisch ein. — Die Berechnung des Winkels erfordert Formeln der sphärischen Trigonometrie.

4.1.2 Cluster

Es ist nicht möglich, diese Kugeln mit sechs Großkreisen an den Verbindungsstellen so zusammenzufügen, dass eine raumfüllende Kugelpackung entsteht. Hingegen können zwölf solcher Kugeln so zusammengefügt werden, dass deren Zentren die Ecken eines regelmäßigen Ikosaeders bilden.

Ikosaeder

Wir können 20 solcher Kugeln so zusammenfügen, dass deren Zentren die Ecken eines regelmäßigen Dodekaeders bilden.

Dodekaeder

4.1.3 Halbkugel

Bei allen Großkreismodellen können wir einen beliebigen Großkreis als Äquator definieren und dann eine Hemisphäre wegschneiden. Dann bleibt ein Halbkugelmodell übrig.

Halbkugel

Solche Halbkugeln können zur Konstruktion von klassischen Lampenschirmen verwendet werden.

4.1.4 Ein Hybridmodell

Anregung: Matthias Ludwig, Weingarten

Hybridmodell

Das Modell ist kein Großkreismodell, sondern ein Großkreisbogenmodell. Die 30 Großkreisbogen entstehen aus kongruenten Streifen mit vier Löchern. Die beiden äußeren Lochabstände müssen übereinstimmen, der mittlere Lochabstand ist beliebig. Das Modell besteht aus 20 gleichseitigen Dreiecken mit kleiner Seitenlänge und 12 regelmäßigen Fünfecken mit großer Seitenlänge.

Mit denselben Bauteilen kann auch ein Modell gebaut werden, in welchem die Dreiecke die große Seitenlänge haben.

4.2 Zehn Großkreise

4.2.1 Basismodell

Wir brauchen 10 Streifen gemäß Schema:

Zehn Großkreise

Die Streifen werden durch die Löcher in sechs gleiche Teile geteilt.

Zehn Großkreise

Die zehn Großkreise bilden Pentagramme, also Sterne mit 5 Spitzen. Die Verbindungsteile sind an den Sternspitzen.

4.2.2 Lampenschirm

Aus Peddigband und Seidenpapier kann ein Lampenschirm hergestellt werden.

Lampenschirm

Wir sehen an den Verbindungsstellen noch die Löcher an den Sternspitzen, in denen während der Trocknung des Leims die Fixierschrauben staken.

4.3 Kombination

Das Modell aus 6 Großkreisen mit Zehnerteilung und das Modell aus 10 Großkreisen mit Sechserteilung benötigen nicht nur gleich viele (nämlich 30) Verbindungsteile, sondern diese Verbindungsstellen sind für beide Modelle an denselben Punkten der Kugeloberfläche. Wir können daher die beiden Modelle überlagern.

Überlagerung

Wir haben dann 12 Fünfecke mit Diagonalen sowie 20 Dreiecke.

Die Diagonalen und die Seitenlängen der Fünfecke stehen in diesem Modell in einem rationalen Verhältnis , während in einem ebenen Fünfeck die Diagonalen zu den Seitenlängen im Verhältnis des goldenen Schnittes stehen, also . Dieses Verhältnis ist irrational (vgl. [Walser 2009], S. 37f).

5 Modelle aus Großkreisbogen

Bis jetzt bestanden unsere Großkreismodelle aus vollständigen Großkreisen. In den folgenden Kugelmodellen haben wir es jedoch nur noch mit Großkreisbogen zu tun.

5.1 Kugelmodelle der platonischen Körper

Wir denken uns jeden platonischen Körper vom Mittelpunkt aus zentral auf seine Umkugel projiziert. Die Kanten der platonischen Körper werden dann zu Großkreisbogen.

5.1.1 Tetraeder

5.1.1.1 Basismodell

Großkreisbogenmodell des Tetraeders

Das Modell besteht aus sechs Großkreisbogen, weil das Tetraeder sechs Kanten aufweist. Das Modell hat (im Unterschied zu Modellen mit durchgehenden Großkreisen) bei „lockeren Schrauben“ keine Eigenstabilität. Es müssen Schrauben (am besten mit Unterlegscheiben) verwendet und fest angezogen werden.

5.1.1.2 Ergänzen der Großkreisbogen. Symmetriegruppe

Natürlich können wir die sechs Großkreisbogen zu vollständigen Großkreisen ergänzen und erhalten dann ein Modell mit sechs durchgehenden Großkreisen.

Sechs Großkreise

Dieses Modell aus sechs Großkreisen unterscheidet sich wesentlich vom regelmäßigen Modell aus sechs Großkreisen mit Zehnerteilung, das wir schon angetroffen hatten.

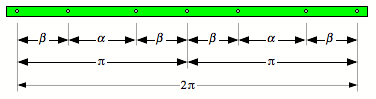
Es sind insgesamt 14 Verbindungen vorhanden. Bei 6 Verbindungen kreuzen sich je zwei Großkreise orthogonal, bei den restlichen 8 Verbindungen haben wir drei Großkreise, die sich gleichmäßig unter Winkeln von 60° schneiden. Die Winkel sind also „schön“. Hingegen ist die Unterteilung der für die Großkreise erforderlichen Streifen nicht mehr regelmäßig. Die Vermaßung im folgenden Schema ist auf der Einheitskugel bezogen, der Umfang eines Großkreises also .

Sechs Streifen

Die Berechnung erfordert sphärische Trigonometrie.

Die Großkreise unterteilen die Kugeloberfläche in 24 kongruente Dreiecke. Diese sind rechtwinklig gleichschenklig. Wenn wir ein Dreieck als Ausgangsdreieck auswählen, gibt es also 24 Abbildungen (die identische Abbildung mit eingerechnet) auf ein weiteres Dreieck der Kugel. Es gibt daher 24 Abbildungen, welche das Kugelmodell auf sich abbilden. Die Symmetriegruppe dieses Kugelmodells enthält also 24 Abbildungen. Wenn wir das ursprüngliche Tetraeder dazudenken, sehen wir, dass dies auch die Symmetriegruppe des Tetraeders ist.

Wir haben somit eine einfache Visualisierung dieser Symmetriegruppe.

5.1.2 Würfel

5.1.2.1 Basis

Großkreisbogenmodell des Würfels

Wir brauchen zwölf Großkreisbogen.

5.1.2.2 Kugelpackung

Mit dem Großkreisbogenmodell des Würfels kann eine raumfüllende Kugelpackung konstruiert werden. Dabei können die Streifen „durchgezogen“ werden, gehen dabei aber auf die anschließende Kugel über.

Kugelpackung

5.1.3 Oktaeder

Das Oktaeder ist eine Ausnahme, indem die Großkreisbogen sich zu durchgehenden Großkreisen ergänzen. Wir erhalten das Modell mit den drei Großkreisen.

5.1.4 Ikosaeder und Dodekaeder

5.1.4.1 Basismodell

Großkreisbogenmodell des Ikosaeders

Wir benötigen 30 Großkreisbogen. Je zwei gegenüberliegende Großkreisbogen gehören zum selben Großkreis.

Analog kann mit 30 Großkreisbogen ein Kugelmodell des Dodekaeders gebaut werden.

5.1.4.2 Ergänzungsbogenmodell

Wir haben vorangehenden gesehen, dass je zwei gegenüberliegende Großkreisbogen zum selben Großkreis gehören. Somit hat es auf diesem Großkreis auch zwei gegenüberliegende Ergänzungsbogen. Wir können auch mit diesen Ergänzungsbogen ein Kugelmodell bauen.

Ergänzungsbogenmodell

Außer den Endverbindungen haben wir zusätzlich Binnenverbindungen. Die drei Abschnitte auf dem Ergänzungsbogen sind aber nicht gleichmäßig. Der grün eingefärbte Teil der Maßskizze entspricht einem einzelnen Bauteil. Die Maßangaben sind auf die Einheitskugel bezogen, auf der ein Großkreis die Länge hat. Für die Berechnung der Unterteilung benötigen wir den goldenen Schnitt (vgl. [Walser 2009]):

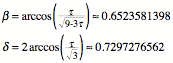
30 Großkreisbogen

Der Ergänzungsbogen und seine Vermaßung ist Teil des Symmetriegruppenmodells von Idosaeder und Dodekaeder (Abschnitt 6.3).

Lampenschirm auf der Basis des Ergänzungsbogenmodells

6 Symmetriegruppen der platonischen Körper

Wir schneiden die Umkugel eines platonischen Körpers mit sämtlichen Symmetrieebenen dieses Körpers. Dadurch erhalten wir Großkreise für ein Großkreismodell.

6.1 Tetraeder

Das zur Symmetriegruppe gehörende Großkreismodell wurde oben schon besprochen.

6.2 Würfel und Oktaeder

Würfel und Oktaeder haben dieselbe Symmetriegruppe. Sie haben neun Symmetrieebenen. Das Symmetriegruppenmodell besteht entsprechend aus neun Großkreisen.

Symmetriegruppe von Würfel und Oktaeder

Es gibt insgesamt 26 Schnittpunkte. Bei 12 Schnittpunkten schneiden sich zwei Großkreise orthogonal, bei 8 weiteren Schnittpunkten schneiden sich drei Großkreise unter Winkeln von 60° und bei den restlichen 6 Schnittpunkten scheiden sich vier Großkreise unter 45°. Wir haben also „schöne“ Schnittwinkel. Wenn wir wie auf der Foto bei den Schnittpunkten von drei Großkreisen auf eine Verbindung verzichten (es hält auch ohne diese), haben wir auch eine schöne Teilung: Drei Streifen (im Bild schwarz) haben eine Achterteilung, die restlichen sechs (im Bild grün) eine Viererteilung. Falls doch eine Verbindung an den Schnittpunkten mit drei Großkreisen gewünscht ist, müssen die sechs Streifen mit der Viererteilung zusätzlich so gelocht werden wie beim Symmetriegruppenmodell des Tetraeders.

Die neun Großkreise unseres Modells unterteilen die Kugeloberfläche in 48 kongruente rechtwinklige Dreiecke. Die Symmetriegruppe von Würfel und Oktaeder besteht aus 48 Elementen.

6.3 Ikosaeder und Dodekaeder

Ikosaeder und Dodekaeder haben dieselbe Symmetriegruppe. Sie haben 15 Symmetrieebenen. Das zugehörige Großkreismodell besteht aus 15 Großkreisen.

Symmetriegruppe von Ikosaeder und Dodekaeder

Wir haben 62 Schnittpunkte. Bei 30 Schnittpunkten schneiden sich zwei Großkreise orthogonal, bei 20 Schnittpunkten haben wir drei Großkreise unter Winkeln von 60° und bei 12 Schnittpunkten fünf Großkreise unter Winkeln von 36°. Wir kommen mit einem einzigen Streifentyp aus, der allerdings unregelmäßig geteilt ist. Für die Berechnung der Teilung benötigen wir den goldenen Schnitt:

Damit erhalten wir für die Streifenteilung, bezogen auf die Einheitskugel:

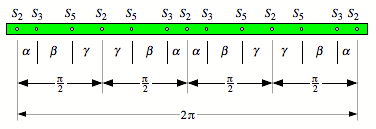
15 Streifen

Beim Modell auf der Foto fehlen die Verbindungen bei den Punkten , also den Schnittpunkten von drei Großkreisen.

Die 15 Großkreise unseres Modells unterteilen die Kugeloberfläche in 120 kongruente rechtwinklige Dreiecke. Die Symmetriegruppe von Ikosaeder und Dodekaeder besteht somit aus 120 Elementen.

6.4 Überlagerungen

Sämtliche von uns besprochenen Großkreis- und Großkreisbogenmodelle passen zu einer der drei Symmetriegruppen der platonischen Körper. Sie können daher mit denselben Verbindungen auf eine der drei Symmetriegruppenkugeln überlagert werden.

Eine Ausnahme bilden die Hybridmodelle, welche nicht die volle Symmetriegruppe der zugehörigen platonischen Körper haben, sondern lediglich die Drehgruppe. Die Hybridmodelle lassen keine Ebenenspiegelungen zu.

7 Gelenkgeometrie

7.1 Würfel und Oktaeder

Wenn wir beim Modell mit vier Großkreisen in regelmäßiger Sechserteilung in der Mitte der Großkreisbogen gelenkig unterteilen und auch die Verbindungen gelenkig gestalten, erhalten wir ein sphärisches Gelenkmodell mit 12 Scheren.

12 Scheren

Wir können nun die Scheren simultan so schließen, dass die Endpunkte der Scheren, also die gelenkigen Verbindungen mit den Nachbarscheren, gegen die Zentren der Dreieck auf der Kugel wandern. Dann erhalten wir ein Großkreisbogenmodell des Würfels.

Wir können die Scheren aber auch so schließen, dass die Endpunkte gegen die Mitten der Quadrate wandern. Dann erhalten wir ein Großkreisbogenmodell des Oktaeders.

Geschlossene Scheren. Würfel oder Oktaeder

In der Tatsache, dass wir mit demselben Modell sowohl Würfel wie auch Oktaeder erreichen können, zeigt sich die so genannte Dualität dieser beiden Körper.

7.2 Tetraeder

Aus dem Modell mit den drei Großkreisen in Viererteilung können wir ein Modell mit sechs Scheren bauen.

Sechs Scheren — Tetraeder

Hier haben wir auf beiden Seiten der Scheren Dreiecke. Wenn wir die Scheren schließen, erhalten wir so oder so ein Großkreisbogenmodell des Tetraeders. Das Tetraeder ist selbstdual.

7.3 Ikosaeder und Dodekaeder

Aus dem Modell mit sechs Großkreisen in Zehnerteilung erhalten wir entsprechend ein Modell mit 30 Scheren. Dieses führt einerseits zum Ikosaeder und andererseits zum dazu dualen Dodekaeder.

8 Die Standardkugel

Wir bauen ein Modell mit Meridianen und Breitenkreisen. Dieses Modell ist natürlich kein reines Großkreismodell, da die Breitkreise mit Ausnahme des Äquators Kleinkreise sind.

Meridiane und Breitenkreise

Das Modell hat eine 30°-Rasterung. Wir haben also sechs Doppelmeridiane sowie den Äquator mit je einer regelmäßigen Zwölferteilung. Spannend wird es bei den Breitenkreisen. Diese müssen wir zusammenstückeln (und erhalten auch so nur eine Approximation der Breitenkreise). Die Breitenkreise sind eben auch seitwärts gekrümmt (so genannte geodätische Krümmung). Der Radius der Breitenkreise reduziert sich gegenüber dem Äquatorradius mit dem Kosinus der geographischen Breite. Der obere Breitenkreis mit der geographischen Breite 60° ist wegen genau halb so lang wie der Äquator. Wir müssen also den Teilungsabstand des Äquators halbieren und zwölf (plus zwölf für die Südseite) Teilstücke mit dem halben Teilungsabstand zwischen den Löchern machen. Für den Breitenkreis zur geographischen Breite 30° haben wir den Reduktionsfaktor .

Die Seitenkrümmung der Breitenkreise sehen wir deutlich, wenn wir vom Polarstern aus auf den Nordpol gucken.

Blick auf den Nordpol

9 Tipps

9.1 Didaktisches

Für Unterricht, Seminarien und Fortbildungskurse eignen sich am besten Modelle aus Plastikband mit Mustertütenklammern. Die Modelle sind etwas elastisch, aber erstaunlich stabil und sehr leicht. Ballspiel ist durch aus möglich.

9.2 Technisches

9.2.1 Material

Breite der Bänder 10mm – 15mm.

9.2.1.1 Plastikband

Für die Löcher ist eine Lederlochzange im Prinzip möglich, aber bei Großauflagen nicht zu empfehlen. Besser eine Bohrmaschine mit 3.5mm-Bohrer. Plastikband hat eine Tendenz, beim Lochen der äußersten Löcher einzureißen. Daher einigen Abstand lassen und nach dem Lochen die vorstehenden Enden verkürzen. Verbindungen bevorzugt mit Mustertütenklammern, bei Großkreisbogenmodellen unter Umständen Verbindungen mit festgezogenen M3-Schrauben und Unterlegscheiben.

9.2.1.2 Peddigband

Peddigband ist recht weich und kann mit einer Lederlochzange gelocht werden. Geeignet für Lampenschirme, da Seidenpapier angeklebt werden kann. Verbindungen mit Weißleim, zum Fixieren Schrauben mit beidseitigen Unterlegscheiben verwenden, die nach dem Trockenen des Leims entfernt werden. Es bleibt dann nur noch das Bohrloch übrig, das dem Design zugerechnet werden kann.

Bei einem Lampenschirm wird dann zunächst eine Kartonschablone für jedes Teilstück auf der Kugeloberfläche geschnitten, die Seitenpapierteile entsprechend zugeschnitten und dann von innen mit Weißleim an das Peddigband geklebt. — Bei einer Lampe muss oben und unten ein Flächenstück zur Luftzirkulation offen gelassen werden, um Hitzestau zu vermeiden.

9.2.1.3 Stahlband

Stahlband ist schwer und braucht HSS-Bohrer. Verbindung mit M3-Schrauben und Muttern. Geeignet für Modelle mit großem Durchmesser und Demo-Modelle.

9.2.1.4 Bänder aus Papier

Wir können auch durch mehrfaches Falten eines Papierblattes zu einem Streifen kommen. Lochen mit der Lederlochzange, Verbinden mit Mustertütenklammern.

Streifen aus Papier

9.2.2 Arbeitsvorgehen

9.2.2.1 Bohren

Für größere Auflagen ist es hilfreich, zuerst eine Bohrlehre (Schablone) aus Metall oder Hartholz mit den nötigen Lochabständen herzustellen. Dann können mehrere Rohstreifen mit Schraubzwingen darunter geklemmt und in einem Durchgang simultan gelocht werden. Bei Plastikstreifen kann es bei hohen Drehzahlen der Bohrmaschine infolge der Hitzeentwicklung zu Verschweißungen der Streifen an den Bohrlöchern kommen. Diese können mit einem scharfen Messer getrennt werden.

9.2.2.2 Flechten

Bei Modellen mit Verbindungsstellen von ausschließlich zwei Großkreisen kann beim Zusammenbau für die Streifen eine Flechttopologie verwendet werden, indem ein Streifen abwechslungsweise oberhalb und unterhalb des kreuzenden Streifens verläuft. Aus ästhetischen Gründen ist es sinnvoll, die beiden sich überlappenden Enden eines Streifens — also das sich Schließen des Großkreises — unterhalb des kreuzenden Streifens zu arrangieren.

Literatur

[Walser 2009] Walser, Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1.