Hans Walser, [20170526]

Kreispackungen

Anregung: Heinz Klaus Strick, Leverkusen. Siehe auch (Strick 2017, S. 269f).

1 Ausgangslage

Wir arbeiten mit zwei Kreisscharen (Abb. 1).

Abb. 1: Zwei Kreisscharen

Die Mittelpunkte der roten Schar bilden einen Quadratraster, die Mittelpunkte der grünen Schar den dualen Quadratraster. Die roten und grünen Kreise berühren einander. Wir haben einen freien Parameter, das Verhältnis der beiden Radien.

Gesucht sind nun weitere Kreise mit dem Mittelpunkt im Zentrum eines roten Kreises, welche eine nicht triviale Auswahl von roten und/oder grünen Kreisen berühren.

Im Folgenden einige eher zufällig gefundene Beispiele. Beweise durch nachrechnen. Für die rechnerischen Nachweise habe ich die Maschenweite der Quadratraster auf 2 gesetzt. Die beiden Radien ergänzen sich dann auf .

Die Studie ist letztlich nur eine Fleißarbeit.

2 Beispiele zu gegebenem Radienverhältnis

In den folgenden Beispielen ist das Radienverhältnis vorgegeben.

2.1 Radienverhältni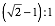s

In diesem Fall berühren sich die grünen Kreise untereinander (Abb. 2). Der rote Radius ist , der grüne Radius 1.

Abb. 2: Grüne Kreise berühren sich

2.1.1 Minimalbeispiel

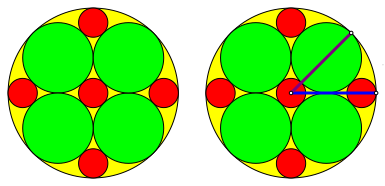
Abb. 3: Minimalbeispiel. Beweisfigur

Wir haben zu zeigen, dass der blaue Radius gleich dem lila Radius ist. Es ist:

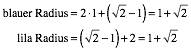(1)

2.1.2 Beispiel

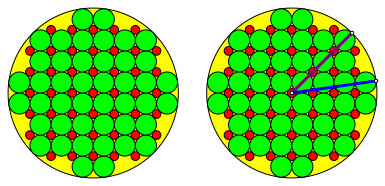
Abb. 4: Beispiel

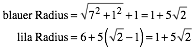(2)

2.1.3 Beispiel

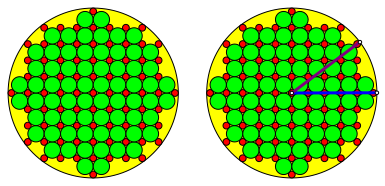
Abb. 5: Beispiel

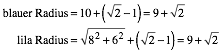(3)

Gibt es weitere Beispiele?

2.1.4 Falsches Beispiel

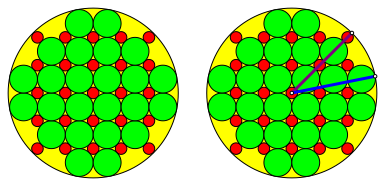
Abb. 6: Falsches Beispiel

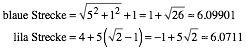(4)

2.2 Radienverhältni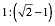s

In diesem Fall berühren sich die roten Kreise untereinander. Der rote Radius ist 1, der grüne Radius .

2.2.1 Beispiel

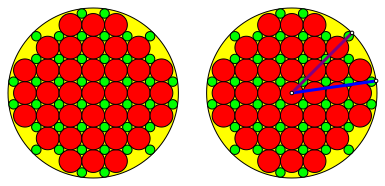
Abb. 7: Beispiel

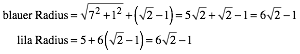(5)

2.2.2 Falsches Beispiel

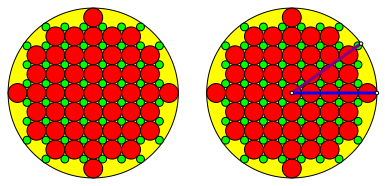
Abb. 8: Falsches Beispiel

(6)

2.3 Gleiche Radien

Beide Radien sind .

2.3.1 Beispiel

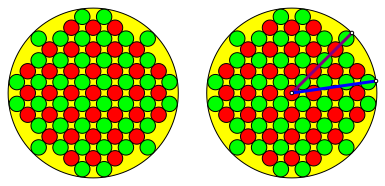
Abb. 9: Beispiel

(7)

2.3.2 Beispiel

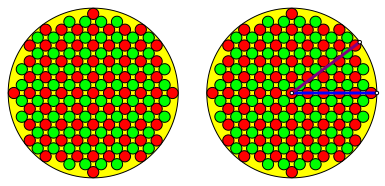
Abb. 10: Beispiel

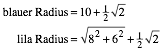(8)

2.4 Radienverhältnis im Goldenen Schnitt

Die Radien sind im Verhältnis . Über den Goldenen Schnitt siehe (Walser 2013).

Der rote Radius ist , der grüne Radius ist .

2.4.1 Beispiel

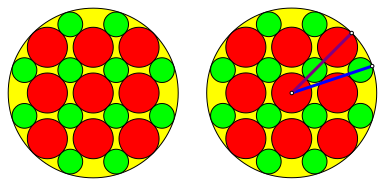
Abb. 11: Radien im Goldenen Schnitt

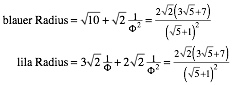(9)

Für die Umformungen wurde CAS (Maple) verwendet. Vergleiche auch [1].

2.4.2 Beispiel

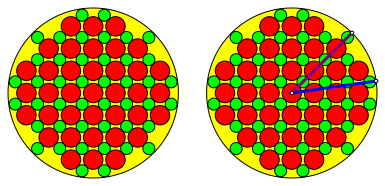
Abb. 12: Radien im Goldenen Schnitt

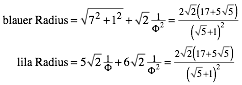(10)

Für die Umformungen wurde CAS (Maple) verwendet.

2.4.3 Gemischtes Beispiel

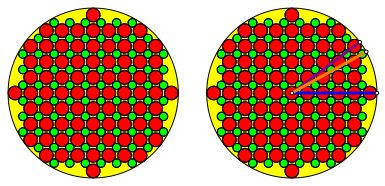
Abb. 13: Gemisches Beispiel

Zunächst ist:

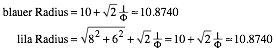(11)

Hingegen ist:

(12)

Die kleinen grünen Kreise berühren den Rand des gelben Kreises nicht.

2.4.4 Falsches Beispiel

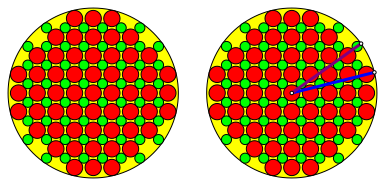
Abb. 14: Falsches Beispiel

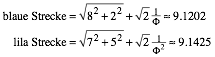(13)

2.5 Radienverhältnis im Goldenen Schnitt

Die Radien sind im Verhältnis . Nun sind die grünen Kreise die dicken.

Der rote Radius ist , der grüne Radius .

2.5.1 Beispiel

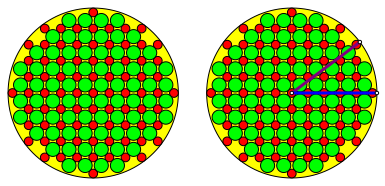
Abb. 15: Beispiel

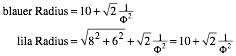(14)

Eigentlich sind Beispiele wie dieses als trivial einzustufen, das sie auf einem pythagoreischen Dreieck beruhen.

3 Radienverhältnis gesucht

Wir gehen von einer stimmigen Figur aus und suchen das passende Radienverhältnis.

3.1 Beispiel

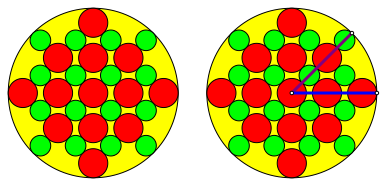
Abb. 16: Beispiel

Wir erhalten für die Radien r_rot und r_grün die Bedingung:

(15)

Der blaue und der lila Radius müssen gleich sein. Zudem ergänzen sich der rote und der grüne Radius auf . Somit erhalten wir das Gleichungssystem:

(16)

Das Gleichungssystem (16) hat die Lösung:

(17)

Das Radienverhältnis ist somit:

(18)

Das ist das Seitenverhältnis im DIN-Format.

3.2 Beispiel

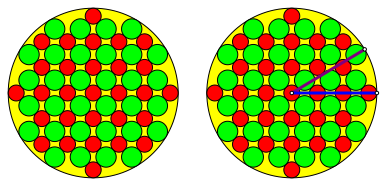
Abb. 17: Beispiel

Wir erhalten die Bedingung:

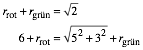(19)

Dazu die Lösungen:

(20)

Das ist nicht mehr so schön.

Literatur

Strick, Heinz Klaus (2017): Mathematik ist schön. Anregungen zum Anschauen und Erforschen für Menschen zwischen 9 und 99 Jahren. Berlin: Springer. ISBN 978-3-662-53729-9.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Websites

[1] Hans Walser: Kreise im Goldenen Schnitt (abgerufen 26. 05. 2017):

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreise_im_GS/Kreise_im_GS.htm