Hans Walser, [20210605]
Hyperboloid-Stern
1 Worum geht es?
Mit drei Rotationshyperboloiden bauen wir einen dem Kepler-Stern (stella octangula) verwandten Stern.
2 Rotationshyperboloid
Unser Rotationshyperboloid (Abb. 1) hat eine gleichseitige Hyperbel als Profilkurve und die z-Achse als Rotationsachse.

Abb. 1: Rotationshyperboloid
Das Rotationshyperboloid enthlt zwei Geradenscharen (Abb. 2). Es ist eine Regelflche. Die Geraden haben gegenber der Rotationsachse einen Winkel von 45¡.
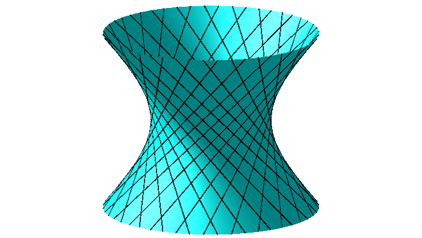
Abb. 2: Geradenscharen
3 Hyperboloide mit orthogonalen Achsen
Wir arbeiten nun weiter mit drei Hyperboloiden, welche paarweise orthogonale Achsen haben (Abb.3).

Abb. 3: Orthogonale Achsen
In der Abbildung 4 sind alle drei Hyperboloide mit gemeinsamem Zentrum gezeichnet.

Abb. 4: Gemeinsames Zentrum
4 Schnittfigur
Wir bilden nun den Durchschnitt aller drei Hyperboloide (Abb. 5). Es entsteht ein Stern.
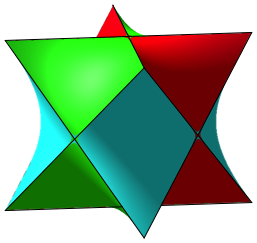
Abb. 5: Hyperboloid-Stern
Die Seitenflchen knnen als hyperbolische Rhomben bezeichnet werden. Es sind zwlf Stck. Wir haben also ein hyperbolisches Rhombendodekaeder.
In der Abbildung 6 sind zustzlich die Geradenscharen eingezeichnet.
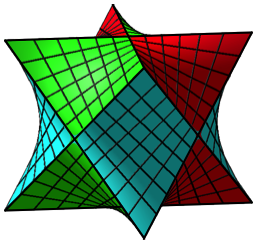
Abb. 6: Geradenscharen
5 Vergleich mit Kepler-Stern
Wir sehen die Analogie zum Kepler-Stern (Abb. 7). Statt zwei gleichseitigen Dreiecken (zum Beispiel die hellblauen Dreiecke mit gemeinsamer Kante) haben wir einen hyperbolischen Rhombus.

Abb. 7: Vergleich mit Kepler-Stern
Beide Figuren passen in einen Wrfel (Abb. 8). Der Kepler-Stern liegt im Hyperboloid-Stern.
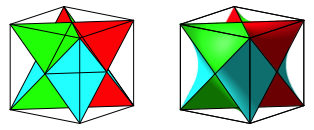
Abb. 8: Im Wrfel
6 Volumen
Das Volumen des Kepler-Sterns ist die Hlfte des Wrfelvolumens.
Fr die Volumenberechnung des Hyperboloid-Sterns verwenden wir ein Koordinatensystem (Abb. 9a) mit dem Ursprung in der Wrfelmitte. Die Einheitspunkte sind die Schnittpunkte der Seitenflchendiagonalen. Der Wrfel hat also die Kantenlnge a = 2 und damit das Volumen 8.
Entsprechend hat der Kepler-Stern das Volumen 4.
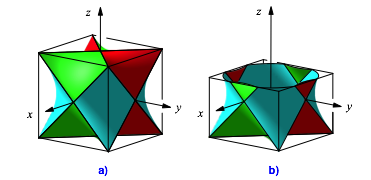
Abb. 9: Koordinatensystem. Horizontaler Schnitt
Nun schneiden wir den Hyperboloid-Stern horizontal auf der Hhe h (Abb. 9b fr die Hhe h = 0.4).
Die Abbildung 10a zeigt die Niveaulinie fr diese Hhe h = 0.4. Beim hellblauen Hyperboloid mit der z-Achse als Drehachse liegen die Niveaulinien auf Kreisen. Da die Seitenflchendiagonalen des Quadrates einen Neigungswinkel 45¡ haben, knnen wir die Hhe h direkt ablesen (Abb. 10b) und damit den Kreisradius bestimmen.
Bei den beiden anderen Hyperboloiden liegen die Niveaulinien auf gleichseitigen Hyperbeln.
Zustzlich sind auch die Niveaulinien des innenliegenden Kepler-Sterns eingezeichnet.
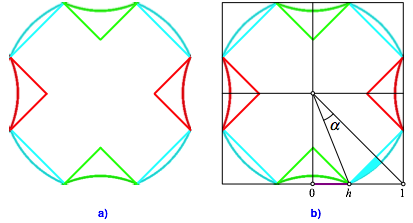
Abb. 10: Niveaulinie
Das Volumen des Hyperboloid-Sterns berechnen wir nun wie folgt. Wir gehen aus vom Volumen des Kepler-Sterns und berechnen unter jedem hyperbolischen Rhombus das Differenzvolumen zum Keplerstern. Dazu mssen wir beispielsweise das in der Abbildung 10b hellblau eingezeichnete halbe Kreissegment fr h von 0 bis 1 aufintegrieren. Dies liefert einen Viertel des Differenzvolumens unter diesem hellblauen hyperbolischen Rhombus.
Im Formeln:
Der Radius r des hellblauen Niveaukreises ist:
![]() (1)
(1)
Weiter ist:
![]() (2)
(2)
Fr den Flcheninhalt A des halben Kreissegmentes ergibt sich:
![]() (3)
(3)
Also wegen (1) und (2):
![]() (4)
(4)
Das gesamte Differenzvolumen VDifferenz ist nun:
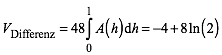 (5)
(5)
Der Autor gesteht, dass er das Integral (5) mit CAS ermittelt hat.
Wegen dem Volumen 4 des Kepler-Sterns erhalten wir schlie§lich fr das Volumen V des Hyperboloid-Sternes:
![]() (6)
(6)
Fr einen dem Einheitswrfel einbeschriebenen Hyperboloid-Stern ergibt sich entsprechend das Volumen ln(2), und fr einen dem Wrfel mit der Kantenlnge a einbeschriebenen Hyprboloid-Stern erhalten wir:
![]() (7)
(7)
Websites
Hans
Walser: Kepler-Stern-Abwicklung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kepler-Stern-Abwicklung/Kepler-Stern-Abwicklung.htm
Hans Walser: Paraboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/P/Paraboloid-Stern/Paraboloid-Stern.htm
Hans Walser: Pyramidoid
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidoid/Pyramidoid.htm
Hans Walser: Sphroid
http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaeroid/Sphaeroid.htm
Hans Walser: Paraboloid-Stern