1 Segner an Euler

Am 29. Januar 1763 schrieb Segner in einem Brief an Euler:

„... das schœne Problem, welches Er Wohlgb. mir mitzutheilen die Geneigt[heit] haben ist einige Probe davon. Ich will bey Gelegenheit die Auflœsung versuchen; aber ich muss Zeit haben; denn es war mir so gar neu, daß bey einem Dreyecke die intersectio trium perpendiculorum ein eintziges Punct sey. Als ich diesem nachdachte, fand ich zugleich, daß die geraden Linien, welche von diesem Punct an die Ecken des Dreyecks gezogen werden kœnnen, sich wie die Cosinus dieser Ecken oder Winckel verhalten. Er Wohlgb. haben dieses ohnfehlbar auch bemercket.“

2 Interpretation

In einem Dreieck mit Höhenschnittpunkt H seien die Höhenabschnitte (Fig. 1).

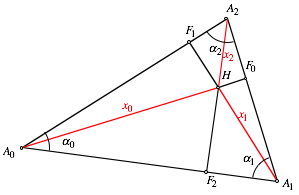
Fig. 1: Höhenabschnitte

Mit den Dreieckswinkeln gilt die Behauptung:

3 Beweis

Das Viereck hat bei und je einen rechten Winkel und bei den Winkel . Daher hat es bei H den Winkel . Als Scheitelwinkel ist dann auch .

Wir spiegeln nun den Höhenschnittpunkt H an der Seite (Fig. 2), der Bildpunkt sei . Bei haben wir ebenfalls den Winkel .

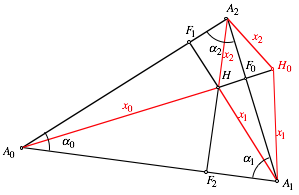
Fig. 2: Spiegeln des Höhenschnittpunktes

Das Viereck ist daher ein Sehnenviereck. Sein Umkreis ist aber der Umkreis u des Dreieckes (Fig. 3).

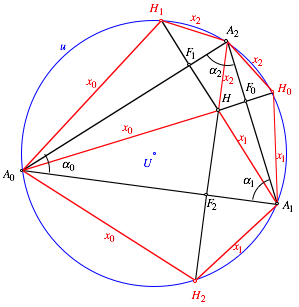
Fig. 3: Spiegelpunkte auf dem Umkreis

Wenn wir H an den beiden anderen Dreiecksseiten spiegeln, erhalten wir entsprechend die Punkte und , welche ebenfalls auf dem Umkreis u des Dreieckes liegen .

Das Sehnensechseck hat folgende Eigenschaften: Die mit der Ecke inzidenten Seiten messen . An der Ecke misst der Innenwinkel .

Wir teilen nun das Sechseck vom Umkreismittelpunkt U aus mit Radien in sechs gleichschenklige Dreiecke auf (Fig. 4).

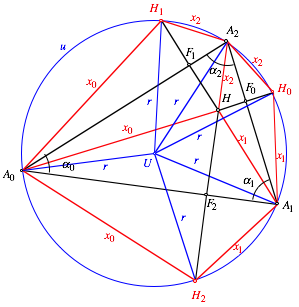
Fig. 4: Aufteilung in gleichschenklige Dreiecke

Dann sind zum Beispiel die beiden Dreiecke und kongruent. Sie haben die Schenkellänge r des Umkreisradius, die Basislänge und die Basiswinkel . Daher ist . Analog folgt für .

Somit haben wir

also die Behauptung von Segner.

Auffallend ist die formale Ähnlichkeit zum Sinussatz.