Hans Walser, [20190709]
FrŽgier
1 Worum geht es?
Zusammenhang zwischen dem FrŽgier-Kegelschnitt und der Evolute.
Zusammenstellung von Resultaten.
Formeln im Anhang.
2 Der Satz von FrŽgier
Der Satz von M. FrŽgier (1815) besagt folgendes:
Werden einem Kegelschnitt c rechtwinklige Dreiecke einbeschrieben derart dass sie eine gemeinsame Rechtwinkelecke C haben, so gehen deren Hypotenusen durch einen gemeinsamen Punkt F.
Den Punkt F nennen wir FrŽgier-Punkt zu C bezźglich c.
Die Abbildung 1 illustriert den Sachverhalt fźr eine Ellipse.
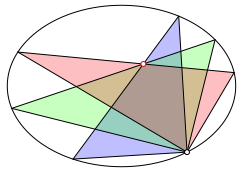
Abb. 1: Satz von FrŽgier
Im Sonderfall eines Kreises ist der FrŽgier-Punkt dessen Zentrum.
3 FrŽgier-Kegelschnitte
Die Menge der FrŽgier-Punkte zu sŠmtlichen Punkten eines Kegelschnittes bildet wieder einen Kegelschnitt. Wir bezeichnen ihn als FrŽgier-Kegelschnitt. Im Falle einer Parabel ist die FrŽgier-Parabel eine kongruente, aber verschobene Parabel. Im Falle einer Ellipse oder Hyperbel ist der FrŽgier-Kegelschnitt eine dazu zentrisch Šhnliche Ellipse beziehungsweise Hyperbel.
In den folgenden Beispielen ist der gegebene Kegelschnitt schwarz gezeichnet, der zugehšrige FrŽgier-Kegelschnitt rot.
ZusŠtzlich ist die Evolute des gegebenen Kegelschnittes in blau eingezeichnet.
Der FrŽgier-Kegelschnitt und die Evolute berźhren sich. Die Berźhrungstangenten (grźn) sind orthogonal.
3.1 Parabel
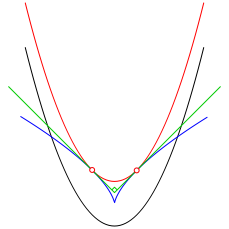
Abb. 2: Parabel
3.2 Ellipse
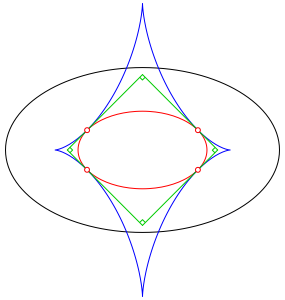
Abb. 3: Ellipse
3.3 Hyperbel
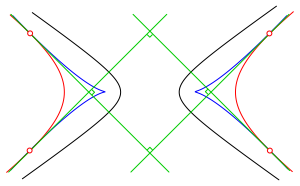
Abb. 4: Hyperbel
Die Abbildung 4 gilt fźr a > b. Was geschieht bei a = b? Was geschieht bei a < b?
4 Formeln
4.1 Parabel
Standardparabel:
![]()
Zugehšrige FrŽgier-Parabel:
![]()
Evolute der Standardparabel:
![]()
4.2 Ellipse
Ellipse mit den Halbachsen a und b:
![]()
Verkleinerungsfaktor f fźr die FrŽgier-Ellipse:
![]()
Evolute der Ellipse:
![]()
Was folgt fźr den Sonderfall des Kreises?
4.3 Hyperbel
Hyperbel mit den Halbachsen a und b:
![]()
Streckungsfaktor f fźr die FrŽgier-Hyperbel:
![]()
Evolute der Hyperbel:
![]()
Was folgt fźr den Sonderfall der gleichseitigen Hyperbel?
Literatur
Weiss, Gunter (2018): Thales-3D mit der Idee von M. FrŽgier. IBDG, InformationsblŠtter der Geometrie. 37. 2/2018. 30-37