Hans Walser, [20090625c]
Fibonacci-Trapeze
Anregung: [Deshpande
2009]
1 Hexagon mit angesetzten Quadraten
1.1
Basisfigur
Wir basieren unsere
berlegungen auf folgender Figur. Einem zentralen Hexagon werden Quadrate
angesetzt.
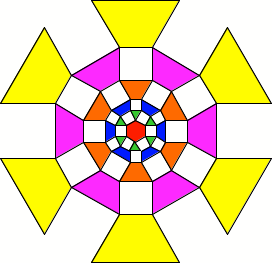
Hexagon mit aufgesetzten
Quadraten
Die Trapeze sind
offensichtlich gleichschenklig und haben die Basiswinkel 60¡. Sind sie auch
hnlich?
1.2
Analyse der Trapeze
Wir interpretieren das
grne Dreieck mit etwas Gewalt als Trapez. Es hat die Unterkante 1, die
Schenkel 1 und die Oberkante 0.
Bei den Trapezen
bezeichnen wir die lngere Parallelseite als Unterkante, die krzere als Oberkante.
Wir knnen die Trapeze ma§getreu in einen Dreiecksraster einzeichnen.

Trapeze im
Dreiecksraster
Die Trapeze sind
offensichtlich nicht hnlich.
Es gilt:
|
Ring Nr. |
Farbe |
Oberkante |
Schenkel |
Unterkante |
|
0 |
grn |
0 |
1 |
1 |
|
1 |
blau |
1 |
1 |
2 |
|
2 |
orange |
1 |
2 |
3 |
|
3 |
magenta |
2 |
3 |
5 |
|
4 |
gelb |
3 |
5 |
8 |
Das riecht nach
Fibonacci.
Die Trapeze im Ring Nr.
n haben die Oberkante ![]() , die Schenkel
, die Schenkel ![]() und
die Unterkante
und
die Unterkante ![]() .
.
1.3
Induktionsbeweis
Aussage fr ![]() (blaue Trapeze)
richtig.
(blaue Trapeze)
richtig.
Aussage sei richtig bis
und mit Ring Nr. n (Beweisfigur, u§erer
hellgrner Ring).
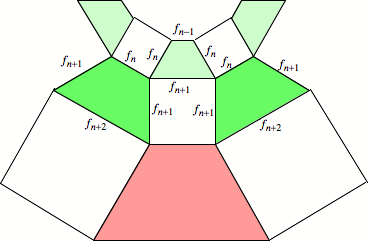
Beweisfigur
Ein Trapez im Ring Nr. ![]() hat dann die
Oberkante
hat dann die
Oberkante ![]() (Quadrat der
Seitenlnge
(Quadrat der
Seitenlnge ![]() ) und die Schenkel
) und die Schenkel ![]() (Quadrate der
Seitenlnge
(Quadrate der
Seitenlnge ![]() ). Fr die Unterkante zerlegen wir gem§ Figur in ein
Parallelogramm und ein Dreieck.
). Fr die Unterkante zerlegen wir gem§ Figur in ein
Parallelogramm und ein Dreieck.
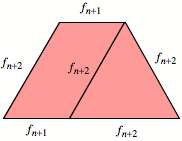
Zerlegung
Die Unterkante hat also
die Lnge ![]() .
.
1.4
Goldenes Trapez
Wenn wir die
Konstruktion nach au§en weiterfhren, nehmen die Trapeze immer mehr die Form an
eines Trapezes mit der Oberkante ![]() , der Schenkel 1 und der Unterkante
, der Schenkel 1 und der Unterkante ![]() . Dabei ist
. Dabei ist ![]() und
und ![]() (goldener
Schnitt). Dieses Trapez nennen wir daher das goldene Trapez. Die Basiswinkel des goldenen Trapezes sind 60¡.
(goldener
Schnitt). Dieses Trapez nennen wir daher das goldene Trapez. Die Basiswinkel des goldenen Trapezes sind 60¡.
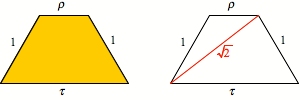
Goldenes Trapez
Das goldene Trapez hat
eine bemerkenswerte Eigenschaft: Seine Diagonale hat exakt die Lnge ![]() . Das kann mit dem Kosinussatz nachgewiesen werden.
. Das kann mit dem Kosinussatz nachgewiesen werden.
Wir knnen also sechs
goldene Trapeze im Wechsel mit sechs Einheitsquadraten zu einem Ring zusammenfgen,
wobei alle Diagonalen gleich lang sind.
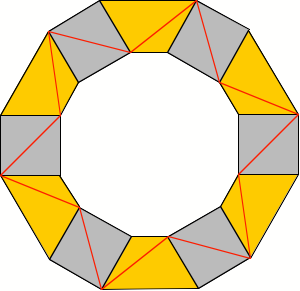
Ring mit gleich langen
Diagonalen
In den
Fibonacci-Trapezen ist die Diagonale natrlich nur nherungsweise das ![]() der
Schenkellnge. Im Trapez
der
Schenkellnge. Im Trapez ![]() hat die
Diagonale
hat die
Diagonale ![]() die Lnge:
die Lnge:
![]()
Somit ist:
![]()
Direkter Beweis:
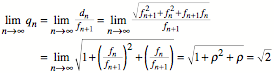
Tabelle:
q[1] = 1.322875656
q[2] =
1.452966315
q[3] = 1.4
q[4] =
1.419727086
q[5] =
1.412119981
q[6] =
1.415015044
q[7] =
1.413907687
q[8] =
1.414330435
q[9] =
1.414168927
q[10] = 1.414230612
q[11] = 1.41420705
q[12] = 1.41421605
q[13] = 1.414212612
q[14] = 1.414213925
q[15] = 1.414213424
q[16] = 1.414213615
q[17] = 1.414213542
q[18] = 1.41421357
q[19] = 1.414213559
q[20] = 1.414213564
q[21] = 1.414213562
q[22] = 1.414213563
q[23] = 1.414213562
q[24] = 1.414213562
Bemerkenswert ist das
schne rationale Zwischenresultat ![]() .
.
1.5
Eine Spirale
Wir knnen die Trapeze
im Dreiecksraster zu einer Spirale zusammenfgen.
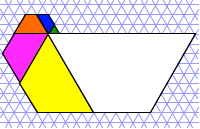
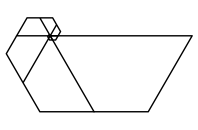
Spirale aus
Fibonacci-Trapezen
Die Eckpunkte liegen im
Grenzfall auf einer logarithmischen Spirale. Rechts sind die Trapeze von 0 bis
29 gezeichnet.
1.6
Flcheninhalt
Das Trapez ![]() im ring Nr. n hat den Flcheninhalt:
im ring Nr. n hat den Flcheninhalt:
![]()
Insbesondere hat das
grne Dreieck, also ![]() , den Flcheninhalt
, den Flcheninhalt ![]() . Wir nehmen diesen Flcheninhalt als Vergleichsma§ und erhalten
so fr das Trapez
. Wir nehmen diesen Flcheninhalt als Vergleichsma§ und erhalten
so fr das Trapez ![]() den relativen
Flcheninhalt:
den relativen
Flcheninhalt:
![]()
Tabellarisch sieht das
so aus:
psi(t[0]) = 1
psi(t[1]) = 3
psi(t[2]) = 8
psi(t[3]) = 21
psi(t[4]) = 55
psi(t[5]) = 144
psi(t[6]) = 377
psi(t[7]) = 987
psi(t[8]) = 2584
psi(t[9]) = 6765
psi(t[10])
= 17711
Zum Vergleich:
f[2*(0+1)] = 1
f[2*(1+1)] = 3
f[2*(2+1)] = 8
f[2*(3+1)] = 21
f[2*(4+1)] = 55
f[2*(5+1)] = 144
f[2*(6+1)] = 377
f[2*(7+1)] = 987
f[2*(8+1)] = 2584
f[2*(9+1)] = 6765
f[2*(10+1)]
= 17711
Offenbar gilt die
Identitt:
![]()
Der Beweis geht ber
die Formel von Binet.
2
Andere Vielecke im Zentrum
2.1
Dreieck im Zentrum
2.1.1
Regulres Dreieck im Zentrum
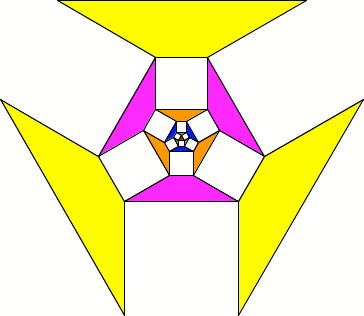
Regulres Dreieck im
Zentrum
Die gleichschenkligen
Trapeze haben nun Basiswinkel 30¡. Es gilt:
|
Ring Nr. |
Farbe |
Oberkante |
Schenkel |
Unterkante |
Relative Flche |
|
0 |
grn |
0 |
1 |
|
1 (Einheit) |
|
1 |
blau |
1 |
|
4 |
5 |
|
2 |
orange |
|
4 |
|
24 |
|
3 |
magenta |
4 |
|
19 |
115 |
|
4 |
gelb |
|
19 |
|
551 |
Es gilt die Rekursion:
![]()
Weiter ist:
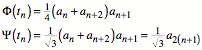
Es gilt die Rekursion:
![]()
Die Spirale wchst
happig:
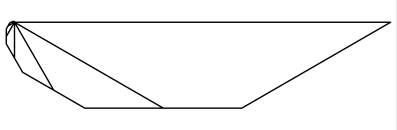
Spirale
2.1.2
Beliebiges Dreieck im Zentrum
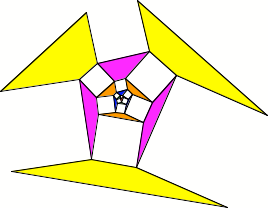
Beliebiges Dreieck im
Zentrum
Wir haben immer noch
Trapeze, aber keine gleichschenkligen mehr. Das Experiment (Cabri) zeigt, dass
die Flchenrelationen noch stimmen:
|
Ring Nr. n |
Farbe |
Relative Flche |
|
0 |
grn |
1 (Einheit) |
|
1 |
blau |
5 |
|
2 |
orange |
24 |
|
3 |
magenta |
115 |
|
4 |
gelb |
551 |
Fr den Fall ![]() gibt [Deshpande
2009] einen proof without words. Fr den allgemeinen Fall habe ich keinen
Beweis.
gibt [Deshpande
2009] einen proof without words. Fr den allgemeinen Fall habe ich keinen
Beweis.
Spiralen gibt es auch hier, sogar drei Stck. Wir whlen aus der Figur eine geeignete Folge von Trapezen aus (geht auf drei Arten), die wir dann ãeinrollenÒ.
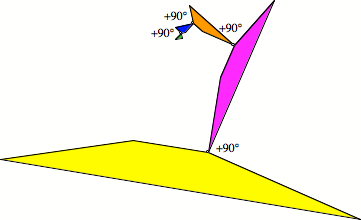
Auswahl von Trapezen

Spirale
2.2
Viereck im Zentrum
2.2.1
Quadrat im Zentrum
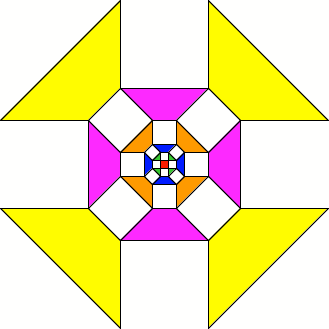
Quadrat im Zentrum
Die gleichschenkligen
Trapeze haben nun Basiswinkel 45¡. Es gilt:
|
Ring Nr. |
Farbe |
Oberkante |
Schenkel |
Unterkante |
Relative Flche |
|
0 |
grn |
0 |
1 |
|
1 (Einheit) |
|
1 |
blau |
1 |
|
3 |
4 |
|
2 |
orange |
|
3 |
|
15 |
|
3 |
magenta |
3 |
|
11 |
56 |
|
4 |
gelb |
|
11 |
|
209 |
Es gilt die Rekursion:
![]()
Weiter ist:
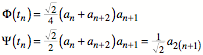
Es gilt die Rekursion:
![]()
Die Spirale wchst:
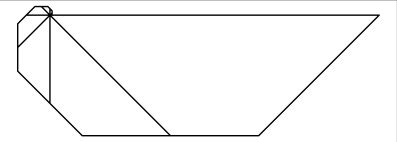
Spirale
2.2.2
Parallelogramm im Zentrum
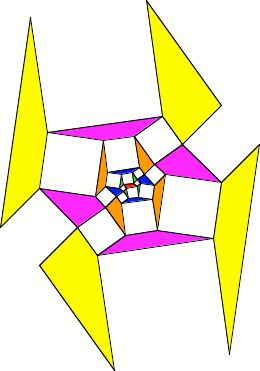
Parallelogramm im
Zentrum
Mit einem
Parallelogramm geht es aber.
|
Ring Nr. |
Farbe |
Relative Flche |
|
0 |
grn |
1 (Einheit) |
|
1 |
blau |
4 |
|
2 |
orange |
15 |
|
3 |
magenta |
56 |
|
4 |
gelb |
209 |
Beweis?
Mit einem allgemeinen
Viereck im Zentrum geht es nicht; die Trapeze in einem Ring sind nicht mehr
flchengleich. Das Dreieck ist ein Sonderfall.
Vermutlich funktioniert
es allgemein fr affinregulre Vielecke.
Literatur
[Deshpande 2009] Deshpande,
M. N. : Proof Without Words: Beyond Extriangles. MATHEMATICS MAGAZINE. Vol. 82,
No. 3, June 2009, p. 208.