1 Worum geht es?

Einfache Vorgaben über die Scheitelkrümmungskreise führen zu Ellipsen mit dem Achsenverhältnis . Sie können daher in DIN-Rechtecke eingepasst werden. Beweise durch Überlegen und/oder Nachrechnen.

Über DIN-Rechtecke siehe Walser (2013).

2 Krümmungskreise in den spitzen Scheiteln

Wir beginnen mit zwei gleich großen sich berührenden Kreisen (Abb. 1a).

Abb. 1: Zwei sich berührende Kreise

In der Abbildung 1b ist die Ellipse eingezeichnet, welche diese beiden Kreise umfasst und in den spitzen Scheiteln als Krümmungskreise (kissing circles) hat.

Diese Ellipse passt in ein DIN-Rechteck (Abb. 2a). Sie hat das Achsenverhältnis:

(1)

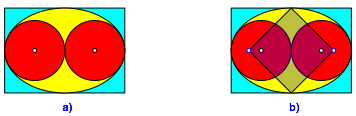
Abb. 2: DIN-Rechteck. Brennpunkte

Die Brennpunkte der Ellipse finden wir durch Einpassen eines auf der Spitze stehenden Quadrates (Abb. 2b).

In der Abbildung 3 ist zusätzlich die Evolute der Ellipse eingezeichnet.

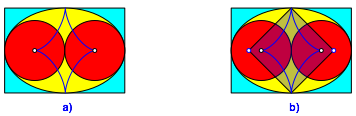
Abb. 3: Evolute

3 Krümmungskreise in den stumpfen Scheiteln

Wir beginnen mit zwei gleich großen Kreisen, von denen jeder den Mittelpunkt auf der Kreislinie des anderen hat (Abb. 4a). Diese Kreiskonfiguration kann als Start einer Konstruktion eines gleichseitigen Dreiecks oder eines regelmäßigen Sechsecks gesehen werden. Zahlenmäßig denken wir dabei an , was zunächst nichts mit dem des DIN-Formates zu tun hat.

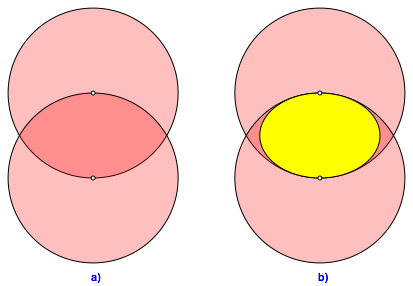
Abb. 4: Zwei große Kreise

In das Auge, also den Überlappungsbereich der beiden Kreise zeichnen wir die Ellipse mit den beiden Kreisen als Krümmungskreise in den stumpfen Scheiteln (Abb. 4b). Diese Ellipse lässt sich wiederum in ein DIN-Rechteck einpassen (Abb. 5a). Sie hat ebenfalls das Achsenverhältnis:

(2)

Sie hat also dieselbe Form wie die Ellipse in der Abbildung 1b.

Die Brennpunkte finden wir durch geeignete Quadratdiagonalen (Abb. 5b). Diese Diagonalen verlaufen auch durch die Schnittpunkte der Kreise mit den Rechteckseiten (rot in Abb. 5b).

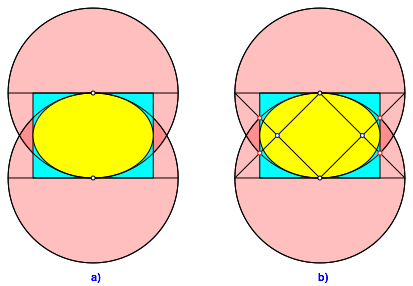
Abb. 5: Ellipse

4 Im Kreis

Zwei solche sich in stumpfen Scheiteln berührende Ellipsen passen in einen Kreis, so dass dieser Krümmungskreis in den beiden anderen stumpfen Scheiteln wird (Abb. 6a). Bei vier Ellipsen erhalten wir einen kleeblattförmigen Überlappungsbereich (Abb. 6b).

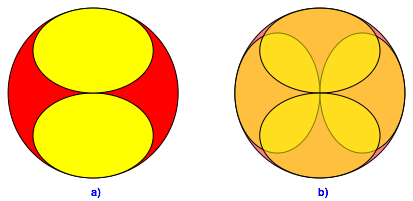
Abb. 6: Zwei und vier Ellipsen im Kreis

5 Vier Ellipsen in einer fünften

Vier Ellipsen aneinandergereiht passen in eine größere fünfte Ellipse von derselben Form (Abb. 7) und zwar so, dass die Krümmungskreise in den stumpfen Scheiteln der beiden äußersten Ellipsen gleich den Krümmungskreisen in den spitzen Scheiteln der umfassenden Ellipse ist.

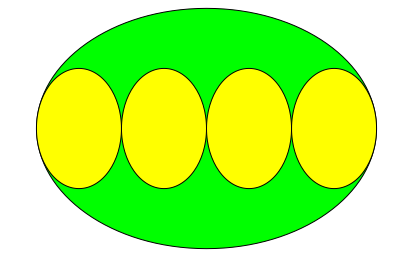
Abb. 7: Vier Ellipsen in einer fünften

Die Figur lässt sich in einen DIN-Raster einpassen (Abb. 8).

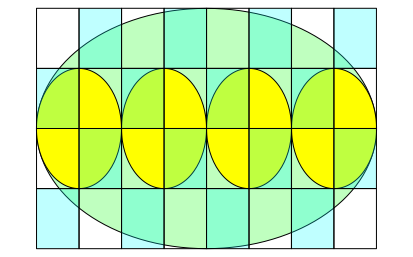
Abb. 8: Im DIN-Raster

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.