Hans Walser, [20061002a]

Dynamische Schneeflocke

1        Worum es geht

Es geht darum, die Konstruktion, welche zur Schneeflocke von Helge van Koch fŸhrt, zu dynamisieren.

2        Basiskonstruktion

Auf einer Strecke AB wŠhlen wir einen Punkt C. Wir definieren dass VerhŠltnis:

Dann zeichnen wir einen Streckenzug ACFDB so dass die Teilstrecken AC, CF, FD, DB alle gleich lang sind.

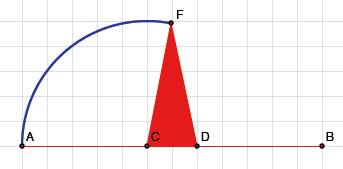
Basiskonstruktion

Nun bauen wir die Sache zum Fraktal aus.

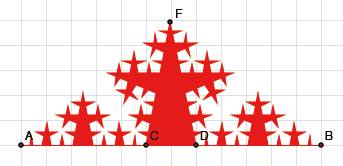
Fraktal

Nun kšnnen wir C bewegen, das hei§t, p variieren.

3        Beispiele

3.1       Schneeflocke von Helge van Koch

FŸr  ergibt sich ein Drittel des Randes der Schneeflocke von Helge van Koch. Die aufgesetzten Dreiecke sind gleichseitig.

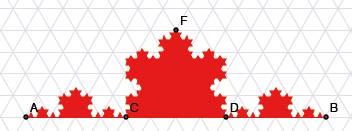
Rand der Schneeflocke

Die folgende Abbildung zeigt die Schneeflocke als Ganzes.

Schneeflocke

Diese Schneeflocke basiert auf der Sternfigur .

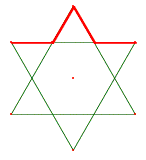
Sternfigur

3.2       Minimales p

Das minimale p ist ; in diesem Fall erhalten wir eine Strecke.

Strecke

3.3       Rechte Winkel

FŸr  erhalten wir rechtwinklig gleichschenklige Dreiecke aufgesetzt.

Halbe Quadrate aufgesetzt

Dies lŠsst sich einbauen in die Sternfigur .

Sternfigur

Wir erhalten die folgende Schneeflocke.

Schneeflocke

3.4       Im Pentagramm

FŸr  erhalten wir goldene Dreiecke aufgesetzt.

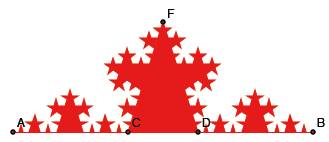
Goldene Dreiecke

Dies lŠsst sich ins Pentagramm  einbetten.

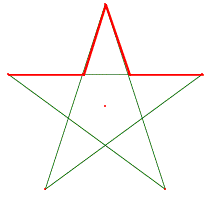
Pentagramm


Wir erhalten die folgende Schneeflocke.

Schneeflocke

3.5       MerkwŸrdiges

FŸr  sieht die Sache merkwŸrdig aus.

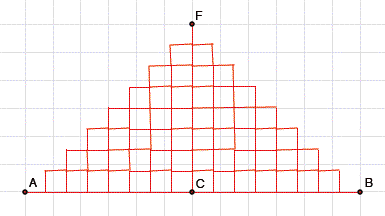
MerkwŸrdig


Das lŠsst sich in die Figur  einbetten.

Die Figur , ein simples Kreuz

Als ãSchneeflockeÒ ergibt sich ein Quadrat welches Ÿberall dicht mit Fraktallinien besetzt ist.

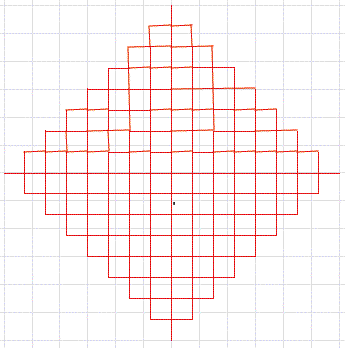
Quadrat als Schneeflocke

4        Dimension

FŸr die fraktale Dimension D der Randkurven erhalten wir:

Also:

Der Funktionsgraph von  sieht fŸr die relevanten Werte  so aus:

Funktionsgraph

FŸr  ergibt sich eine Strecke. Die fraktale Dimension ist 1. FŸr  ergibt sich ein ausgefŸlltes Quadrat; die fraktale Dimension ist 2. FŸr  ergeben sich Schneeflocken. Die fraktalen Dimensionen ihrer RŠnder liegen zwischen 1 und 2.

5        Sternfiguren

Wir haben die verallgemeinerten Schneeflocken durch Einbau in eine Sternfigur  gefunden. Wie hŠngen p und D von n ab?

Wir setzen im Folgenden  voraus.

Der Zentriwinkel  eines regelmŠ§igen n-Eckes ist . Wenn wir nun die Sternfigur  in den Einheitskreis einzeichnen, erhalten wir:

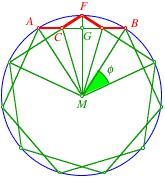
Sternfigur

Es ist dann:

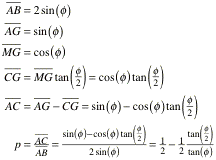
Wegen

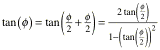
erhalten wir:

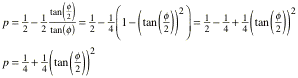
Wegen  ergibt sich:

Daraus ergibt sich fŸr D:

Die Figur zeigt den Funktionsgraphen fŸr .

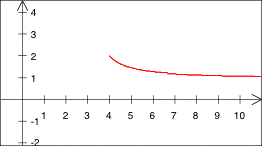
Insbesondere ist  und . FŸr  wird das Fraktal zum Umkreis.