Hans Walser, [20120107]

Dritteln durch Halbieren

Anregungen: B. J., B. und J. W., R.

Es werden verschiedene Beispiele vorgestellt, bei denen wir durch fortgesetztes Halbieren zu Dritteln kommen.

1 Farbenmauer

Die Farbenanteile eines Steins sind gleich wie die Farbenanteile der beiden darunter liegenden Steine. Wir müssen also die Farbanteile dieser beiden Steine zusammenzählen und dann halbieren.

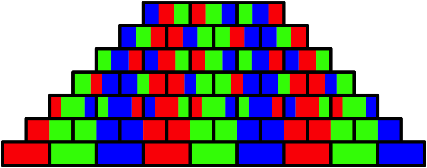
Farbenmauer

Zuunterst haben wir einfarbige Steine, gegen oben werden sie immer mehr zu Trikoloren. Stimmt das mit der Trikolore?

2 Geometrische Reihe

Aus der Halbierungsfolge wählen wir jedes zweite Folgenglied aus, also die geometrische Folge , und addieren. Demo mit Excel:

n	(1/4)^n	Summe
1	0.250000	0.250000
2	0.062500	0.312500
3	0.015625	0.328125
4	0.003906	0.332031
5	0.000977	0.333008
6	0.000244	0.333252
7	0.000061	0.333313
8	0.000015	0.333328
9	0.000004	0.333332
10	0.000001	0.333333

Die Summe konvergiert gegen einen Drittel. Das ist natürlich ein alter Hut:

Fragen:

· Wie hängt das mit dem Dualsystem zusammen?

· Wie mit dem Zahlensystem zur Basis 4?

3 Dritteln einer Strecke

Um eine Strecke zu dritteln, können wir einen beliebigen Startpunkt außerhalb der Geraden PQ wählen. Den Mittelpunkt der Strecke nennen wir , den Mittelpunkt der Strecke nennen wir und so weiter. Wir haben also folgende Rekursion:

Die Abbildung zeigt die ersten Schritte.

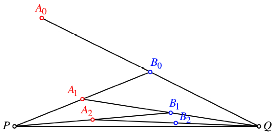
Dritteln einer Strecke?

Wir vermuten, dass die beiden Punktfolgen je einen Lines beziehungsweise haben und dass A der erste und B der zweite Drittelspunkt der Strecke PQ ist.

Bemerkungen und Fragen:

· Warum ist das so?

· Tatsächlich brauchen wir nur ganz wenige Punkte der Punktfolge zu konstruieren und finden dann sehr leicht die Drittelspunkte. Wie geht diese Minimalkonstruktion?

· Was geschieht, wenn wir den Startpunkt auf der Geraden PQ wählen?

4 Dritteln eines Papierstreifens

Wir falten einen Streifen der in der Mitte. Die Faltlinie markieren wir mit rot. Nun falten wir von rechts her bis zur roten Faltlinie und markieren die neue Faltlinie blau. Anschließend von links her bis zur blauen Faltlinie, die neue Faltlinie markieren wir wieder rot. Nun von rechts her bis zur neuen roten Faltlinie, gibt eine neue blaue Faltlinie. Und so weiter. Die Abbildung illustriert das schrittweise Vorgehen.

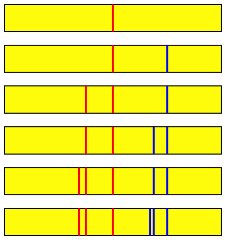
Falten des Streifens

Wir vermuten, dass die roten Faltlinien gegen das linke Drittel und die blauen gegen das rechte Drittel des Streifens konvergieren.

Um das einzusehen, skalieren den Streifen am linken Ende mit 0 und am rechen Ende mit 1. Weiter sei die Position der roten Faltlinien, also , und die Position der blauen Faltlinien. Es ist . Damit gilt die Rekursion:

Mit Excel ergibt sich:

n	a[n]	b[n]
0	0.500000	0.750000
1	0.375000	0.687500
2	0.343750	0.671875
3	0.335938	0.667969
4	0.333984	0.666992
5	0.333496	0.666748
6	0.333374	0.666687
7	0.333344	0.666672
8	0.333336	0.666668
9	0.333334	0.666667
10	0.333333	0.666667

Positionen der Faltlinien

Wir vermuten:

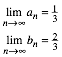
In der Tabelle erkennen wir gewöhnliche Brüche:

n
0
1
2
3

Brüche

Sehen wir eine Gesetzmäßigkeit? — Nenner vervierfachen, Zähler vervierfachen minus 1.

Bemerkungen:

· Wenn wir im Abschnitt 3 (Dritteln einer Strecke) den Startpunkt in der Mitte der Strecke PQ wählen, haben wir genau unser Streifenfaltproblem.

· Beim Streifenfalten braucht die erste Faltlinie nicht in der Mitte zu liegen. Wir können mit einem beliebigen starten.

5 Winkeldrittelung

Ein Winkel kann nicht mit Zirkel und Lineal gedrittelt werden. Hingegen können wir einen Winkelsektor analog zu unserem Streifen falten.

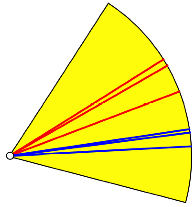
Sektor falten

6 Dritteln einer Zahl

Wir möchten die Zahl d mit Halbieren durch drei dividieren. Dazu können wir wie folgt vorgehen: Wir wählen eine Startzahl und arbeiten mit der Rekursion:

Beispiel: Wir wählen und . Mit Excel erhalten wir:

c	15.000000
n	a[n]
0	7.000000
1	4.000000
2	5.500000
3	4.750000
4	5.125000
5	4.937500
6	5.031250
7	4.984375
8	5.007813
9	4.996094
10	5.001953

Dritteln einer Zahl durch geeignetes Halbieren

Die Tabelle führt zur Vermutung:

Warum funktioniert das?

Interessant ist der Fall, wieder mit dem Startwert zu bearbeiten:

c	0.000000
n	a[n]
0	7.000000
1	-3.500000
2	1.750000
3	-0.875000
4	0.437500
5	-0.218750
6	0.109375
7	-0.054688
8	0.027344
9	-0.013672
10	0.006836

Dritteln von nichts

Wir stellen fest, dass der „Fehler“ betragsmäßig mit jedem Schritt halbiert wird.

7 Gleichseitige Dreiecke in einem Papierstreifen

Vgl. [Hilton/Pedersen 1994] und [Hilton/Pedersen/Walser 2003].

Wir beginnen mit einem langen Streifen.

Dann falten wir in irgend einer Richtung nach oben.

Auffalten.

Nun falten wir nach unten, indem wir die Oberkante des Streifens an die Faltkante anlegen. Dadurch ist die neue Faltlinie die Winkelhalbierende des Winkels zwischen der alten Faltkante und der Streifenoberkante.

Auffalten.

Nach oben falten.

Auffalten.

Nach unten falten.

Auffalten.

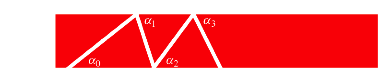
Faltprozess

Es entstehen Dreiecke, welche sich immer mehr einem gleichseitigen Dreieck annähern. Warum? — Für die im letzten Bild des Faltprozesses markierten Winkel gilt die Rekursion:

Es wird also der Winkel 180° gedrittelt. Daher werden die Dreiecke im Limes gleichseitig.

8 Zahlentripel

Wir arbeiten nun mit Zahlentripeln und verwenden die Rekursion:

Jede neue Tripelzahl ist das arithmetische Mittel der beiden anderen alten Tripelzahlen.

Für das Starttripel erhalten wir mit Excel:

n	a[n]	b[n]	c[n]
0	8.000000	5.000000	14.000000
1	9.500000	11.000000	6.500000
2	8.750000	8.000000	10.250000
3	9.125000	9.500000	8.375000
4	8.937500	8.750000	9.312500
5	9.031250	9.125000	8.843750
6	8.984375	8.937500	9.078125
7	9.007813	9.031250	8.960938
8	8.996094	8.984375	9.019531
9	9.001953	9.007813	8.990234
10	8.999023	8.996094	9.004883

Tripel mit Limes

Wir vermuten natürlich:

Das Grenztripel besteht aus den Durchschnitten der drei Startwerte. Dazu ist ein Dritteln erforderlich. In der Rekursionsformel haben wir aber nur halbiert.

8.1 Sonderfall

Für das Starttripel erhalten wir:

n	a[n]	b[n]	c[n]
0	1.000000	0.000000	0.000000
1	0.000000	0.500000	0.500000
2	0.500000	0.250000	0.250000
3	0.250000	0.375000	0.375000
4	0.375000	0.312500	0.312500
5	0.312500	0.343750	0.343750
6	0.343750	0.328125	0.328125
7	0.328125	0.335938	0.335938
8	0.335938	0.332031	0.332031
9	0.332031	0.333984	0.333984
10	0.333984	0.333008	0.333008

Sonderfall

Vermutlich ist:

In den Dezimalbrüchen zu Beginn der Tabelle erkennen wir gewöhnliche Brüche:

0	1	0	0
1	0
2
3
4
5

Brüche

Es ist manchmal sinnvoll, Brüche auf gleichen Nenner zu bringen:

0
1
2
3
4
5

Gleiche Nenner

Wir vermuten die expliziten Formeln:

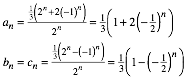
Beweis induktiv:

(I) Startwerte ok.

(II) Induktionsschritt:

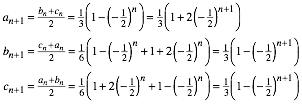
Aus den expliziten Formeln ergibt sich für sofort der Limes .

Analog erhalten wir mit den Starttripeln und den gleichen Limes .

8.2 Allgemeiner Fall

Bei einem beliebigen Starttripel arbeiten wir nun mit der Linearkombination:

Damit erhalten wir als Limes:

9 Tripel von Vektoren

Wir ersetzen nun die Zahlen durch Vektoren, also und arbeiten entsprechend mit der Rekursion:

Die Vektoren können wir als Ortsvektoren von drei Punkten deuten, welche jeweils ein Dreieck bilden. Dabei ist zum Beispiel der Mittelpunkt der Seite . Wir erhalten eine Folge von Seitenmittendreiecken. Da ein Seitenmittendreieck denselben Schwerpunkt hat wie das zugehörige Dreieck (warum ist das so?), haben alle Dreiecke denselben Schwerpunkt wie das Startdreieck .

Wir können die drei Spaltenvektoren als Matrizen zusammenfassen. Die Rekursion besteht darin, dass jede Spalte durch den Mittelwert der beiden anderen Spalten ersetzt wird.

9.1 In der Ebene

Die Abbildung zeigt das Beispiel mit den Startpunkten , , für .

Es ist dann , , . Wir sind also schon recht nahe am Schwerpunkt .

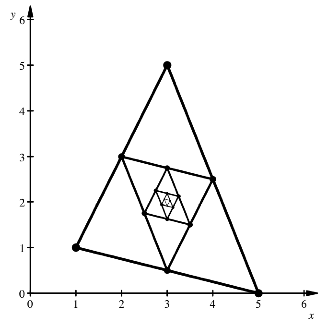
Beispiel

Die zugehörigen Matrizen haben zwei Zeilen und drei Spalten. In unserem Beispiel ist:

, und später

Für den Limes erhalten wir:

9.2 Im Raum

Drei räumliche Spaltenvektoren bilden eine .

9.2.1 Einheitsmatrix

Wenn wir mit der starten, sind die Ecken des Startdreiecks die Einheitspunkte auf den Koordinatenachsen. Das Dreieck ist gleichseitig.

Für die Matrizen erhalten wir:

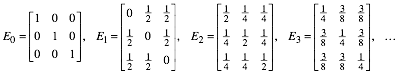
Diese Zahlen haben wir schon einmal gesehen.

Fragen und Bemerkungen:

· Bei allen Matrizen sind sämtliche Spaltensummen und Zeilensummen gleich 1. Warum?

· Was ist ?

· Behauptung: . Beweis?

Interessant sind auch die Determinanten dieser Matrizen:

Fragen und Bemerkungen:

· Wir haben doch in der Schule gelernt, dass die Determinante einer Matrix, bei der eine Spalte die Summe der beiden anderen Spalten ist, verschwindet. Unsere Determinanten sind aber (noch) nicht Null. Wo ist der Denkfehler?

· Hat etwa der Faktor beim Verkleinern der Determinante damit zu tun, dass die Seitenmittendreiecke nur einen Viertel der Fläche des Ausgangsdreieck bedecken?

· Aber Determinanten von haben doch mit Volumina zu tun?

Für den Limes erhalten wir:

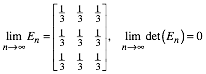
9.2.2 Der Schwerpunkt ist grau

Wir zeichnen nun den Sonderfall mit der Einheitsmatrix und verwenden gleichzeitig die Punktkoordinaten als rgb-Farbcodes (red-green-blue). Die Ecke ist dann rot, die Ecke grün und die Ecke blau.

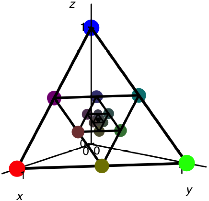
Koordinaten und rgb-Farben

Der Schwerpunkt erhält die rgb-Farbe , also ein Grau, das näher bei Schwarz als bei Weiß liegt. In der folgenden Abbildung (es ist ein 2d-Bild mit einem gleichseitigen Dreieck) ersetzen wir die Punkte durch Kreise, deren Größe wir so justieren, dass sich auf einer Seite benachbarte Kreise berühren.

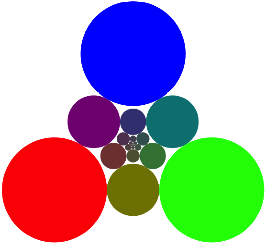
Graues Zentrum

Wie groß müssen die Kreisradien gewählt werden?

9.2.3 Aufhellung

Wir können diese triste Welt mit grauem Zentrum etwas aufhellen, indem wir die Farbtripel linear so normieren, dass der größte Wert auf 1 gesetzt wird, also:

Das sieht dann so aus:

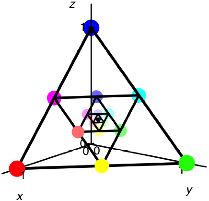
Aufhellen der Farben

Der Schwerpunkt wird nun weiß. Die folgende Abbildung zeigt das entsprechende 2d-Bild mit Kreisen.

Weißes Zentrum

Frage: Was geschieht, wenn wir auch die Koordinaten entsprechend „aufhellen“? — Die Punkte werden vom Ursprung aus auf den Einheitswürfel projiziert.

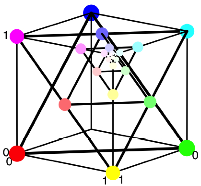
Projektion auf Einheitswürfel

9.2.4 Allgemeiner Fall

Für eine beliebige Startmatrix

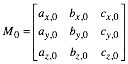
erhalten wir:

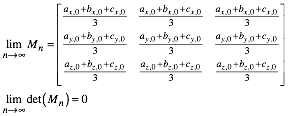
Die Abbildung zeigt die Situation für die Startmatrix:

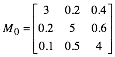
Dabei wurden die „aufgehellten“ Farben mit den Kennfarben rot, grün, blau in den Eckpunkten des Startdreiecks übernommen.

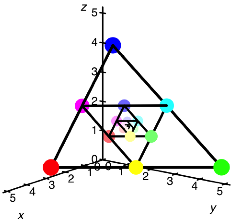
Allgemeines Beispiel im Raum

Bemerkung: Es ist . Das Ausmitteln der Spalten ist also im Wesentlichen in den Matrizen enthalten.

10 Mittelpunkte von Dreiecksbogen. Ausgleichen eines Dreiecks

Wir setzen den Punkt nun nicht mehr in die Mittel der Strecke , sondern in die Mitte desjenigen Umkreisbogens , der auch den Punkt enthält, und entsprechend für und . Wir halbieren also Kreisbogen. Die Abbildung zeigt den ersten Schritt.

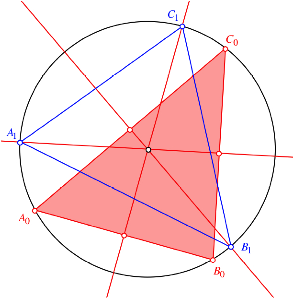
Erster Schritt

Wir schneiden die Mittelsenkrechten mit dem Umkreis.

Die folgende Abbildung zeigt die ersten drei Schritte. Das Startdreieck ist rot, und dann gilt das romantische Prinzip: Je blauer, um so näher am Unendlichen.

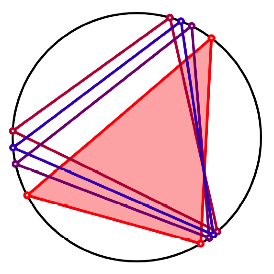
Die ersten drei Schritte

Wenn wir 10 Schritte tun, wird es schon deutlicher: Die Sache stabilisiert sich. Das Grenzdreieck ist vermutlich gleichseitig.

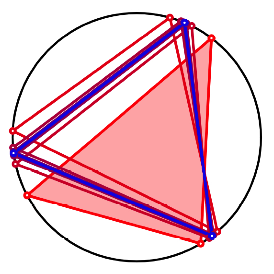
Grenzdreieck gleichseitig

Fragen:

· Warum ist das so?

· Wie hängt die Position des Grenzdreiecks vom Startdreieck ab?

· Wie „merkt“ der Computer, welcher der beiden Kreisbogen jeweils der richtige ist?

· Wo wird nun gedrittelt?

Literatur

[Hilton/Pedersen 1994] Hilton, Peter / Pedersen, Jean: Build Your Own Polyhedra. Menlo Park: Addison-Wesley 1994. ISBN 0-201-49096-X

[Hilton/Pedersen/Walser 2003] Hilton, Peter / Jean Pedersen / Hans Walser: Die Kunst der Mathematik. Von der handgreiflichen Geometrie zur Zahlentheorie. Dillingen: Akademie für Lehrerfortbildung und Personalführung. 2003