Hans Walser, [20170905]
Dreiecksunterteilung mit Winkelhalbierenden
Anregung: Hšlzl 2017
1 Worum geht es?
Wir unterteilen ein Dreieck mit den Ecktransversalen zum Winkelhalbierendenschnittpunkt in drei Dreiecke und iterieren den Prozess (Abb. 1).
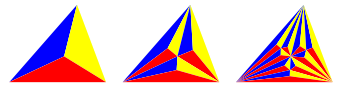
Abb. 1: Unterteilung zum Winkelhalbierendenschnittpunkt
Die Abbildung 2 zeigt die Unterteilung nach dem fźnften Iterationsschritt.
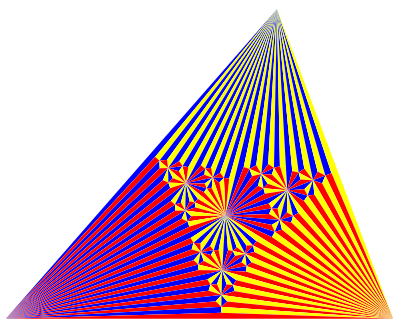
Abb. 2: Situation nach dem fźnften Schritt
2 Gleichseitiges Dreieck
Die Abbildung 3 zeigt die Unterteilung eines gleichseitigen Dreiecks nach dem fźnften Iterationsschritt.

Abb. 3: Gleichseitiges Dreieck
Die Abbildung 4 zeigt dasselbe bis zum siebten Iterationsschritt. Die Dreiecke sind mit Randlinien gezeichnet, daher die dunklere Tšnung.
Die Figur hat fraktalen Charakter.

Abb. 4: Feuerwerk
Literatur
Hšlzl, Reinhard (2017): Dreiecke in Dreiecke zerlegen. Welche Eigenschaften und ZusammenhŠnge findest du? mathematik lehren 201 | 2017, 12-15.
Websites
Hans Walser: Dreiecksunterteilung und Binomialverteilung (abgerufen 3.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung2/Dreiecksunterteilung2.htm
Hans Walser: Dreiecksunterteilung mit Seitenhalbierenden (abgerufen 5.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung3/Dreiecksunterteilung3.htm
Hans Walser: Dreiecksunterteilung mit Winkelhalbierenden (abgerufen 5.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung4/Dreiecksunterteilung4.htm
Hans Walser: Dreiecksunterteilung mit Schwerpunkt (abgerufen 5.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung5/Dreiecksunterteilung5.htm