Hans Walser, [20190107]
Dreiecksraster
1 Worum geht es?
Figuren im Dreiecksraster, vgl. (Walser 2011, S. 46).
2 RegulŠres Dreiecks-Punktraster
Die Abbildung 1 zeigt ein regulŠres Dreiecks-Punktraster (Ausschnitt).

Abb. 1: Dreiecks-Punktraster
3 Ganzzahlige Dreiecke
Im Raster gibt es ganzzahlige Dreiecke. Das gelbe Dreieck der Abbildung 2 hat die Seiten
![]() (1)
(1)
und den Winkel:
![]() (2)
(2)
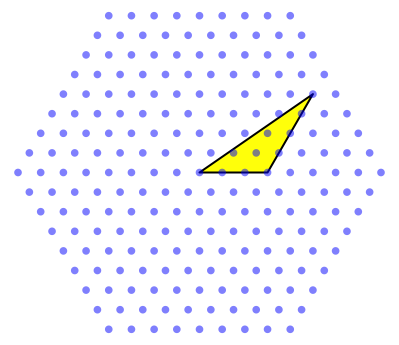
Abb. 2: Ganzzahliges Dreieck
Die
SeitenlŠngen a und b sind unmittelbar einsichtig, ebenso
der Winkel ![]() .
Zur Berechnung von c benštigen wir
den Kosinussatz:
.
Zur Berechnung von c benštigen wir
den Kosinussatz:
![]() (3)
(3)
In Beispiel des gelben Dreiecks hei§t das:
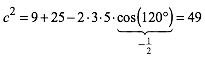 (4)
(4)
Unser Beispiel ist eine Verallgemeinerung des Begriffs pythagoreisches Dreieck. Es gibt unendliche viele solche ganzzahlige Dreiecke im Dreiecksraster.
4 †berlagerung
Im Raster der Abbildung 3 ist eine Strecke der LŠnge 7 eingetragen.

Abb. 3: Strecke der LŠnge 7
Wir drehen nun dieses Raster mitsamt der Strecke, bis diese mit der langen Seite des gelben Dreiecks der Abbildung 2 źbereinstimmt. Der Drehwinkel ergibt sich aus dem Sinussatz:
![]() (5)
(5)
Die Abbildung 4 zeigt die Situation. Die ăKathetenŇ a und b orientieren sich am blauen Punktraster, die ăHypotenuseŇ c orientiert sich am roten Punktraster.
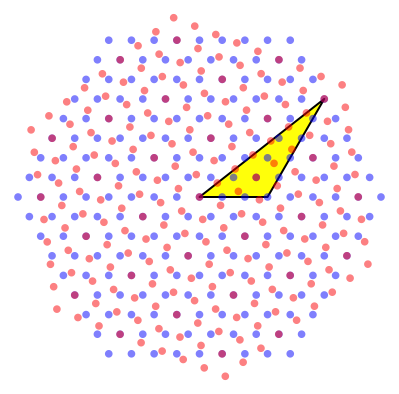
Abb. 4: †berlagerung mit Dreieck
Die
Abbildung 5 zeigt die beiden Raster ohne das konstituierende Dreieck. Es gibt
Punkte (die violetten), welche zu beiden Rastern gehšren. Diese violetten
Punkte bilden ihrerseits ein regulŠres Dreiecksraster. Es hat die Maschenweite ![]() .
Diese violetten Punkte sind die
Zentren der ăBlźmchenŇ mit blauen und roten BlźtenblŠttern. Einer dieser
violetten Punkte ist der Inkreismittelpunkt des gelben Dreiecks der Abbildung
4.
.
Diese violetten Punkte sind die
Zentren der ăBlźmchenŇ mit blauen und roten BlźtenblŠttern. Einer dieser
violetten Punkte ist der Inkreismittelpunkt des gelben Dreiecks der Abbildung
4.
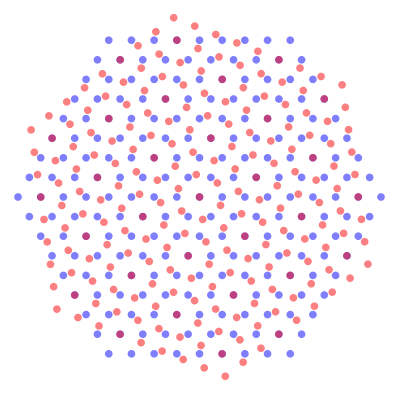
Abb. 5: †berlagerung
5 Iteration
Die Abbildung 6 zeigt eine Figur analog zur Abbildung 5, aber in den Farben orange und zyan. In grźn erscheint der †berlagerungsraster.

Abb. 6: Dasselbe in grźn
Nun źberlagern wir das violette Raster und das grźne Raster, nehmen aber die ursprźnglichen Raster (blau, rot, orange und zyan) mit. Es entsteht die Figur der Abbildung 7. Das rote und das orange Raster kommen vollstŠndig zur Deckung.

Abb. 7: †berlagerung der †berlagerungen
Es wird ein weiteres Dreiecksraster sichtbar (dunkelgrźn), nun mit der Maschenweite 7. Dies kann im rot-orangen Raster nachgezŠhlt werden.
6 Kreise
In der
Abbildung 8 sind die BlźtenblŠtter der Blźmchen der Abbildung 5 in Kreise eingebettet.
Diese Kreise bilden ein Dreiecksraster. Die Maschenweite des Rasters ist das ![]() der
Kreisradien.
der
Kreisradien.
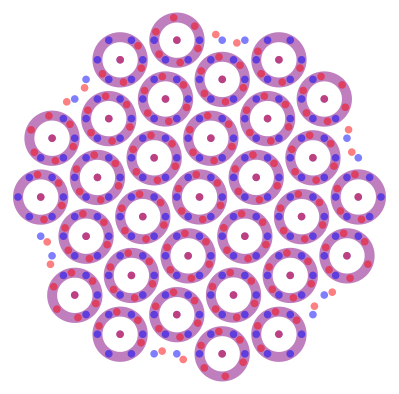
Abb. 8: Kreise durch die BlźtenblŠtter
Die Abbildung 9 zeigt nur noch die Kreise.

Abb. 9: Nur Kreise
In der Abbildung 10 wird ein zweiter entsprechender Kreisraster gemŠ§ dem Verfahren der Abbildung 7 źberlagert.

Abb. 10: †berlagerung
Es entsteht wie erwartet ein neuer Dreiecksraster. Die źbrigen Dreiecke schneiden oder berźhren sich.
In der Abbildung 11 wird das Berźhren schŠrfer dargestellt.
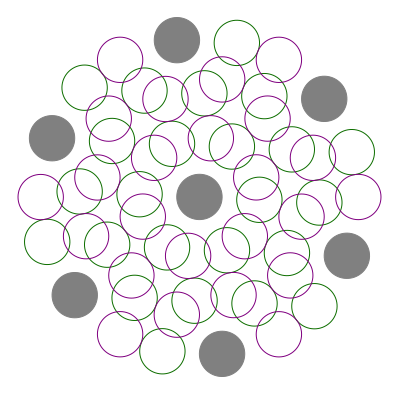
Abb. 11: Berźhrende Kreise
7 Ausblick
Analoge Spielereien kšnnen natźrlich auch mit gewšhnlichen pythagoreischen Dreiecken im Quadratraster gemacht werden (Walser 2011, S. 43)
Literatur
Walser, Hans (2011): Geometrische Miniaturen. Figuren – Muster – Symmetrien. Leipzig. EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-42-4.