Hans Walser, [20080507a]
Dreiecksketten
1 Worum es geht
Wir zeichnen eine Kette
von Dreiecken gem§ Figur. In der Figur ist ![]() . Es entsteht ein gleichseitiger Polygonzug. Wie lsst sich
das Verhalten dieses Polygonszuges beschreiben?
. Es entsteht ein gleichseitiger Polygonzug. Wie lsst sich
das Verhalten dieses Polygonszuges beschreiben?
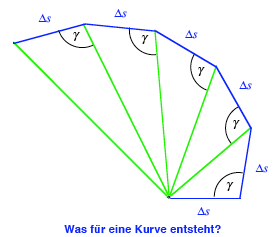
Der Verhalten des
Polygonszuges hngt wesentlich vom Winkel ![]() ab. Fr spitze
Winkel
ab. Fr spitze
Winkel ![]() ergibt sich eine
(regelm§ige) Grenzfigur, fr einen rechten Winkel
ergibt sich eine
(regelm§ige) Grenzfigur, fr einen rechten Winkel ![]() erhalten wir
eine archimedische Spirale und fr stumpfe Winkel
erhalten wir
eine archimedische Spirale und fr stumpfe Winkel ![]() eine
logarithmische Spirale.
eine
logarithmische Spirale.
2
Fallunterscheidung
2.1
Spitze Winkel
Fr spitze Winkel ![]() tendiert der
Polygonzug gegen ein gleichseitiges Sehnenvieleck mit Zentriwinkeln
tendiert der
Polygonzug gegen ein gleichseitiges Sehnenvieleck mit Zentriwinkeln ![]() . Falls
. Falls ![]() eine Teiler von
360¡ ist, ergibt sich ein regelm§iges Polygon mit Innenwinkel
eine Teiler von
360¡ ist, ergibt sich ein regelm§iges Polygon mit Innenwinkel ![]() als Grenzfigur.
Wenn
als Grenzfigur.
Wenn ![]() in einem
rationalen Verhltnis zu 360¡ steht, aber kein Teiler von 360¡ ist, erhalten
wir als Grenzfigur einen Stern, der sich aus Diagonalen gleicher Lnge eines
regelm§igen Vieleckes zusammensetzt. An den Sternspitzen haben wir ebenfalls
Innenwinkel
in einem
rationalen Verhltnis zu 360¡ steht, aber kein Teiler von 360¡ ist, erhalten
wir als Grenzfigur einen Stern, der sich aus Diagonalen gleicher Lnge eines
regelm§igen Vieleckes zusammensetzt. An den Sternspitzen haben wir ebenfalls
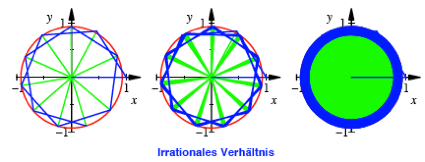
Innenwinkel ![]() . Bei irrationalem Verhltnis zu 360¡ ergibt sich ein berall
dicht belegter Kreisring.
. Bei irrationalem Verhltnis zu 360¡ ergibt sich ein berall
dicht belegter Kreisring.
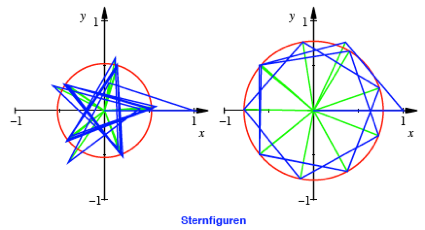
Im Folgenden einige Beispiele
mit jeweils ![]() .
.
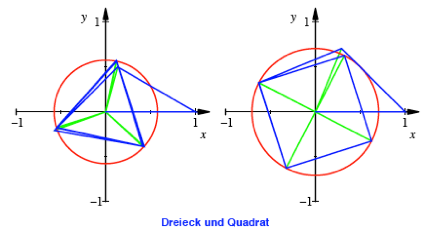
Fr ![]() oder
oder ![]() ergeben sich als
Grenzfigur ein regelm§iges Dreieck beziehungsweise ein Quadrat.
ergeben sich als
Grenzfigur ein regelm§iges Dreieck beziehungsweise ein Quadrat.
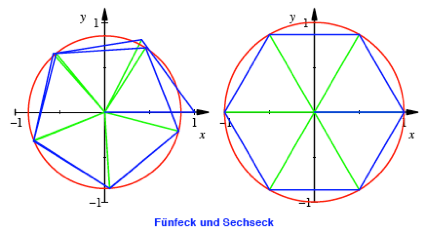
Fr ![]() erhalten wir als
Grenzfigur ein regelm§iges Fnfeck, fr
erhalten wir als
Grenzfigur ein regelm§iges Fnfeck, fr ![]() auf Anhieb das
regelm§ige Sechseck.
auf Anhieb das
regelm§ige Sechseck.
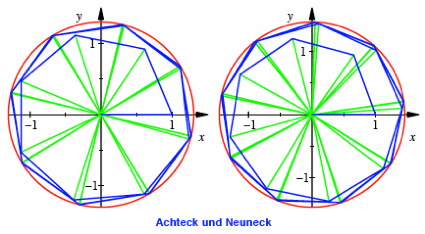
Fr ![]() und
und ![]() ergeben sich
Achteck und Neuneck.
ergeben sich
Achteck und Neuneck.
Fr ![]() ist
ist ![]() ; wir erhalten als Grenzfigur ein Pentagramm, das aus einem
regelm§igen Fnfeck durch berspringen jeder zweiten Ecke entsteht. Fr
; wir erhalten als Grenzfigur ein Pentagramm, das aus einem
regelm§igen Fnfeck durch berspringen jeder zweiten Ecke entsteht. Fr ![]() ist
ist ![]() ; wir erhalten eine Grenzfigur, welche aus einem regelm§igen
Neuneck durch berspringen jeder zweiten Ecke entsteht.
; wir erhalten eine Grenzfigur, welche aus einem regelm§igen
Neuneck durch berspringen jeder zweiten Ecke entsteht.
Wir whlen nun ![]() im Bogenma§,
also
im Bogenma§,
also ![]() . Dieser Winkel steht nicht in einem rationalen Verhltnis zu
360¡. In der folgenden Abbildung sind der Reihe nach 10, 100 und 1000 Dreiecke
gezeichnet.
. Dieser Winkel steht nicht in einem rationalen Verhltnis zu
360¡. In der folgenden Abbildung sind der Reihe nach 10, 100 und 1000 Dreiecke
gezeichnet.
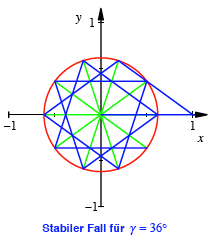
Beweisskizze: Falls
einer der grnen Radien die Lnge ![]() htte, dann auch
alle folgenden Radien. Wir htten eine Folge von gleichschenkligen Dreiecken
mit der Basis
htte, dann auch
alle folgenden Radien. Wir htten eine Folge von gleichschenkligen Dreiecken
mit der Basis ![]() und den Basiswinkeln
und den Basiswinkeln
![]() . Dies wre der stabile Fall. Dieser stabile Fall tritt exakt
ein fr
. Dies wre der stabile Fall. Dieser stabile Fall tritt exakt
ein fr ![]() oder fr
oder fr ![]() . (Gibt es
weitere stabile Flle?)
. (Gibt es
weitere stabile Flle?)
Wenn nun zum Beispiel ![]() ist, dann haben
wir im Vergleich zum stabilen Fall die Situation der Skizze:
ist, dann haben
wir im Vergleich zum stabilen Fall die Situation der Skizze:
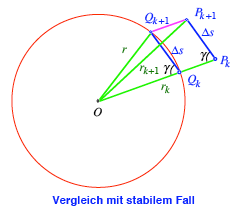
Auf Grund der
Dreiecksungleichung ist
![]()
Die folge der Radien
ist monoton fallend. Es ist sogar ![]() . Fr
. Fr ![]() erhalten wir
entsprechend eine monoton wachsende Folge von Radien.
erhalten wir
entsprechend eine monoton wachsende Folge von Radien.
Somit ist ![]() ; die Figur strebt gegen den stabilen Fall.
; die Figur strebt gegen den stabilen Fall.
2.2
Rechter Winkel
Fr ![]() entsteht eine
Figur mit aufgesetzten rechtwinkligen Dreiecken. Bei
entsteht eine
Figur mit aufgesetzten rechtwinkligen Dreiecken. Bei ![]() erhalten wir fr
die Radien die Werte
erhalten wir fr
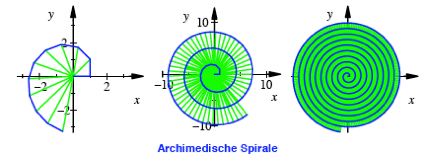
die Radien die Werte ![]() . Der Polygonzug tendiert gegen eine archimedische Spirale (vgl. [Walser 2004]).
. Der Polygonzug tendiert gegen eine archimedische Spirale (vgl. [Walser 2004]).
2.3
Stumpfer Winkel 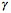
Fr ![]() erhalten wir
einen Polygonzug, der eine logarithmische Spirale als Grenzkurve hat. Dies ist nicht trivial, da die Dreiecke ja nicht
hnlich sind; wir haben keine Schneckenhaus-Situation.
erhalten wir
einen Polygonzug, der eine logarithmische Spirale als Grenzkurve hat. Dies ist nicht trivial, da die Dreiecke ja nicht
hnlich sind; wir haben keine Schneckenhaus-Situation.
Die Figurenfolge zeigt
die Situation fr ![]() und
und ![]() ; es sind 10, 100 und 1000 Dreiecke gezeichnet.
; es sind 10, 100 und 1000 Dreiecke gezeichnet.
Zum Beweis verwenden
wir die Bezeichnungen der Figur:
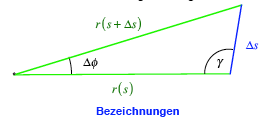
Da ![]() konstant ist,
wchst der Radius r nach au§en, und der
Winkel
konstant ist,
wchst der Radius r nach au§en, und der
Winkel ![]() geht gegen null.
ãWeit au§enÒ sind also die Radien nahezu parallel, und es gilt:
geht gegen null.
ãWeit au§enÒ sind also die Radien nahezu parallel, und es gilt:
![]()
Daraus erhalten wir:
![]()
Wir arbeiten nun
differenziell weiter:
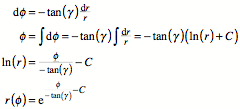
Dies ist die
Polargleichung einer logarithmischen Spirale.
Literatur
[Walser 2004] Walser, Hans: Pythagoras, eine archimedische Spirale und eine Approximation von ¹. Praxis der Mathematik (6/46), 2004, S. 287-288