Hans Walser, [20160205]

Delta-Bogenvielecke

Anregung: Renato Pandi

1     Deltakurven

Delta-Kurven sind geschlossene Kurven, welche in einem gleichseitigen Dreieck bei Drehungen einen Zwangslauf machen, indem immer alle drei Seiten des Dreiecks von der Delta-Kurve berŸhrt werden.

Abb. 1: Die Welt in der wir leben

Es werden regelmŠ§ige Bogenvielecke vorgestellt, welche als Deltakurven funktionieren. Beweise fehlen weitgehend.

2     Bildergalerie

ZunŠchst Beispiele.

Abb. 2a: Zweieck

Abb. 2b: Zweieck

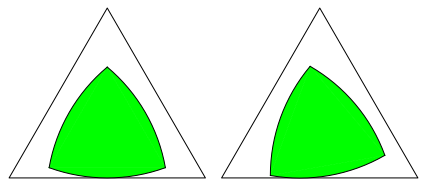
Abb. 3a: Das kannÕs wohl nicht sein

Abb. 3b: Auch das geht nicht

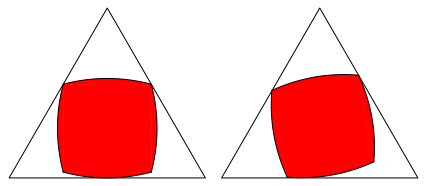
Abb. 4a: Viereck

Abb. 4b: Viereck

Abb. 5a: FŸnfeck

Abb. 5b: FŸnfeck

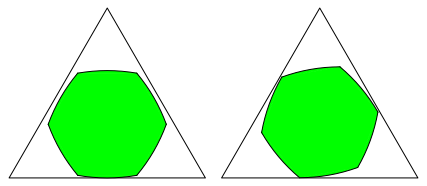
Abb. 6a: Sechseck geht nicht

Abb. 6b: Sechseck geht nicht

Abb. 7a: Siebeneck

Abb. 7b: Siebeneck

Abb. 8a: Achteck

Abb. 8b: Achteck

Abb. 9a: Neuneck geht nicht

Abb. 9b: Neuneck geht knapp nicht

Vermutung: Vielecke mit Eckenzahl  gehen nicht, die anderen schon.

3     Konstruktion und Rechnungen

Wir beschreiben die Konstruktion der Bogen-n-Ecke. Die Zeichnungen sind exemplarisch fŸr n = 5. Mit h bezeichnen wir die Hšhe des Dreieckes.

3.1    Version a

Wir zeichnen einen Bogen mit dem Radius h und dem Zentriwinkel . FŸr n = 5 sind das 24¡ (Abb. 10).

Anschlie§end fŸgen wir n = 5 solche Bšgen je um  (in unserem Beispiel also 72¡) gedreht aneinander und malen mit roter Farbe aus.

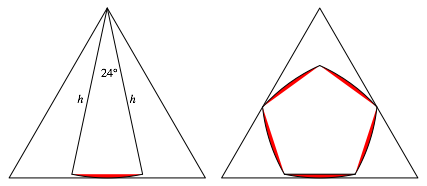
Abb. 10: Bogen und BogenfŸnfeck

Wir berechnen nun den Radius  des Au§enkreises (Umkreises) des BogenfŸnfeckes und den Radius  des Innenkreises Abb. 11).

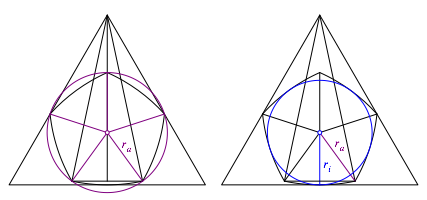
Abb. 11: Au§enkreis und Innenkreis

FŸr den Radius  des Au§enkreises finden wir:

 

                                                                                                                    (1)

 

Die Tabelle 1 zeigt die ersten numerischen Werte des Koeffizienten von h.

 

n

Koeffizient

 

n

Koeffizient

 

 

 

11

0.3373981493

2

0.5000000000

 

12

0.3367439314

3

0.3949308438

 

13

0.3362361129

4

0.3660254037

 

14

0.3358339921

5

0.3537204958

 

15

0.3355101074

6

0.3472963554

 

16

0.3352453803

7

0.3435073793

 

17

0.3350262186

8

0.3410813772

 

18

0.3348427245

9

0.3394329734

 

19

0.3346875512

10

0.3382612125

 

20

0.3345551521

Tab. 1: Koeffizienten fŸr Au§enradius

Die Werte streben zwar gegen  sind aber alle grš§er als  (Beweis sei dem Leser Ÿberlassen). Somit sind die Werte grš§er als der Inkreisradius des Dreieckes. Daraus folgt aus SymmetriegrŸnden, dass ein Bogen-n-Eck mit  nicht passen kann (Abb. 12 links fŸr n = 6).

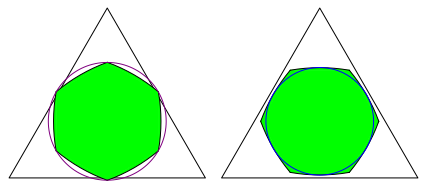
Abb. 12: Zu gro§ und zu klein

FŸr den Radius  des Innenkreises finden wir:

 

                                                                                           (2)

 

Die Tabelle 2 zeigt die ersten numerischen Werte der Koeffizienten von h.

 

n

Koeffizient

 

n

Koeffizient

 

 

 

11

0.319203076

 

 

 

12

0.321464358

3

0.137158043

 

13

0.323223011

4

0.224744871

 

14

0.324617730

5

0.264313493

 

15

0.325742457

6

0.285575220

 

16

0.326662658

7

0.298320281

 

17

0.327425089

8

0.306562965

 

18

0.328063870

9

0.312201018

 

19

0.328604366

10

0.316227426

 

20

0.329065758

Tab. 2: Koeffizienten fŸr Innenradius

Die Werte streben zwar gegen  sind aber alle kleiner als  (Beweis ?). Daraus folgt aus SymmetriegrŸnden erneut, dass ein Bogen-n-Eck mit  nicht passen kann (Abb. 12 rechts).

3.2    Version b

Wir zeichnen einen Bogen mit dem Radius  und dem Zentriwinkel . FŸr n = 5 sind das 48¡ (Abb. 13).

Anschlie§end fŸgen wir n = 5 solche Bšgen je um  (in unserem Beispiel also 72¡) gedreht aneinander und malen mit roter Farbe aus.

Abb. 13: Bogen und BogenfŸnfeck

FŸr den Radius  des Au§enkreises finden wir:

 

                                                                                                                   (3)

 

Die Tabelle 3 zeigt die ersten numerischen Werte des Koeffizienten von h.

 

n

Koeffizient

 

n

Koeffizient

 

 

 

11

0.3358703844

2

0.4330127020

 

12

0.3354625190

3

0.3711135996

 

13

0.3351458028

4

0.3535533905

 

14

0.3348949322

5

0.3459908541

 

15

0.3346928218

6

0.3420201433

 

16

0.3345275942

7

0.3396706857

 

17

0.3343907840

8

0.3381633788

 

18

0.3342762238

9

0.3371378489

 

19

0.3341793336

10

0.3364081825

 

20

0.3340966556

Tab. 3: Koeffizienten fŸr Au§enradius

Die Werte streben zwar gegen  sind aber alle grš§er als  (Beweis sei dem Leser Ÿberlassen). Somit sind die Werte grš§er als der Inkreisradius des Dreieckes. Daraus folgt aus SymmetriegrŸnden, dass ein Bogen-n-Eck mit  nicht passen kann (Abb. 14 links fŸr n = 6).

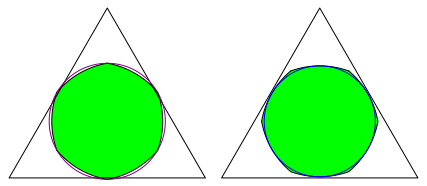
Abb. 14: Zu gro§ und zu klein

FŸr den Radius  des Innenkreises finden wir:

 

                                                                                       (4)

 

Die Tabelle 4 zeigt die ersten numerischen Werte der Koeffizienten von h.

 

n

Koeffizient

 

n

Koeffizient

 

 

 

11

0.3245293127

 

 

 

12

0.3259345620

3

0.2157104895

 

13

0.3270284208

4

0.2670370868

 

14

0.3278965185

5

0.2908386804

 

15

0.3285969554

6

0.3037942563

 

16

0.3291702788

7

0.3116173001

 

17

0.3296454810

8

0.3166997937

 

18

0.3300437376

9

0.3201867700

 

19

0.3303808049

10

0.3226822463

 

20

0.3306686041

Tab. 4: Koeffizienten fŸr Innenradius

Die Werte streben zwar gegen  sind aber alle kleiner als  (Beweis ?). Daraus folgt aus SymmetriegrŸnden erneut, dass ein Bogen-n-Eck mit  nicht passen kann (Abb. 14 rechts).

Damit haben wir bewiesen, dass Vielecke mit Eckenzahl  nicht gehen. Dass es mit Vielecken anderer Eckenzahlen immer geht, ist nicht bewiesen.