1 Three collinear points

Let a be a half circle with base b and l a line orthogonal to b (Fig. 1).

Fig. 1: Half circle and orthogonal line

We draw a circle c of arbitrary radius touching the half circle a and the line l (Fig. 2a).

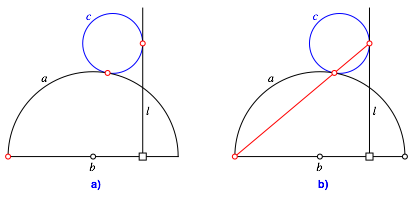
Fig. 2: A circle and three collinear points

Now the two touching points and one endpoint of the half circle are collinear (Fig. 2b).

2 Proof

The figure 3 gives a proof without words.

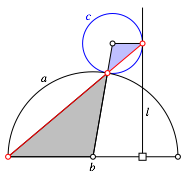
Fig. 3: Proof without words