1 About

Side faces model of the cube. The six components are made from rectangular paper with an aspect ratio of one to the square root of two (Fig. 1a). For example, a rectangle with this aspect ratio appears as a diagonal plane in the cube (Fig. 1b).

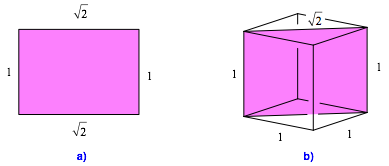
Fig. 1: One to square root of two

2 Pyramids in the cube

We can divide the cube from the center into six pyramids, the bases of which are each a side of the cube (Fig. 2). These six pyramids will be our components.

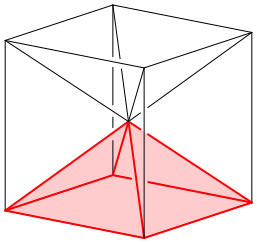
Fig. 2: Six pyramids

3 Folding a pyramid

We fold a map or a rectangular paper with the aspect ratio one to the square root of two as shown in Figure 3. Blue lines are "mountain folds", red lines are "valley folds". For the diagonal fold lines, I scratched the lines with the point of a needle on the outside (mountain fold side) before folding them.

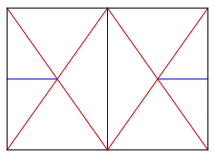
Fig. 3: Folding plan

Figure 4 shows a real example.

Fig. 4: Real example

We can fold the sheet into a pyramid. Figure 5 shows the inside of the pyramid, Figure 6 the outside. The model is temporarily fixed with paper clips.

Fig. 5: Inside of the pyramid

Fig. 6: Outside of the pyramid

4 Assembling the cube

For the cube we need six components, one for each side of the cube. We can use it to put the cube together with paper clips (Fig. 7). The inside of the pyramid comes to lie on the outside.

The side face diagonals are different. One of the side face diagonals is a fold line, the other a slit. Out of love for symmetry, we put the pieces together so that three fold lines meet at every second vertex of the cube and three slit lines at every other vertex.

Fig. 7: Assembled cube

5 Colors

Since the components are independent of one another, up to six different colors can be used (Fig. 8). In this model, glue stick was used to fix the individual pyramids and the stapler was used to assemble the six parts.

Fig. 8: Colors, glue stick and stapler, and my grandchildren's shoes

6 Moving the pyramids

The following movie shows the movement of the six pyramids.

Movie: The six pyramids

Some special cases are quite interesting.

Fig. 9.1: Starting position

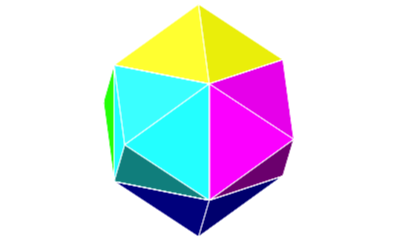
Fig. 9.2: Rhombic dodecahedron

The rhombic dodecahedron in Figure 9.2 has a cubic hole inside. The rhombic dodecahedron is a space filler. You can fill the room with rhombic dodecahedra without gaps and without overlapping.

Fig 9.3: Star

The star in Figure 9.3 is also a space filler.

Fig. 9.4: Cube

The cube is of course a space filler.

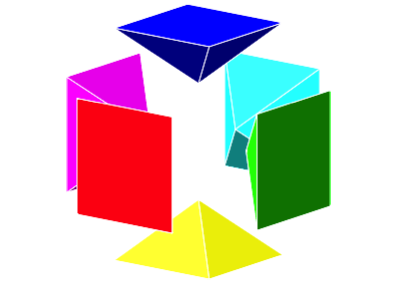
Fig. 9.5: Explosion of the cube

Websites

Hans Walser: Würfel aus sechs Bauteilen

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfel6/Wuerfel6.htm