Hans Walser, [20160533]
Chordale
Anregung: W. K., F.
1 Worum es geht
Es wird die Chordale (auch Potenzgerade oder Potenzlinie genannt) mit einigen Eigenschaften besprochen.
2 Rechnerischer Zugang
Wir wollen die Schnittpunkte zweier Kreise k1(M1(x1, y1), r1) und k2(M2(x2, y2), r2) berechnen. Sie haben die Kreisgleichungen:
![]() (1)
(1)
Subtraktion der beiden Gleichungen (1) ergibt die lineare Gleichung:
![]() (2)
(2)
Wir lsen (2) nach y auf, setzen in eine der beiden Gleichungen (1) ein und erhalten so eine quadratische Gleichung fr die x-Werte der Schnittpunkte.
Die Sache versagt, wenn die beiden Kreise konzentrisch sind.
Die durch (2) definierte Gerade hei§t Chordale der beiden Kreise k1 und k2. Die Chordale verluft durch die beiden Schnittpunkte, daher der Name.
Addition der beiden Kreisgleichungen (1) ergibt eine neue Kreisgleichung:
![]() (3)
(3)
Der zugehrige Kreis hat seinen Mittelpunkt in der Mitte der Strecke M1M2 und verluft durch die beiden Schnittpunkte.
Wie der durch (3) definierte Kreis hei§t, wei§ ich nicht.
Die Abbildung 1 zeigt ein Beispiel. Die beiden Kreise k1 und k2 sind blau, die Chordale rot und der durch (3) definierte Kreis magenta eingezeichnet.
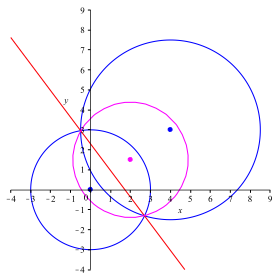
Abb. 1: Chordale
Soweit so gut. Nur haben aber zwei Kreise nicht immer zwei reelle Schnittpunkte. Die Chordale gem§ (2) existiert aber immer.
Die Abbildung 2 zeigt die Situation fr zwei berhrende Kreise. Die Chordale ist die gemeinsame Tangente.
Der Kreis gem§ (3) ist ebenfalls berhrend.
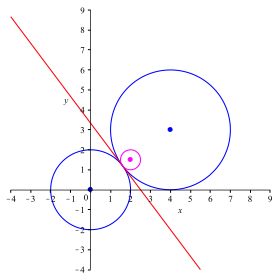
Abb. 2: Berhrende Kreise
Die Abbildung 3 zeigt die Situation mit zwei nicht schneidenden Kreisen und der zugehrigen Chordalen.
Der Kreis gem§ (3) hat einen imaginren Radius.
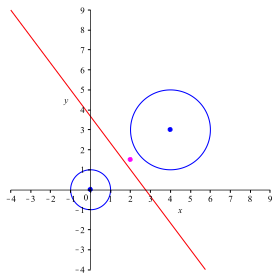
Abb. 3: Keine Schnittpunkte
3 Geometrischer Zugang
Im schneidenden und berhrenden Fall sind die Konstruktionen trivial.
Aus
Symmetriegrnden ist die Chordale senkrecht zur Geraden durch die beiden Mittelpunkte
M1 und M2.
Die Abbildung 4 illustriert eine Eigenschaft der Chordale, die dann auch im nicht schneidenden Fall angewendet werden kann. Wir zeichnen an jeden der beiden Kreise k1 und k2 eine Tangente und tragen darauf je einen gleich langen Abschnitt ab. Durch die Endpunkte der Tangentenabschnitte zeichnen wir je einen zu k1 beziehungsweise k2 konzentrischen Kreis. Diese beiden Kreise schneiden ebenfalls auf der Chordalen.

Abb. 4: Konzentrische Kreise
Im nicht schneidenden Fall knnen wir analog verfahren (Abb. 5). Wir mssen lediglich den Tangentenabschnitt ãgengend gro§Ò whlen.
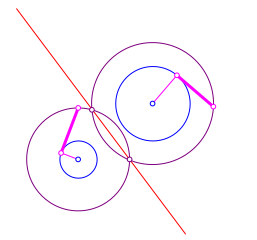
Abb. 5: Nicht schneidender Fall
Alternativ finden wir die Chordale auch durch die Mittelpunkte der Berhrungspunkte gemeinsamer Tangenten (Abb. 6).

Abb. 6: Gemeinsame Tangenten
Wenn wir von einem beliebigen Punkt der Chordale aus die Tangenten an die beiden Kreise zeichnen, ergeben sich gleich lange Tangentenabschnitte (Abb. 7). Der lila Kreis ist orthogonal zu den beiden Kreisen k1 und k2.
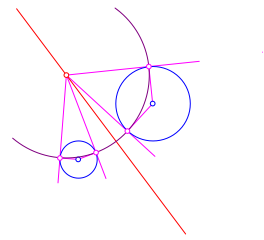
Abb. 7: Gleich lange Tangentenabschnitte