Hans Walser, [20071228e], [20131230a]

Bart des Archimedes

Anregung: [Netz/Noel 2007]

1 Worum es geht

Archimedes pflegte seine gelehrten Besucher mit der Frage zu nerven, wie groß der rote Anteil an der gesamten Kreisfläche sei.

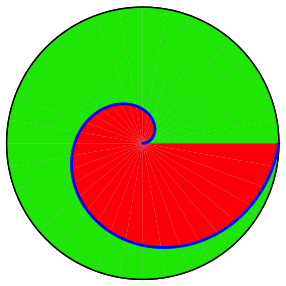
Wie groß ist der rote Anteil am Kreis?

Die blaue Trennkurve zwischen den Farben ist eine so genannte archimedische Spirale. Der Abstand vom Kreiszentrum nimmt gleichmäßig zu.

Wir können das Problem des Archimedes auf verschiedene Weisen angehen.

2 Von der Mitte aus

2.1 Radien

Wir färben die von der Mitte ausgehenden Radien rot und grün ein.

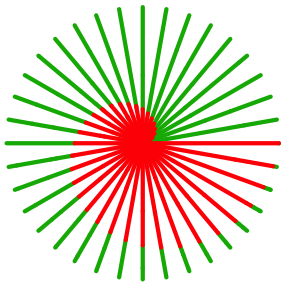
Farbige Radien

Jetzt brauchen wir nur noch den Rotanteil auf den Radien zu bestimmen. Dazu stellen wir die Radien nebeneinander. Wir sehen nochmals sehr schön, wie der Abstand vom Mittelpunkt, der Rotanteil also, gleichmäßig wächst. Die archimedische Spirale ist also so zu sagen eine aufgewickelte schräge Gerade.

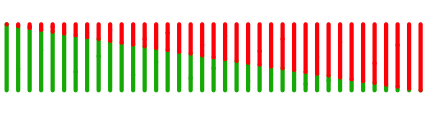
Rot-grüner Lattenzaun

Die Hälfte ist rot — das kann’s wohl nicht sein. Richtig, wir haben übersehen, dass im Kreisfächer die Zwischenräume von innen nach außen zunehmen: im Lattenzaun haben wir überall gleiche Zwischenräume.

2.2 Sektoren

Statt mit Radien müssen wir mit Sektoren arbeiten.

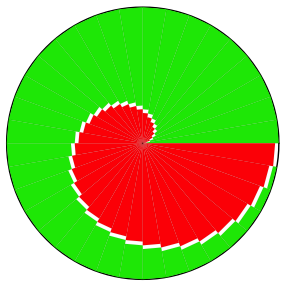
Rot-grüne Sektoren

Wenn wir die nun aufreihen, sieht das so aus:

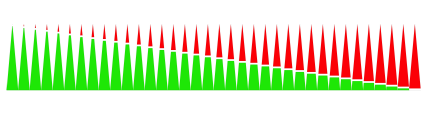
Sektoren in Reih und Glied

Wir sehen qualitativ deutlich, dass der rote Anteil weniger als die Hälfte ist.

2.2.1 Zwischenbemerkung und Sackgasse

Wir können die roten Spitzen umgekehrt in die Spalten des grünen Feldes versenken, die Spitze ganz rechts in das Loch ganz links und so weiter. Das geht schön auf, und am Schluss haben wir ein Dreieck, dessen Basislänge der Umfang des Kreises ist, also , und dessen Höhe der Kreisradius r. Somit hat das Dreieck den Flächeninhalt ; das ist — rot und grün zusammen — auch der Flächeninhalt des Kreises. Das habe wir aber eh schon in der Schule gelernt, und für die Frage des Archimedes, wie groß der Rotanteil nun wirklich ist, hilft es nicht weiter.

2.3 Der Sprung in den Raum

Wir drehen nun die Sektoren um ihre senkrechte Symmetrieachse um 90°. Ich stelle mir das vor wie stehende Lamellen, welche um die senkrechte Mittelachse drehbar sind. Solche Lamellen finden sich als Windschutz entlang von deutschen Autobahnen.

Wir verlassen damit die Ebene und haben eine räumliche Figur. Die rot-grünen Sektoren stehen wie Dominosteine hintereinander.

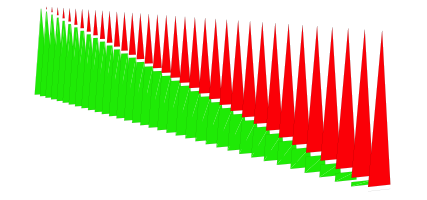
Gestaffelte Sektoren

Wir haben nun ein Dreikant-Prisma.

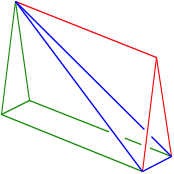
Dreikant-Prisma

Das Dreikant-Prisma ist durch eine schräge Ebene in zwei Teile geteilt, der obere, offensichtlich kleinere, Teil ist rot, der untere grün. Unsere Aufgabe besteht jetzt noch darin, den Volumenanteil des roten Teils am ganzen Dreikant-Prisma zu bestimmen.

Wenn wir das Prisma in irgend eine Richtung auseinander ziehen oder zusammenpressen (das sind so genannte affine Verzerrungen), ändern sich zwar die Volumina, nicht aber die Volumenanteile. Wir können daher das Prisma so verzerren, dass es zu einem halben Würfel wird.

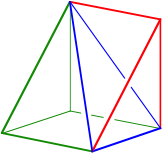
Halber Würfel

Der rote Teil ist ein unregelmäßiges Tetraeder, der restliche grüne Teil eine Pyramide, deren Spitze sich senkrecht über einer Ecke der quadratischen Grundfläche befindet. Nun zerlegen wir das Dreikant-Prisma. Zunächst entfernen wir das rote Tetraeder.

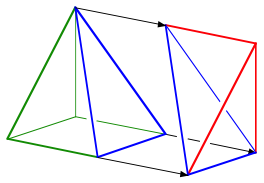
Das rote Prisma wird entfernt

Dann halbieren wir die verbleibende Pyramide durch die senkrechte Symmetrieachse. Es entstehen zwei gleichgroße symmetrische grüne Tetraeder.

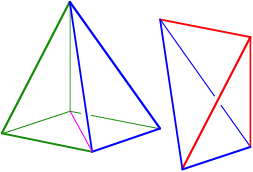
Halbierung der Pyramide

Schließlich entfernen wir noch eines der beiden grünen Tetraeder.

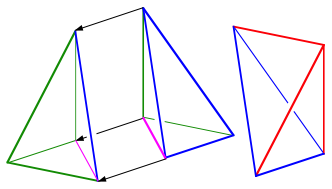
Entfernung eines grünen Tetraeders

Wenn wir das rote Tetraeder wieder zurückschieben, erkennen wir, dass es spiegelbildlich zum verbliebenen grünen Tetraeder ist.

Wir haben also drei kongruente Tetraeder; das Volumen des roten Tetraeders ist also ein Drittel des Volumens des Prismas.

Daher ist der rote Spiralflächenanteil ein Drittel der Kreisfläche.

Wir haben somit das Problem des Archimedes gelöst, ohne etwas über die Kreisfläche zu verwenden. Insbesondere brauchten wird nirgends die Kreiszahl π. Es ist auch überraschend, dass sich ein Flächenproblem über eine Volumenbetrachtung lösen lässt.

2.4 Schnittmuster

Im Anhang sind Schnittmuster für die in unseren Überlegungen verwendeten Tetraeder angegeben.

Beispiel eines Schnittmusters. Rotes Tetraeder

Das Basteln geht so: Ausschneiden und an allen Innenlinien kräftig vorfalten. Die vier satt gefärbten Dreiecke sind die Außendreiecke des Tetraeders. Die drei hell getönten funktionieren als Stecklaschen. Sie können auch kürzer geschnitten und als Klebelaschen verwendet werden.

Mit dem ersten roten und den beiden grünen Schnittmustern können die Bauteile für unsere Überlegungen gebaut werden. Mit dem zweiten roten und den beiden blauen Schnittmustern kann eine analoge spiegelbildliche Figur gebaut werden. Die beiden Figuren lassen sich zum Würfel ergänzen. Mit zwei weiteren Tetraedern kann eine Pyramide gebaut werden, deren Höhe die Hälfte der Grundkante ist.

Würfel und Pyramide

2.5 Andere archimedische Spiralen

Wenn die archimedische Spirale schneller nach außen geht, ist der rote Flächeninhalt ein Drittel der zugehörigen Kreissektorfläche.

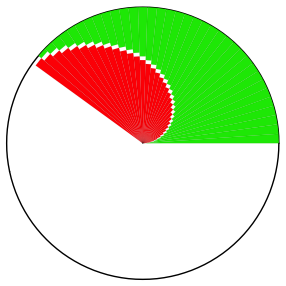
Variante

Wenn die archimedische Spirale mehr als eine Runde macht, müssen wir entsprechend mit Überlappungen arbeiten.

3 Rund geht’s

3.1 Färben mit Kreisbögen

Wir können die Fläche der archimedischen Spirale auch mit Kreisbögen färben.

Da die Zwischenräume zwischen den Bögen gleichmäßig sind, können wir die Bögen direkt zur Flächenmessung nutzen (linkes Bild). Wir stellen zunächst fest, dass die roten Bogenlängen außen und innen klein sind, in der Mitte aber groß.

Jeder Kreis ist zuerst grün und dann rot. Der Farbwechsel erfolgt proportional zum Radius des betreffenden rot-grünen Kreises. Der grüne Bogen entspricht , der rote Bogen daher . Da ein rot-grüner Kreis vom Radius den vollen Umfang hat, ist die Länge des roten Bogens darauf .

3.2 Auskämmen

Wenn wir die rot-grünen Kreise oberhalb der horizontalen blauen Linie abrasieren und alles nach unten fallen lassen, ergibt sich das rechte Bild. Die Kreisfläche wird zu einem rechtwinkligen Dreieck, dessen kurze Kathete der Kreisradius r ist und dessen lange Kathete der Kreisumfang . Die Dreiecksfläche — und damit auch die Kreisfläche — ist also .

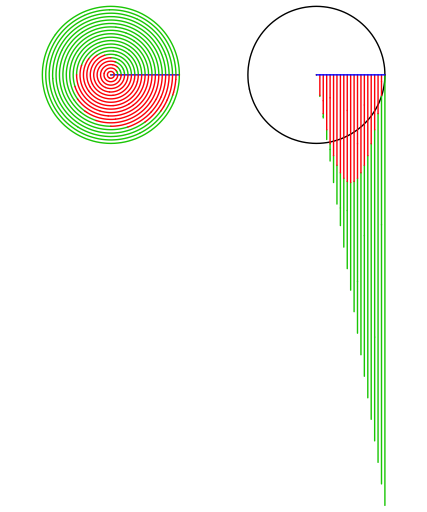
Der rote Bart im Dreieck

Uns interessiert aber der rote Bart. Sein Umriss scheint eine Parabel zu sein. Wir habe oben festgestellt, dass ein rotes Barthaar die Länge hat. Das ist tatsächlich eine quadratische Funktion in . Das längste Barthaar ist in der Mitte für ; seine Länge ist , also gerade ein Viertel des Kreisumfanges. Das können wir auch unmittelbar geometrisch einsehen: der mittlere rote Kreisbogen ist genau ein Halbkreis und hat den halten Radius wie der Kreis.

3.3 Integration wie in der Schule

Für die Bartfläche können wir jetzt handfeste Integrationsrechnung anwenden:

Das ist ein Drittel der Kreisfläche.

3.4 Geometrie

Soweit so gut. Schöner ist es geometrisch: Wir schneiden im Dreieck, das der Kreisfläche entspricht, auf halber Höhe waagerecht durch und setzen das unten abgeschnittene Teil mit Spitze nach oben links an. Dann haben wir ein Rechteck, das doppelt so hoch ist wie die Länge des längsten Barthaares (linkes Bild). Wir können auch die untere Hälfte, die rein grün ist, abschneiden (rechtes Bild).

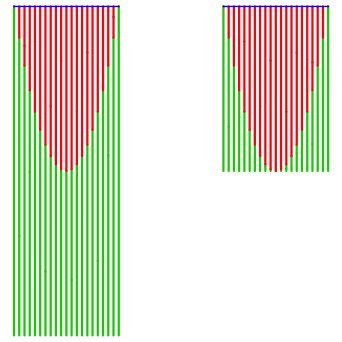
Parabel im Rechteck

Archimedes hat mit subtilen Überlegungen gezeigt, dass eine Parabelfläche, die so in ein Rechteck eingepasst werden kann wie auf dem rechten Bild, genau zwei Drittel der Rechtecksfläche ausmacht. Bezogen auf das linke Bild ist das ein Drittel der Rechtecksfläche und somit ein Drittel der Kreisfläche.

3.5 Wie groß ist π?

Vor Jahrzehnten hat mich einmal eine Schülerin während einer Klausurarbeit gefragt: „Ist es egal, was man für einsetzt?“ In unseren Überlegungen wäre es wirklich egal gewesen; der Anteil der Spiralenfläche an der Kreisfläche ist immer ein Drittel, unabhängig vom Zahlwert für π.

3.6 Der Barbier von Syrakus

Wir setzen den Bart in die Mitte und zwirbeln ihn dann hälftig links und rechts wieder auf. Der Schnurrbart bedeckt einen Drittel der Kreisfläche.

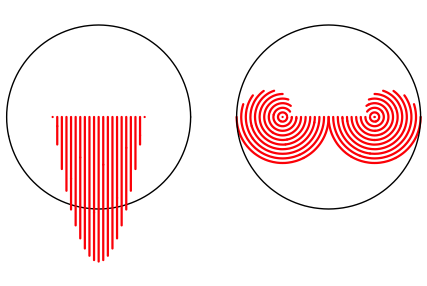
Schnurrbart

Literatur

[Netz/Noel 2007] Netz, Reviel und Noel,William: Der Kodex des Archimedes. Das berühmteste Palimpsest der Welt wird entschlüsselt. Aus dem Englischen von Thomas Filk. 2. Auflage. München: Verlag C. H. Beck 2007. ISBN 978 3 406 56336 2

Anhang: Schnittmuster für Tetraeder

Rotes Tetraeder

Spiegelbildliches rotes Tetraeder

Grünes Tetraeder

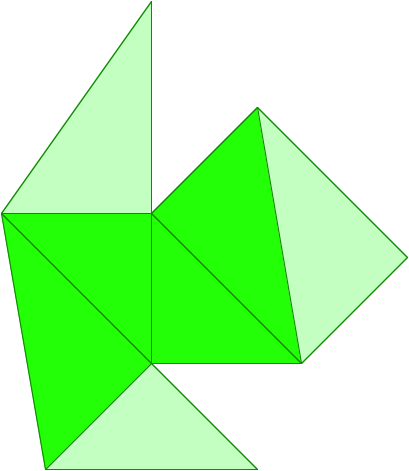
Spiegelbildliches grünes Tetraeder

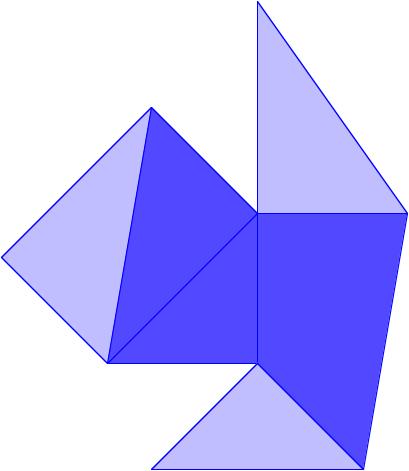
Blaues Tetraeder

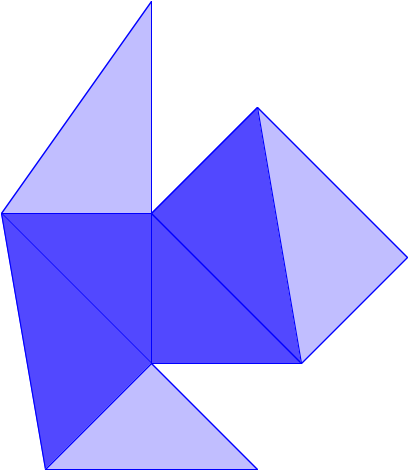
Spiegelbildliches blaues Tetraeder

Magenta Tetraeder

Spiegelbildliches magenta Tetraeder