Hans Walser, [20161015], [20180909]

Bandornamente

Anregung: Winkler (2016)

1 Worum geht es

Es werden Bandornamente als 2-reguläre Dreiecksfiguren dargestellt. Das sind Figuren, welche aus ausschließlich gleichseitigen kongruenten Dreiecken zusammengesetzt sind. Dabei kommen an jeder Dreiecksecke genau zwei Dreiecke zusammen.

2 Sieben Symmetrieklassen

Es gibt sieben Symmetrieklassen von Bandornamenten (Walser 2014, S. 80). Es werden zu jeder Symmetrieklasse Beispiele als 2-reguläre Dreiecksfigur gegeben. Zu jedem Beispiel sind in der ersten, gelb unterlegten Elementarzelle (Periode, Rapport) die Symmetrieelemente (Translationspfeil, Symmetrieachsen, Symmetriezentren) in blau eingezeichnet. Mit hellblauen Punkten sind die ungesättigten Dreiecksecken unterlegt, also diejenigen Ecken, an denen noch nicht beide dort zusammenkommenden Dreiecke gezeichnet sind. Diese Punkte sind an den Enden des gezeichneten Ausschnittes.

Die Herausforderung besteht darin, mit möglichst wenigen Dreiecken in der Elementarzelle auszukommen.

In den folgenden Abbildungen sind jeweils 4 oder 8 Elementarzellen gezeichnet.

2.1 Symmetrieklasse F₁

Die Bandornamente haben ausschließlich Translationssymmetrie.

Buchstabenbeispiel: pppp

Dem Autor hat dieses eigentlich einfachste Symmetrieverhalten am meisten Kopfzerbrechen verursacht.

Translationssymmetrie

Translationssymmetrie

Schlangenlösung

2.2 Symmetrieklasse F₂

Translationssymmetrie und Punktsymmetrie.

Buchstabenbeispiel: pdpdpdpd

Translationssymmetrie. Punktsymmetrie

Das folgende Beispiel gehört zur selben Symmetrieklasse. Es kommt mit deutlich weniger Dreiecken aus, ist dafür nicht mehr gradlinig begrenzt.

Einfacheres Beispiel ohne glatten Rand

Schlangenlösung

2.3 Symmetrieklasse F₃

Translationssymmetrie und Achsensymmetrie mit einer horizontalen Symmetrieachse. Der Translationspfeil ist auf der Symmetrieachse eingezeichnet.

Buchstabenbeispiel: cccc

Translation und Spiegelung an horizontaler Achse

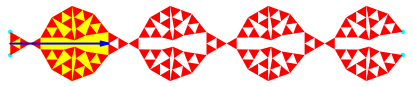
Einfacheres Beispiel

2.4 Symmetrieklasse F₄

Translationssymmetrie und Achsensymmetrie an vertikalen Symmetrieachsen.

Buchstabenbeispiel: pqpqpqpq

Translation und Spiegelungen an vertikalen Achsen

Einfacheres Beispiel ohne glatten Rand

2.5 Symmetrieklasse F₅

Translationssymmetrie, Punktsymmetrie und Achsensymmetrie an einer horizontalen und an vertikalen Achsen.

Buchstabenbeispiel: oooo

Wohl das einfachste Beispiel

Ein etwas komplizierteres Beispiel

Vgl. dazu auch Harborth 1991, Fig. 2.

2.6 Symmetrieklasse F₆

Translationssymmetrie, Punktsymmetrie und Achsensymmetrie an vertikalen Achsen.

Buchstabenbeispiel: pdbqpdbqpdbqpbbq

Translationssymmetrie, Punktsymmetrie und Spiegelung an vertikalen Achsen

Beispiel ohne glatten Rand

2.7 Symmetrieklasse F₇

Translationssymmetrie und Schubspiegelsymmetrie.

Buchstabenbeispiel: pbpbpbpb

Translationssymmetrie und Schubspiegelsymmetrie

Translationssymmetrie und Schubspiegelsymmetrie

Schlangenlösung

3 Abschluss

Bandornamente sind unendlich lang. Oben wurde immer nur ein Ausschnitt vorgestellt. An den beiden Enden sind ungesättigte Anschlusspunkte.

Solche Punkte können gesättigt werden etwa mit Figuren der folgenden Abbildung.

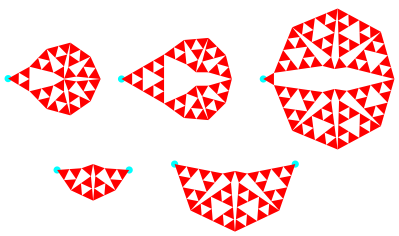
Sättigungsbeilagen

Das erste Beispiel sieht falsch aus, man meint, im innersten Punkt kämen vier Dreiecke zusammen. Die Figur ist aber korrekt, es sind zwei verschiedene Punkte. Bezogen auf die Seitenlänge 1 der Dreiecke haben die beiden Punkte den Abstand 0.0548.

Im Folgenden zwei Beispiele mit Abschluss. Selbstverständlich handelt es sich jetzt nicht mehr um Bandornamente. Wir haben nur endlich viele Dreiecke.

Abgeschlossene Figur

Abgeschlossene Figur

4 Flächenornamente

Eine analoge Klassifizierung für Flächenornamente findet sich in [1].

Literatur

Harborth, Heiko (1991): Plane four-regular graphs with vertex-to-vertex unit triangles. Discrete Mathematics 97 (1991) 219-222.

Walser, Hans (2014): Symmetrie in Raum und Zeit. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-46-2.

Winkler, Mike (2016): Ein neuer 4-regulärer Streichholzgraph. Mitteilungen der DMV 24 / 2016. 74-75.

Winkler, Mike und Dinkelacker, Peter und Vogel, Stefan (2016): New minimal (4,n)-regular matchstick graphs. arXiv:1604.07134v2

Websites

[1] Hans Walser: Flächenornamente (16.12.2016):

www.walser-h-m.ch/hans/Miniaturen/F/Flaechenornamente/Flaechenornamente.htm