Hans Walser, [20190517]
Al-Sijzī
1 Worum geht es?
Es wird ein Theorem des persischen Mathematikers Al-Sijzī (zweite Hlfte des 10. Jahrhunderts) verallgemeinert.
2 Das Theorem des Al-Sijzī
Wir
beginnen mit einer Strecke ![]() und deren
Mittelpunkt M. Um M zeichnen wir einen Kreis mit
beliebigem Radius und whlen darauf einen Punkt P. Die Abbildung 1 zeigt zwei verschiedene Wahlen des Punktes P. Den Kreis lassen wir unverndert.
und deren
Mittelpunkt M. Um M zeichnen wir einen Kreis mit
beliebigem Radius und whlen darauf einen Punkt P. Die Abbildung 1 zeigt zwei verschiedene Wahlen des Punktes P. Den Kreis lassen wir unverndert.
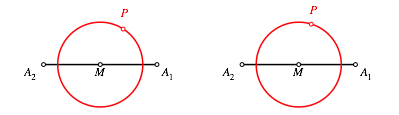
Abb. 1: Startfigur
Nun
zeichnen wir je ein Quadrat mit den Seitenlngen ![]() und
und ![]() (Abb. 2).
(Abb. 2).
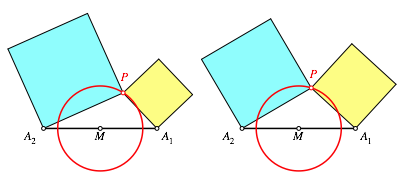
Abb. 2: Quadrate
Das Theorem des Al-Sijzī besagt nun, dass die Summe der beiden Quadratflchen eine Invariante ist, unabhngig von der Wahl des Punktes P auf dem Kreis.
Bemerkung:
Fr den Sonderfall des Kreises durch die Endpunkte der Strecke ![]() ist das
der gute alte Satz des Pythagoras. Der Satz des Pythagoras gibt allerdings
zustzlich eine Information ber die Gr§e der Summe der beiden Quadratflchen.
ist das
der gute alte Satz des Pythagoras. Der Satz des Pythagoras gibt allerdings
zustzlich eine Information ber die Gr§e der Summe der beiden Quadratflchen.
Die Abbildung 3 zeigt eine leicht modifizierte Anordnung des einen Quadrates.
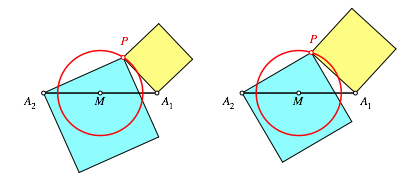
Abb. 3: Modifizierte Anordnung
Diese Modifikation erlaubt eine systematische Darstellung in der folgenden Verallgemeinerung.
3 Verallgemeinerung
Wir
interpretieren die Strecke ![]() als
Zweieck und verallgemeinern auf ein regelm§iges n-Eck (Abb. 4 fr n = 5).
als
Zweieck und verallgemeinern auf ein regelm§iges n-Eck (Abb. 4 fr n = 5).
Um den
Mittelpunkt M eines regelm§igen n-Eckes ![]() zeichnen
wir einen Kreis mit beliebigem Radius und whlen darauf einen beliebigen Punkt P. Den Kreis lassen wir im folgenden
fest, variieren aber den Punkt P.
zeichnen
wir einen Kreis mit beliebigem Radius und whlen darauf einen beliebigen Punkt P. Den Kreis lassen wir im folgenden
fest, variieren aber den Punkt P.
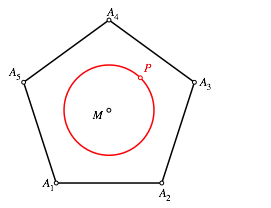
Abb. 4: Startfigur
Nun
zeichnen wir je ein Quadrat mit der Seitenlnge ![]() (Abb. 5).
(Abb. 5).
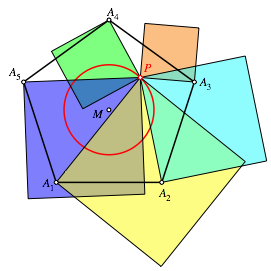
Abb. 5: Quadrate
Die Summe der Flcheninhalte dieser n Quadrate ist eine Invariante. Sie ist unabhngig von der Wahl des Punktes P auf dem als fest gedachten Kreis.
4 Beweis
Wir setzen M in den Koordinatenursprung und beschreiben das regelm§ige n-Eck durch:
![]() (1)
(1)
Weiter sei r der Radius des Kreises und:
![]() (2)
(2)
Fr die
Strecke ![]() und damit
fr die zugehrige Quadratflche ergibt sich:
und damit
fr die zugehrige Quadratflche ergibt sich:
![]() (3)
(3)
Daraus ergibt sich fr die Summe der Quadratflchen:
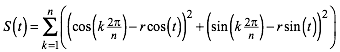 (4)
(4)
Wir haben zu zeigen, dass diese Summe unabhngig von t ist. Wir leiten nach t ab:
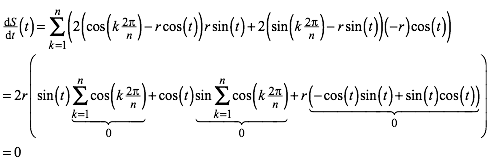 (5)
(5)
Aus (5) folgt die Invarianz.
5 Variante
Wer Lust hat, kann die in der Abbildung 6 angedeutete Variante beweisen. Bei variieren des roten Punktes auf dem roten Kreis bleibt die Quadratflchensumme invariant.
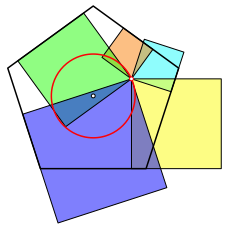
Abb. 6: Variante
6 Noch eine Verallgemeinerung
Wir ersetzen die Quadrate in der Abbildung 5 durch andere regelm§ige Vielecke, zum Beispiel durch gleichseitige Dreiecke (Abb. 7) oder regelm§ige Fnfecke (Abb. 8). Auch in diesen Fllen ist die Summe der Flcheninhalte invariant.
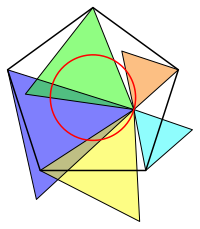
Abb. 7: Dreiecke statt Quadrate

Abb. 8: Fnfecke statt Quadrate
7 Animation
Dieser Studie ist eine GeoGebra-Animation beigegeben. Mittels Schieber knnen gewhlt werden:
á Die Eckenzahl n des regelm§igen n-Eckes.
á Die Eckenzahl m der eingefgten regelm§igen m-Ecke, deren Flchensumme invariant ist. Diese regelm§igen m-Ecke sind alle in transparentem Blau gegeben.
á Der Radius r des roten Kreises.
8 Sonderflle
á Fr r = 1 arbeiten wir mit dem Umkreis des regelm§igen n-Eckes.
á Fr r = 1, n = 2 und m = 4 ergibt sich die Situation des Satzes von Pythagoras. Die Darstellung ist etwas ungewohnt, indem ein Quadrat nach innen gerichtet ist und das Hypotenusenquadrat fehlt. Das Hypotenusenquadrat ergibt sich als Grenzfall, wenn P auf ein Streckenende zu liegen kommt.
á Fr r = 1, n = 3 und m = 3 ergibt sich die Situation der Abbildung 9. Die Flchensumme der blauen Dreiecke ist gleich dem Doppelten des Flcheninhaltes des Startdreiecks. Dies ergibt sich aus einem Grenzfall, wenn P auf eine Dreiecksecke zu liegen kommt.

Abb. 9: Dreiecke
á Fr r = 1, n = 4 und m = 4 ergibt sich die Situation der Abbildung 10. Die Flchensumme der blauen Quadrate entspricht dem Vierfachen des Flcheninhaltes des Startquadrates.
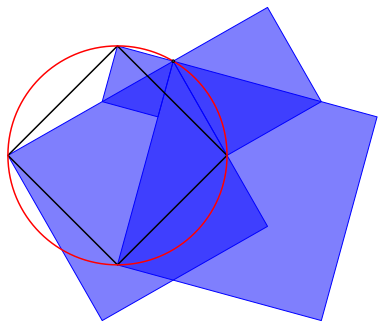
Abb. 10: Quadrate
á Fr r = 1, n = 20 und m = 20 ergibt sich etwas Lustiges (Abb. 11).

Abb. 11: 20-Ecke
Websites
Hans Walser: Kreisscharen
http://www.walser-h-m.ch/hans/Miniaturen/K/Kreisscharen2/Kreisscharen2.htm
Hans Walser: Flchensatz im Dreieck
www.walser-h-m.ch/hans/Miniaturen/F/Flaechensatz_im_Dreieck/Flaechensatz_im_Dreieck.htm