Hans Walser

 

 

Siebenbannstein

 

GDM Jahresversammlung 2015

Arbeitskreis Geometrie

Basel, 9. – 13. Februar 2015

 

Zusammenfassung

Ausgehend vom Siebenbannstein bei Lšrrach werden einige Gedanken zum regelmŠ§igen Siebeneck vorgestellt: Streifen- oder Knotenmodell, Faltmodell, Gelenkgeometrie, Winkeldrittelung, Modelle in der hyperbolischen Geometrie.

Historische und personelle LokalbezŸge zu Basel und Umgebung.

1        Der Siebenbannstein

Der Siebenbannstein (Abb. 1) befindet sich in der NŠhe von Lšrrach (nšrdlich von Basel) mitten im Wald (47¡ 36Õ 22.52Ò N / 07¡ 43Õ 05.12Ò E / 472 H). Hier trafen die alten Banne von Lšrrach, Stetten, Inzlingen, Hagenbach, Adelhausen, Ottwangen und Brombach zusammen.

 

    

Abb. 1: Der Siebenbannstein

 

Der Grenzstein hat einen siebeneckigen Querschnitt.

Das regelmŠ§ige Siebeneck lŠsst sich nicht mit Zirkel und Lineal konstruieren (Gau§), hingegen gibt es viele andere Methoden, ein regelmŠ§iges Siebeneck zu finden.

Viele der folgenden Methoden sind nicht exklusiv fŸr das Siebeneck. Es lassen sich entsprechend auch Vielecke mit anderen Eckenzahlen bilden.

2        Knotenmodelle aus Papierstreifen

2.1      FŸnfeck

Die Abbildung 2 illustriert die Konstruktion eines regelmŠ§igen FŸnfeckes als Knoten aus einem Papierstreifen.

 

    

Abb. 2: RegelmŠ§iges FŸnfeck

 

2.2      Siebeneck

Wenn wir beim Knoten eine Schlaufe mehr anbringen erhalten wir das regelmŠ§ige Siebeneck (Abb. 3). Der Verknotungsprozess braucht etwas FingerspitzengefŸhl, aber es geht.

 

Abb. 3: RegelmŠ§iges Siebeneck

 

Die Abbildung 4 zeigt die Topologie des Knotens. Es wurde ein Streifen mit unterschiedlicher FŠrbung auf den beiden Seiten verwendet.

 

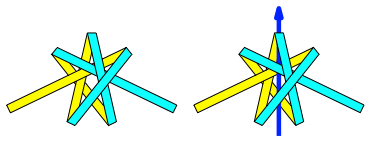
Abb. 4: Topologie des Knotens

 

Der Knoten hat eine senkrechte Drehsymmetrie-Achse. Die Drehsymmetrie ist kompatibel mit der FŠrbung.

Wenn wir allerdings den Streifen zum Siebeneck schlie§en sehen wir dass die FŠrbung mit zwei Farben nicht konsistent mšglich ist. Wir haben ein Mšbiusband (Abb. 5).

 

Abb. 5: Mšbiusband

 

Daher muss fŸr den Siebeneck-Knoten (wie auch schon fŸr den FŸnfeck-Knoten) ein beidseitig gleich gefŠrbter Streifen verwendet werden.

2.3      Neuneck

Jede zusŠtzliche Schlaufe im Knoten erhšht die Eckenzahl um zwei. Somit kšnnen alle regelmŠ§igen Vielecke mit ungerader Eckenzahl > 3 als Knoten hergestellt werden. Wir haben immer ein Mšbiusband. Die Abbildung 6 zeigt das regelmŠ§ige Neuneck.

 

Abb. 6: RegelmŠ§iges Neuneck

 

Der Autor gesteht, dass er hier mit einem durch Vorfalten prŠparierten Papierstreifen gearbeitet hat.

2.4      Gerade Eckenzahl

2.4.1    Vielfache von 4

FŸr ein regelmŠ§iges Vieleck mit 4, 8, 12, 16, ... Ecken kšnnen wir mit einem beidseitig unterschiedlich gefŠrbten Streifen arbeiten. Die Abbildung 7 zeigt exemplarisch die Situation fŸr ein Achteck.

 

    

Abb. 7: RegelmŠ§iges Achteck

 

2.4.2    Nombres impairement pairs

FŸr die ungeraden geraden Zahlen 6, 10, 14, 18, ... benštigen wir zwei ineinander verflochtene MšbiusbŠnder (Abb. 8 fŸr ein Sechseck).

 

    

Abb. 8: RegelmŠ§iges Sechseck

 

3        Scherengeometrie

Die Abbildung 9 zeigt eine symmetrische und eine asymmetrische Schere.

 

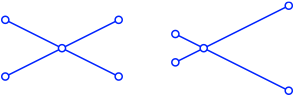
Abb. 9: Symmetrische und asymmetrische Schere

 

Zur Scherengeometrie vgl. (Walser, 2003).

3.1      Lineare Bewegung

Ein Set von symmetrischen Scheren fŸhrt zu einer linearen Bewegung (Abb. 10).

 

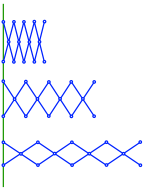
Abb. 10: Lineare Bewegung

 

Diese Technik wird bei HebebŸhnen verwendet (Abb. 11).

 

    

Abb. 11: HebebŸhne

 

3.2      GekrŸmmte Bewegung

Bei einem Set von asymmetrischen Scheren ergibt sich eine KrŸmmung. Bei Verwendung von sieben Scheren krŸmmen wir nun so lange, bis sich die Figur schlie§t. Die Spitzen des Siebensterns bilden ein regelmŠ§iges Siebeneck. Der Mittelpunkt des Siebenecks wird bei dieser Konstruktion nicht benštigt.

 

Abb. 12: KrŸmmung und Siebenstern

 

Dieses Vorgehen kann mechanisch mit Metallstreifen oder Kartonstreifen realisiert werden. Mit n Scheren ergibt sich ein regelmŠ§iges n-Eck.

Die Abbildung 13 mit Kartonstreifen illustriert, wie sich unterschiedliche Asymmetrie der Scheren auf den Stern auswirkt. Im Beispiel links unterteilt der mittlere Gelenkpunkt die Streifen im VerhŠltnis 2:1, im Beispiel rechts im VerhŠltnis 3:1.

 

    

Abb. 13: Unterschiedliche Asymmetrien

 

Dieses TeilverhŠltnis ŸbertrŠgt sich auf das RadienverhŠltnis von Um- und Inkreis (Abb. 14).

 

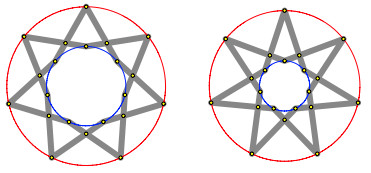
Abb. 14: Um- und Inkreise

 

3.3      Dreiecke

Im Beispiel der Abbildung 15 wir ebenfalls das Prinzip der Scherengeometrie.

 

    

Abb. 15: Kongruente gleichseitige Dreiecke

 

4        FŠchergeometrie

In der FŠchergeometrie gehen wir vom Mittelpunkt aus.

4.1      Siebenteiliger FŠcher

Wir šffnen den siebenteiligen FŠcher und schlie§en die Enden zusammen (Abb. 16).

 

Abb. 16: FŠcher

 

4.2      Winkeldrittelung

Der Stern der Abbildung 17 ist aus baugleichen Teilen wie die Figur der Abbildung 16 gebaut. Mit einer Modifikation erhalten wir aus nur drei Scheren ein WinkeldrittelungsgerŠt.

 

    

Abb. 17: Winkeldrittelung

 

5        Schirmgeometrie

Im Unterschied zur FŠchergeometrie benštigen wir fŸr die Schirmgeometrie den Raum.

5.1      Schirme

Viele Schirme sind achtteilig (Abb. 18). Binden wir vor dem …ffnen zwei Speichen zusammen, ergibt sich ein regelmŠ§iges Siebeneck.

 

    

Abb. 18: Schirmgeometrie

 

5.2      Faltgeometrie

In der Figur der Abbildung 19 wird ein durch Falten eines Papiers hergestelltes ebenes Achteck nach dem Identifizieren zweier Sechzehntel (durch die BŸroklammer) zu einer rŠumlichen siebenteiligen Pyramide.

 

    

Abb. 19: Siebeneck durch Falten und †berlappen

 

5.3      PapierblŸte

Die Abbildung 20 zeigt eine aus Papierschiffchen hergestellte siebenteilige PapierblŸte in geschlossenem und gešffnetem Zustand. Beim …ffnen Šndert sich das Profil (der Meridian). Wir haben also die gleiche Situation wie beim …ffnen des Schirmes.

 

    

Abb. 20: PapierblŸte

 

6        Plastikband

Zu Modellen aus Plastikband vgl. (Walser, 2010).

6.1      Vom Sechseck zum FŸnfeck

Die Abbildung 21 zeigt zunŠchst ein aus PlastikbŠndern (Verpackungsmaterial) hergestelltes Geflecht aus regelmŠ§igen Sechsecken und Dreiecken. Werden die Sechsecke zu FŸnfecken reduziert, krŸmmt sich die Sache in den Raum und wir erhalten eine Halbkugel. — SpŠter werden wir Ÿberlegen, was geschieht, wenn wir die Sechsecke zu Siebenecken erweitern.

 

    

Abb. 21: Vom Sechseck zum FŸnfeck

 

6.2      Vom FŸnfeck zum Viereck

In der Abbildung 22 ist zunŠchst die Halbkugel der Abbildung 21 zur Kugel ergŠnzt. Nun reduzieren wir die FŸnfecke zu Vierecken. Dadurch verkleinert sich die Kugel.

 

    

Abb. 22: Vom FŸnfeck zum Viereck

 

6.3      Dichteste Kugelpackung

Die kleine Kugel der Abbildung 22 kšnnen wir fŸr eine dichteste Kugelpackung (Kepler, Hales) verwenden (Abb. 23). Die Positionen der MustertŸtenklammern sind nŠmlich genau die Kontaktpunkte zu den Nachbarkugeln. Damit kšnnen zwei sich berŸhrende Kugeln mit einer durchgehenden MustertŸtenklammer verbunden werden.

 

    

Abb. 23: Kugelpyramiden

 

6.4      Glucker oder Glugger

Die dichteste Kugelpackung kann auch mit einer Pyramide aus Glaskugeln illustriert werden. Solche Glaskugeln (Murmeln) hei§en auf Baseldeutsch Glucker oder Glugger. Es gibt in Basel am Heuberg 34 ein Haus namens Gluggerturm mit einer aufschlussreichen Inschrift (Abb. 24).

 

Abb. 24: Eine umwŠlzende Erfindung

 

6.5      Vom Viereck zum Dreieck

Wir reduzieren die Vierecke zu Dreiecken und erhalten Kugeln mit acht Dreiecken (Abb. 25). Diese kšnnen ebenfalls zu einem Cluster zusammengeheftet werden. Es handelt sich um die WŸrfelpackung.

 

    

Abb. 25: Dreiecke und WŸrfelpackung

 

6.6      Vom Sechseck zum Siebeneck

Wir erweitern nun die Sechsecke zu Siebenecken (Abb. 26). Dadurch krŸmmt sich das Modell ebenfalls in den Raum, aber in verschiedenen Richtungen. Wir kommen zur hyperbolischen Geometrie.

 

    

Abb. 26: Hyperbolische Geometrie

 

Die Abbildung 27 zeigt den fŸr das hyperbolische Modell der Abbildung 26 relevanten Ausschnitt aus dem Kreismodell von PoincarŽ.

 

Abb. 27: Ausschnitt aus dem Modell von PoincarŽ

 

6.7      Johann Heinrich Lambert

Johann Heinrich Lambert (1728-1777) wurde in MŸhlhausen (heute Mulhouse) geboren.

 

                       

Abb. 28: Johann Heinrich Lambert (1728-1777)

 

Das elsŠssische MŸhlhausen ist eine Nachbarstadt von Basel und gehšrte damals zur Schweiz. Lambert arbeitete zeitweise bei der Basler Zeitung. Bekannt wurde er durch seinen Beweis der IrrationalitŠt von ¹. Lambert war einer der Pioniere der hyperbolischen Geometrie. Er schlug vor, die hyperbolische Geometrie als die Geometrie auf einer Kugel mit dem Radius i zu verstehen.

6.8      RotationsflŠchen

Die Abbildung 29 zeigt im Prinzip zweimal die gleiche Figur mit Siebenecken. ZusŠtzlich sind Diagonalen der Siebenecke eingebaut, links die kurzen, rechts die langen Diagonalen.

 

    

Abb. 29: RotationsflŠchen

 

Literatur

Walser, Hans (2003): Gleitfiguren und Gelenkfiguren. Mathematikinformation, Nr. 38, 15. Januar 2003, S. 17-34

Walser, Hans (2010): Handgreifliche Modelle der Kugelgeometrie und der hyperbolischen Geometrie. MU Der Mathematikunterricht. Elemente nichteuklidischer Geometrien. Jahrgang 56. Heft 6. Dezember 2010. Friedrich Verlag, Seelze. S. 28-37.

 

Last modified: 7. Oktober 2014