Der Raum und das DIN-Format

Hans Walser

12. Januar 2015

Toeplitz-Kolloquium, Bonn

Zusammenfassung: Ausgehend von didaktischen und erkenntnistheoretischen Problemen der Raumgeometrie werden zunächst einige Modelle von Polyedern vorgestellt, welche aus Papier oder Karton im DIN-Format hergestellt werden können. Anschließend wird die Grundidee des DIN-Formates auf andere Figuren übertragen, wobei wiederum der Raum eine wichtige Rolle spielt.

1 Was sehen wir?

Zum Verständnis der didaktischen Schwierigkeiten in der Raumgeometrie ist es naheliegend sich zunächst das zweidimensionale Analogon vor Augen zu halten.

1.1 Die so genannte ebene Geometrie

Die Geometrie in der Ebene ist nicht zweidimensional. Sie ist in den dreidimensionalen Raum eingebettet. Wir Menschen – Schüler wie Lehrer – sehen aus der dritten Dimension auf die zweidimensionale Geometrie-Ebene hinunter. Die ebene Geometrie wird sozusagen aus der Feldherrenperspektive präsentiert. Ganz anders sah es der Landsknecht im Dreck oder der Fahrer eines Jagdpanzers durch seinen Sehschlitz.

1.2 Raumgeometrie

In der Raumgeometrie ist die Situation grundsätzlich anders. Wir leben selber im Raum. Wir stecken sozusagen mit dem Kopf in der Suppe, die wir auslöffeln sollten. Um eine dreidimensionale Geometrie von derselben Qualität wie die zweidimensionale Geometrie zu erhalten, müssten wir aus der vierten Dimension auf den dreidimensionalen Raum hinunterschauen können.

1.3 Zweidimensionale Geometrie für Bildschirmbewohner

Unsere Probleme mit der dreidimensionalen Geometrie lassen sich illustrieren, indem wir uns die Situation von Leuten versetzen, welche in einer zweidimensionalen Welt leben. Also Leute aus Flatland (Abbott 1884, Burger 1978), Flachländer oder Screenbewohner.

Die Schulwandtafel der Flachländer ist eindimensional, die Flachlandlehrerin hat darauf eine recht bekannte Figur gezeichnet (Abb. 1a).

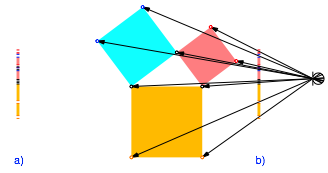
Abb. 1: Eine recht bekannte Figur

Wir erkennen die Figur erst in der Sicht aus der dritten Dimension (Abb. 1b). Ich frage mich, ob die Flachländer den Satz des Pythagoras je erkannt haben, und wenn ja, wie sie ihn beweisen konnten.

Vielleicht würden wir aus der 4d-Sicht auf die 3d-Raumgeometrie eine viel reichhaltigere Geometrie als die uns bekannte Raumgeometrie sehen. Das ist aber reine Spekulation und ähnlich irrelevant wie die Frage ob es ein Leben nach dem Tod gibt oder ob das Licht im Kühlschrank wirklich ausgeht wenn wir die Tür schließen.

2 Puzzles

Die Abbildung 2 zeigt ein scheinbar zweidimensionales Puzzle.

Abb. 2: Puzzle

Um das noch fehlende Puzzle-Teil rechts oben einzufügen, müssen wir es allerdings in die dritte Dimension anheben, in der Luft verschieben und etwas drehen und dann einsenken. Diese Operation ist für Flachländer nicht machbar. Sie können zwar durch Ausmessen feststellen, dass das Puzzleteil hineinpasst (statisch), aber sie können es nicht einpassen (dynamisch). Ein 2d-Puzzle funktioniert nur im 3d-Raum.

Die Abbildung 3 zeigt ein entsprechendes Beispiel im 3d-Raum (vgl. [1], S. 13 und (Maier, 1998, S. 25)).

Abb. 3: „Unmögliches“ 3d-Puzzle

Die fehlende Ecke passt zwar hinein, lässt sich aber nicht einpassen. Auf jeder Seitenfläche des Würfels bräuchten wir eine Ausweichrichtung senkrecht zur jeweiligen Seitenfläche. Dies ist simultan nur in der vierten Dimension möglich.

3 Fazit

„Unsere“ 3d-Geometrie ist ein Abklatsch der 2d-Geometrie.

4 Das DIN-Format

Wenn wir ein DIN A4 Papier längs der kurzen Mittellinie falten, ergibt sich ein doppellagiges DIN A5 Papier (Abb. 4). Dieses hat nun dieselbe Form (Ähnlichkeit), also dieselben Seitenverhältnisse wie das DIN A4 Papier. Dies kann durch Anlegen an eine gemeinsame Diagonale nachgeprüft werden.

Abb. 4: DIN A4 und DIN A5

Mit der Schmalseite 1 und der Langseite x für das DIN A4 Rechteck erhalten wir aus der Ähnlichkeit:

Dieses Seitenverhältnis kann durch Falten nachgeprüft werden (Abb. 5). Dabei benützen wir den Sachverhalt, dass im Quadrat die Diagonalen-Länge das der Seitenlänge ist.

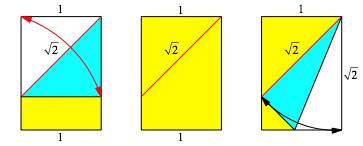
Abb. 5: Kontrolle durch Falten

5 Das DIN-Rechteck in Würfel und Tetraeder

Zwei diametrale Würfelkanten spannen ein Rechteck im DIN-Format auf. Daher können mit Papieren oder Karten im DIN-Format Würfelmodelle gebaut werden.

5.1 Diagonalflächen

Die Abbildung 6 zeigt ein Modell aus sechs A6-Karten. Schnittmuster und Bauanleitung siehe (Walser, 2009) und (Walser, 2013, S. 45f).

Abb. 6: Würfelmodell aus sechs A6 Karten

5.2 Kantenmodell des Würfels

Als Baumaterial dient Papier im DIN A6-Format. Geeignet ist dazu Papier der Stärke 80 g/m², das vom Format A4 auf A6 zugeschnitten wird.

Für jede Kante braucht es ein Papier.

Für den Faltprozess verwenden wir eine etwas festere A6-Karte als Faltlehre. Wir legen diese Faltlehre diagonal auf ein A6-Papier und falten die vorstehenden Ecken des darunterliegenden Papiers nach vorne über die Faltlehre (Abb. 7a, 7b). Dann entfernen wir die Faltlehre. Der Umriss des Papiers ist nun ein Rhombus (Abb. 7c).

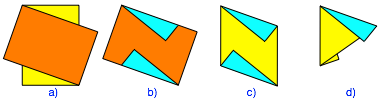
Abb. 7: Faltvorgang

Nun falten wir die untere Spitze des Rhombus nach hinten unter die obere Spitze (Abb. 7d). Diese letzte Faltlinie wird zu einer Kante des Würfels. Was an dieser Kante noch vorsteht, kann zurückgebogen oder abgeschnitten werden. Damit haben wir unser Bauteil. Es hat die Form eines doppellagigen gleichschenkligen Dreiecks mit zwei Verbindungslaschen zum Einschieben in die Nachbarteile.

Die Abbildung 8 zeigt ein geöffnetes Bauteil von innen. Die Spitzen der beiden Rhomben-Hälften müssen vor dem Zusammenbau des Modells noch aufeinander gelegt werden. Diese Spitzen kommen alle in den Mittelpunkt des Würfels zu liegen. Die Seiten der Rhomben werden zu halben Raumdiagonalen des Würfels.

Wir benötigen 12 Bauteile. Beginnend mit drei verschieden farbigen A4-Papieren, die wir zu A6-Papieren vierteln, erhalten wir drei Sätze von je vier gleichfarbigen Bauteilen. Damit können wir den jeweils vier parallelen Würfelkanten dieselbe Farbe zuordnen (Abb. 9).

Abb. 8: Bauteil

Und nun kommt das Interessante, der Zusammenbau (Abb. 9). Wir schieben jeweils eine Verbindungslasche zwischen die beiden gleichschenkligen Dreiecke des Nachbarbauteils. Dabei achten wir darauf, dass an jeder halben Raumdiagonale des Würfels drei Bauteile in den drei verschiedenen Farben zusammen kommen. Parallele Würfelkanten haben dieselbe Farbe.

Abb. 9: Kantenmodell des Würfels

Es empfiehlt sich, den Zusammenbau schrittweise mit Büroklammern zu fixieren. An jeder Ecke des Würfels ergeben sich schließlich drei Büroklammern.

Wenn alles sitzt, können die Büroklammern schrittweise entfernt und durch eine Heftklammer mit dem Tacker ersetzt werden. Dabei hat man den Ehrgeiz die Klammern symmetrisch einzubringen.

Für das Modell der Abbildung 9 wurden drei Farben verwendet und die Bauteile so angeordnet, dass parallele Kanten dieselbe Farbe haben. Wir können aber auch mit vier Farben arbeiten und die zugehörigen Kanten paarweise windschief einbauen. Dann sehen wir in jeder Seitenfläche des Würfels in eine Pyramide mit jeweils einer anderen zyklischen Anordnung der vier Farben. Im Würfelmodell kommen genau diese sechs zyklischen Anordnungen vor.

5.3 Kantenmodell des Tetraeders

Analog zum Kantenmodell des Würfels kann ein Kantenmodell des Tetraeders gebaut werden (Abb. 10). Dazu müssen wir im Faltvorgang der Abbildung 7d längs der langen Rhombendiagonalen falten. Wir benötigen sechs Bauteile.

Abb. 10: Kantenmodell des Tetraeders

6 Ausschöpfen des A0-Rechteckes

Das DIN-Format ist flächenmäßig ans metrische System angebunden. Das DIN A0 Papier hat einen Flächeninhalt von einem Quadratmeter.

6.1 Die klassische Art

Wir können mit einem Set von DIN-Rechtecken A1, A2, A3, ... ein A0-Rechteck ausschöpfen (Abb. 11).

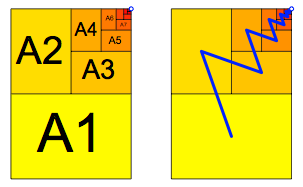
Abb. 11: Ausschöpfung des A0-Rechteckes

Wenn wir die Mitten aufeinanderfolgender Rechtecke verbinden, ergibt sich eine Zickzack-Linie, welche in den Grenzpunkt rechts oben mündet.

6.2 Spiralförmige Anordnung

Wir können das Set von Rechtecken A1, A2, A3, ... aber auch spiralförmig gemäß Abbildung 12a anordnen.

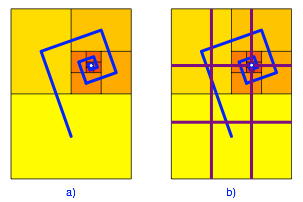
Abb. 12: Spiralförmige Anordnung. Drittel und Neuntel

Der Grenzpunkt ist ein „Drittelpunkt“ (Abb. 12b). Dies kann wie folgt eingesehen werden: Wenn wir auf der Höhe des Grenzpunktes von rechts her einfahren, treffen wir nur Hochformat-Rechtecke, und zwar der Reihe nach A4, A8, A12, ... . Diese haben im Vergleich zum Startrechteck die Breiten , , , ... . Für den Abstand vom rechten Rand erhalten wir somit die geometrische Reihe:

6.3 DIN-Code

Ein violettes Rechteck der Abbildung 12b hat das Seitenverhältnis des DIN-Formates. Es bedeckt einen Neuntel des A0-Rechteks. Welchen DIN-Code hat es?

Dazu vergleichen wir mit den Flächenanteilen im DIN-System.

Wir sehen, dass unser violettes Rechteck zwischen A3 und A4 liegt, gefühlsmäßig näher an A3. Rechnerisch erhalten wir:

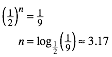
6.4 Andere Grenzpunkte

Jeder Punkt im Innern oder auf dem Rand des A0-Rechteckes kann Grenzpunkt werden. Dazu verwenden wir folgenden Algorithmus („Die Katze schleicht um den heißen Brei“): Wir füllen das A0-Rechteck mit einem Set von DIN-Rechtecken A1, A2, A3, ... so auf, dass der anvisierte Grenzpunkt nie ins Innere eines Set-Rechteckes gelangt. Die Abbildung 13 zeigt die ersten fünf Schritte und die Grenzfigur.

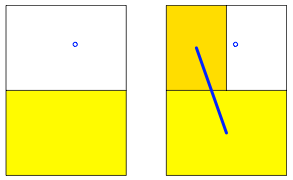
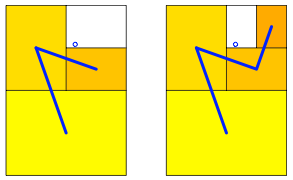
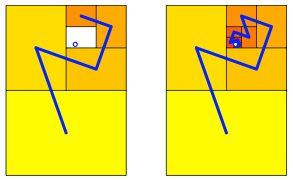
Abb. 13: Beliebiger Grenzpunkt

Natürlich wird der Algorithmus ambivalent, wenn der anvisierte Grenzpunkt auf den Rand eines Set-Rechteckes zu liegen kommt. Dies ist genau dann der Fall, wenn die x-Koordinate und/oder die y-Koordinate modulo eine abbrechende Dualbruchentwicklung haben.

In diesem Fall entscheiden wir uns für „unten“ beziehungsweise „links“. Dieser Entscheid ist von derselben Qualität wie der Entscheid, ein Halbes im Dezimalsystem durch 0.5 und nicht durch 0.4999... darzustellen.

Die Abbildung 14 zeigt die Situation mit dem Grenzpunkt in der Mitte des A0-Rechtecks.

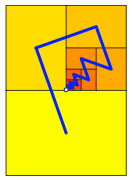
Abb.14: Grenzpunkt in der Mitte

Die Figur ist asymmetrisch, muss es sein, da bei einer Symmetrie im A0-Rechteck jedes Teil doppelt oder vierfach erscheinen müsste.

6.5 Mächtigkeiten

Ein Set von DIN-Rechtecken A1, A2, A3, ... ist abzählbar (es ist ja bereits nummeriert). Es hat die Mächtigkeit . Da jeder Punkt eines Din A0-Rechteckes Grenzpunkt sein kann, haben wir für diese Punkte nach unserem Algorithmus die Mächtigkeit , da es für jedes Set-Rechteck zwei Positionsmöglichkeiten gibt.

6.6 Historisches

Abb. 15: Wilhelm Ostwald (1853-1932). Walter Porstmann (1886-1959)

6.6.1 Wilhelm Ostwald

Der Nobelpreisträger Wilhelm Ostwald (1853-1932, Nobelpreis für Chemie 1909, Abb. 15a) entwickelte 1911 ein System von Papierformaten, das er als Weltformat bezeichnete (Ostwald 1911). Geometrische Grundlage ist das Rechteck mit dem Seitenverhältnis , also wie beim heutigen DIN-Rechteck. Das System wurde längenmäßig auf das metrische System bezogen, indem das kleinste Rechteck (Weltformat I) die kurze Seite 1cm aufwies.

6.6.2 Walter Porstmann

Der Ingenieur, Mathematiker und Normungstheoretiker Walter Porstmann (1886-1959, Abb. 15b) war zeitweise Assistent von Wilhelm Ostwald. Er engagierte sich für ein System, das nicht längenmäßig, sondern flächenmäßig mit dem metrischen System verbunden ist, also . So entstand das heute noch verwendete DIN-System.

7 Die DIN-Idee. Andere Figuren

Gibt es andere Figuren, die in zwei kongruente, zur Ausgangsfigur ähnliche Teilfiguren zerlegbar sind?

Die Frage ist allgemein gehalten, es ist nicht von Halbieren die Rede, sondern nur von Zerlegen.

7.1 DIN-Parallelogramm

Wir können die DIN-Rechtecke zu Parallelogrammen verscheren (Abb. 16).

Abb. 16: Parallelogramme

Die Teilparallelogramme sind ungleichsinnig ähnlich zum Startparallelogramm.

7.2 Das rechtwinklig-gleichschenklige Dreieck

Das naheliegende Beispiel ist das rechtwinklig-gleichschenklige Dreieck (Abb. 17). Bei der einfachsten Zerlegung gibt es einen Grenzpunkt unten rechts.

Abb. 17: Das rechtwinklig-gleichschenklige Dreieck

Es gibt im rechtwinklig-gleichschenkligen Dreieck ebenfalls eine spiralförmige Anordnung (Abb. 18). Der Grenzpunkt führt zu Fünfteln.

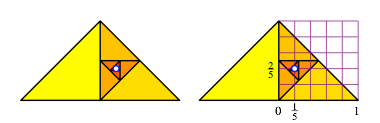
Abb. 18: Spiralförmige Anordnung

Die Figur kann auch aus einem halben Origami Papier durch fortlaufendes Falten erreicht werden (Abb. 19 und Abb. 20). Für das Falten ist ein dreidimensionaler Raum erforderlich.

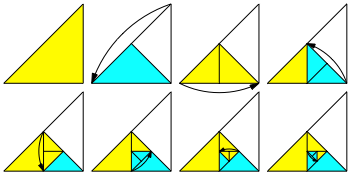
Abb. 19: Faltprozess

Abb. 20: Faltmodell

Die Thaleskreise der Teildreiecke verlaufen durch den Grenzpunkt, ebenso eine Auswahl von Seitenhalbierenden (Abb. 21).

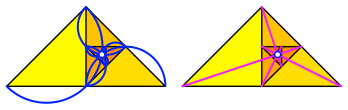
Abb. 21: Thaleskreise. Seitenhalbierende

8 Der Sprung in den Raum

8.1 DIN-Quader

Wird ein Quader mit dem Kantenverhältnis halbiert, ergeben sich zwei Quader mit dem Kantenverhältnis . Diese sind ähnlich zum ursprünglichen Quader.

Die Abbildung 22 zeigt eine Anordnung eines DIN-Quader-Sets analog zur klassischen Anordnung eines Sets von DIN-Rechtecken.

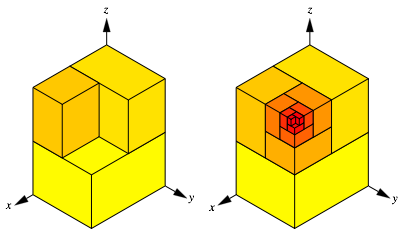
Abb. 22: Anordnung

Während bei Rechtecken nur zwischen Querformat und Hochformat unterschieden werden kann, brauchen wir hier drei Anaordnungsformate. Dazu dient das beigefügte Koordinatensystem. Der erste Quader hat seine längsten Kanten in der x-Richtung, der zweite Quader hat seine längsten Kante in der y-Richtung und der dritte Quader in der z-Richtung. Der vierte Quader hat seine längsten Kanten wiederum in der x-Richtung.

Als Stimmungsbild (Abb. 23) reale DIN-Quader.

Abb. 23: DIN-Kisten

8.2 Spiralen

8.2.1 Schnecke

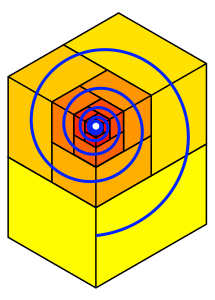
Die Quader der Abbildungen 22 und 23 sind in einer räumlichen Spirale wie bei einer Wasserschnecke angeordnet. Der Grenzpunkt ist das Zentrum der Spirale (Abb. 24).

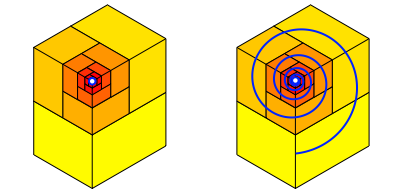
Abb. 24: Räumliche Spirale

8.2.2 Grenzpunkt im Innern

Gibt es analog zur Abbildung 12 eine Spirale mit dem Grenzpunkt im Innern?

Das Problem ist – einmal mehr – unsere Beschränkung auf drei Dimensionen. Wir können nicht aus der vierten Dimension ins Innere der Kisten blicken. Daher überlegen wir zunächst, wie eine Flachländerin die zweidimensionale spiralförmige Anordnung der Abbildung 12 baut. Ihr Problem ist, dass sie nach Hinlegen der ersten vier Rechtecke entweder ausgeschlossen oder eingeschlossen ist.

Ideal wäre, wenn sie im Zentrum beginnen und dann die Spirale darum herum wickeln könnte. Das geht aber nicht, da das Zentrum im Unendlichen ist.

Sie beginnt daher außen mit den beiden ersten Rechtecken (Abb. 25). Dann legt sie das dritte und vierte Rechteck separat hin. Das fünfte und sechste Rechteck wird an die beiden ersten angefügt, das siebte und achte an das dritte und vierte und so weiter.

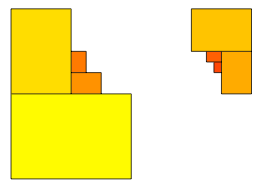
Abb. 25: Vorgehen der Flachländerin

Schließlich werden die beiden Teilfiguren zusammengeschoben.

Die kleine Teilfigur ergibt sich aus der großen durch eine zentrische Streckung mit dem Faktor .

Analog können wir mit unseren Kisten vorgehen.

Zunächst legen wir die ersten drei Kisten hin gemäß Abbildung 26.

Die nächsten drei Kisten legen wir separat hin, aber im Vergleich zu den ersten drei Kisten in spiegelbildlicher Anordnung. Dann weiter wie in der Ebene. Die kleine Teilfigur müssen wir vor dem Einschieben noch auf den Kopf stellen.

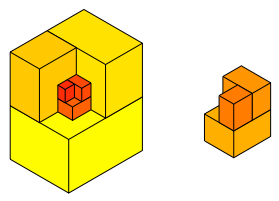
Abb. 26: Vorgehen im dreidimensionalen Raum

Der Grenzpunkt ist wiederum ein „Drittelpunkt“.

8.2.3 Orientierungsumkehrung

Die spiegelbildliche Anordnung der beiden Teifiguren ist deshalb erforderlich, weil im Raum die zentrische Streckung mit dem Faktor eine orientierungsumkehrende Abbildung ist. Man kann das mit den realen Kisten der Abbildung 23 ausprobieren. Allgemein ist im Raum (im Unterschied zur Ebene) eine zentrische Streckung mit negativem Faktor orientierungsumkehrend. Man kann sich das am Sonderfall der Punktspiegelung (Faktor –1) leicht klarmachen: wir halten eine Kugel so mit beiden Händen, dass entsprechende Finger (Daumen-Daumen etc.) diametral liegen (Abb. 27).

Abb. 27: Punktspiegelung im Raum

Die Punktspiegelung am Kugelmittelpunkt bildet die rechte Hand auf die linke Hand ab.

Es ist daher etwas fragwürdig, die Punktspiegelung im Raum als Analogon der Punktspiegelung in der Ebene zu bezeichnen.

8.2.4 Eckige Spirale

Wir verbinden nun die Mittelpunkte aufeinanderfolgender Quader zu einer Zickzacklinie. Die Abbildung 28a zeigt dies in einer Phantomdarstellung, die Abbildung 28b in klassischer Manier mit Grund-, Auf- und Kreuzriss.

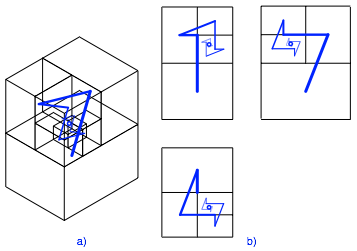
Abb. 28: Zickzackzocklinie

Eigentlich ist es eine Zickzackzocklinie.

8.3 DIN-Hyperquader

Im vierdimensionalen Raum ergeben sich durch

oder in anderer Schreibweise

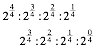
die Kanten zweier aufeinanderfolgender 4d-DIN-Hyperquader. George Pólya (1887-1985, Abb. 29) hätte in dieser Situation allerdings von einer Verallgemeinerung durch Verwässerung gesprochen.

Abb. 29: George Pólya

8.4 Gleichtemperierte 12-Ton-Stimmung

Wir verwässern weiter zum 12d-DIN-Hyperquader.

Das haben wir zwar noch nie gesehen, aber schon gehört. Es sind die Frequenzverhältnisse der Gleichtemperierte 12-Ton-Stimmung.

8.5 Die Jakobsleiter

Und ihm träumte; und siehe, eine Leiter stand auf der Erde,

die rührte mit der Spitze an den Himmel, und siehe,

die Engel Gottes stiegen daran auf und nieder.

Gen 28, 11

Die Abbildung 30a zeigt die ersten Sprossen der Jakobsleiter.

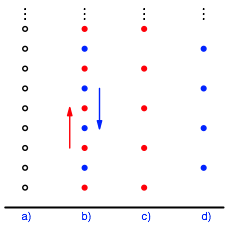
Abb. 30: Jakobsleiter

Auf der einen Seite der Leiter steigen die Engel hinauf, auf der anderen Seite hinunter. Damit sie sich nicht gegenseitig auf den Füßen herumtreten, haben sie festgelegt, dass die aufsteigenden Engel nur die Sprossen mit ungeraden Nummern verwenden, die absteigenden nur die Sprossen mit geraden Nummern (Abb. 30b). Damit zerfällt die Jakobsleiter in zwei Teil-Jakobsleitern, die zur ursprünglichen Jakobsleiter ähnlich sind (Abb. 30c und 30d). Wir haben also das Prinzip des DIN-Formates.

Der Reduktionsfaktor ist 2. Das Wort Reduktionsfaktor ist syntaktisch richtig, semantisch falsch, da Sprossenhöhne nicht reduziert, sondern verdoppelt wird. Unter dem Aspekt eines Fraktals ergibt sich die Mandelbrot-Dimension D (fraktale Dimension):

Literatur

Abbott, Edwin A. (1884): Flatland. A Romance of Many Dimensions. London: Seeley.

Burger, Dyonis (1978): Silvestergespräche eines Sechsecks. Köln: Aulis. ISBN 3-7614-0085-3.

Maier, Peter Herbert (1998): Räumliches Vorstellungsvermögen – Unterschiede zwischen Mann und Frau? In Informationsblätter für Darstellende Geometrie (IBDG) 1/1998. S. 23-31.

Ostwald, Wilhelm (1911): Die Weltformate für Drucksachen. Ansbach: Seybold’s Buchhandlung.

Walser, Hans (2009): Steckmodelle. MU Der Mathematikunterricht. Polyeder im Mathematikunterricht. Jahrgang 55. Heft 1. Februar 2009. Friedrich Verlag, Seelze. S. 38-47.

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.

Internetseiten

[1] http://www.geotic.at/docs/GEODIKON-GDM-Saarbruecken-140912-de.pdf (abgerufen 21. 9. 2014)

Adresse des Autors:

Hans Walser

Gerlikonerstr. 29

CH-8500 Frauenfeld

hwalseratbluewin.ch

www.walser-h-m.ch/hans/