Hans Walser

Das DIN-Format

PH Bern

Mittwoch, 13. Juni 2018

Zusammenfassung

Das DIN-Format ist mehr als ein Stück Papier und die Quadratwurzel aus Zwei.

Wir treffen auf Spiralen, Grenzpunkte, Fragen der Abzählbarkeit, das Delische Problem, die gleichtemperierte 12-Ton-Stimmung, Jakobs Himmelsleiter, das Silberne Rechteck, Faltprobleme und Legespiele nach Fröbel.

Weiter lernen wir ebene und räumliche Faltmodelle kennen, die nur mit Papier im DIN-Format möglich sind. Insbesondere bauen wir Kantenmodelle des Würfels und des Tetraeders und falten ein regelmäßiges Achteck.

Material und Werkzeuge:

· Papier (75 – 90 g/m²), Formate A4 und A6, verschiedene Farben

· Bostitch (Klammermaschine) und Reserveklammern

1 Wurzel aus zwei

Wenn wir ein DIN A4 Papier längs der kurzen Mittellinie falten, ergibt sich ein doppellagiges DIN A5 Papier. Dieses hat nun dieselbe Form (Ähnlichkeit), also dieselben Seitenverhältnisse wie das DIN A4 Papier, wie durch Anlegen an eine gemeinsame Diagonale nachgeprüft werden kann.

DIN A4 und DIN A5

Mit der Schmalseite 1 und der Langseite x für das DIN A4 Rechteck erhalten wir aus der Ähnlichkeit:

Dieses Seitenverhältnis kann durch Falten nachgeprüft werden. Dabei benützen wir den Sachverhalt, dass im Quadrat die Diagonalen-Länge das der Seitenlänge ist.

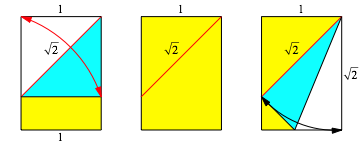
Kontrolle durch Falten

Beim Abschneiden eines Quadrates vom DIN-Rechteck (etwa beim Zuschneiden von Origami-Papier) bleibt unten ein Rechteck mit dem Seitenverhältnis übrig. Dies ist das so genannte Silberne Rechteck. Es hat ähnliche Eigenschaften wie das Goldene Rechteck (Walser 2013b).

2 Ausschöpfen des A0-Rechteckes

2.1 Die klassische Art

Wir können mit einem Set von DIN-Rechtecken A1, A2, A3, ... ein A0-Rechteck ausschöpfen. Die Rechtecke sind im Wechsel im Quer- und Hochformat.

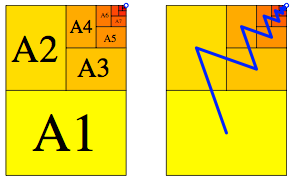
Ausschöpfung des A0-Rechteckes

Wenn wir die Mitten aufeinanderfolgender Rechtecke verbinden, ergibt sich eine Zickzack-Linie, welche in den Grenzpunkt rechts oben mündet.

2.2 Spiralförmige Anordnung

Wir können das Set von Rechtecken A1, A2, A3, ... aber auch spiralförmig anordnen.

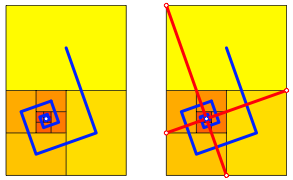
Spiralförmige Anordnung

Der Grenzpunkt ergibt sich durch Einzeichnen geeigneter Halbdiagonalen.

Der Grenzpunkt hat „Drittelkoordinaten“.

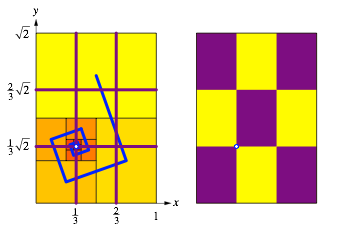
Drittel bei den Koordinaten

Das kann wie folgt eingesehen werden: Wenn auf der Höhe des Grenzpunktes von links her einfahren, treffen wir nur Hochformat-Rechtecke, und zwar der Reihe nach A4, A8, A12, A16, ... . Diese haben im angegebenen Koordinatensystem die Breiten , , , , ... . Für die x-Koordinate des Grenzpunktes ergibt sich daher die geometrische Reihe:

Ein violettes Rechteck der vorstehenden Abbildung hat das Seitenverhältnis des DIN-Formates. Es bedeckt einen Neuntel des A0-Rechteks. Welchen DIN-Code hat es?

Dazu vergleichen wir mit den Flächenanteilen im DIN-System.

Wir sehen, dass unser violettes Rechteck zwischen A3 und A4 liegt, gefühlsmäßig näher an A3. Rechnerisch erhalten wir:

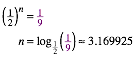
2.3 Andere Grenzpunkte

Jeder Punkt im Innern oder auf dem Rand des A0-Rechteckes kann Grenzpunkt werden. Dazu verwenden wir folgenden Algorithmus („Die Katze schleicht um den heißen Brei“): Wir füllen das A0-Rechteck mit einem Set von DIN-Rechtecken A1, A2, A3, ... so auf, dass der anvisierte Grenzpunkt nie ins Innere eines Set-Rechteckes gelangt. Die folgende Abbildung zeigt die ersten fünf Schritte und die Grenzfigur.

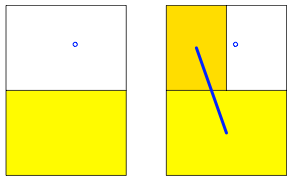
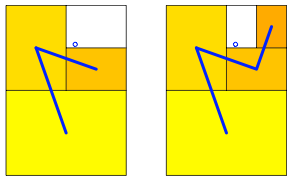
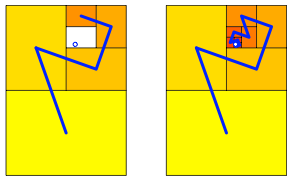
Beliebiger Grenzpunkt

Natürlich wird der Algorithmus ambivalent, wenn der anvisierte Grenzpunkt auf den Rand eines Set-Rechteckes zu liegen kommt. Dies ist genau dann der Fall, wenn die x-Koordinate und/oder die y-Koordinate modulo eine abbrechende Dualbruchentwicklung haben.

In diesem Fall entscheiden wir uns für „unten“ beziehungsweise „links“. Dieser Entscheid ist von derselben Qualität wie der Entscheid, ein Halbes im Dezimalsystem durch 0.5 und nicht durch 0.4999... darzustellen.

Die folgende Abbildung zeigt die Situation mit dem Grenzpunkt in der Mitte des A0-Rechtecks.

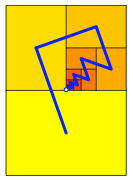
Grenzpunkt in der Mitte

Die Figur ist asymmetrisch, muss es sein, da bei einer Symmetrie im A0-Rechteck jedes Teil doppelt oder vierfach erscheinen müsste.

2.4 Mächtigkeiten

Ein Set von DIN-Rechtecken A1, A2, A3, ... ist abzählbar (es ist ja bereits nummeriert). Es hat die Mächtigkeit . Da jeder Punkt eines Din A0-Rechteckes Grenzpunkt sein kann, haben wir für diese Punkte nach unserem Algorithmus die Mächtigkeit , da es für jedes Set-Rechteck zwei Positionsmöglichkeiten gibt.

3 Andere Figuren

Gibt es andere Figuren, die in zwei kongruente, zur Ausgangsfigur ähnliche Teilfiguren zerlegbar sind?

Die Frage ist allgemein gehalten, es ist nicht von Halbieren die Rede, sondern nur von Zerlegen.

3.1 Strecke

Das einfachste Beispiel ist eine Strecke.

Strecke

3.2 DIN-Parallelogramm

Wir können die DIN-Rechtecke zu Parallelogrammen verscheren.

Parallelogramme

Die Teilparallelogramme sind ungleichsinnig ähnlich zum Startparallelogramm.

3.3 Das rechtwinklig-gleichschenklige Dreieck

Das naheliegende Beispiel ist das rechtwinklig-gleichschenklige Dreieck. Bei der einfachsten Zerlegung gibt es einen Grenzpunkt unten rechts.

Das rechtwinklig-gleichschenklige Dreieck

Es gibt im rechtwinklig-gleichschenkligen Dreieck ebenfalls eine spiralförmige Anordnung. Der Grenzpunkt führt zu Fünfteln.

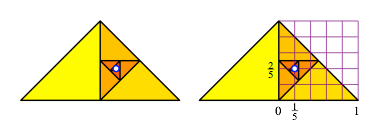
Spiralförmige Anordnung

Die Figur kann auch aus einem halben Origami Papier durch fortlaufendes Falten erreicht werden.

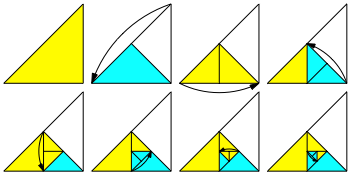
Faltprozess

Faltmodell

Die Thaleskreise der Teildreiecke verlaufen durch den Grenzpunkt, ebenso eine Art „Halbdiagonalen“.

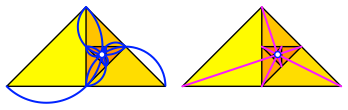
Thaleskreise. Halbdiagonalen

3.4 Der Sprung in den Raum

3.4.1 DIN-Quader

Wird ein Quader mit dem Kantenverhältnis halbiert, ergeben sich zwei Quader mit dem Kantenverhältnis . Diese sind ähnlich zum ursprünglichen Quader. Die folgende Abbildung zeigt einen DIN-Quader mit dem Kantenverhältnis im Vergleich zum Einheitswürfel.

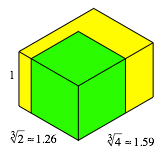
DIN-Quader und Einheitswürfel

Die folgende Abbildung zeigt eine Anordnung eines DIN-Quader-Sets analog zur klassischen Anordnung eines Sets von DIN-Rechtecken.

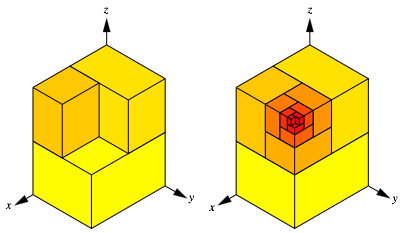
Anordnung

Während bei Rechtecken nur zwischen Querformat und Hochformat unterschieden werden kann, brauchen wir hier drei Anaordnungsformate. Dazu dient das beigefügte Koordinatensystem. Der erste Quader hat seine längsten Kanten in der x-Richtung, der zweite Quader hat seine längsten Kante in der y-Richtung und der dritte Quader in der z-Richtung. Der vierte Quader hat seine längsten Kanten wiederum in der x-Richtung.

Die Quader sind in einer Art räumlicher Spirale wie bei einer Wasserschnecke angeordnet.

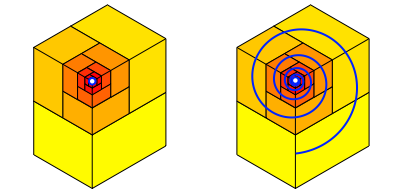
Wasserschnecke

Als Stimmungsbild reale DIN-Quader.

DIN-Kisten

3.4.2 DIN-Hyperquader

Im vierdimensionalen Raum ergeben sich durch

oder in anderer Schreibweise

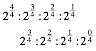
die Kanten zweier aufeinanderfolgender 4d-DIN-Hyperquader. George Pólya (1887-1985) hätte in dieser Situation allerdings von einer Verallgemeinerung durch Verwässerung gesprochen.

George Pólya

3.4.3 Gleichtemperierte 12-Ton-Stimmung

Wir verwässern weiter zum 12d-DIN-Hyperquader mit den Kantenlängen

Das hat man im Prinzip schon oft gesehen. Diese Zahlen stecken nämlich in den abnehmenden Abständen von Gitarrenbünden und in den Längen von Orgelpfeifen.

Orgelpfeifen. Dom zu Salzburg

Und man kann es darüber hinaus auch hören. Es sind die Frequenzverhältnisse der von Andreas Werckmeister (1645-1706) angeregten und in Bachs Werk Das Wohltemperierte Klavier demonstrierten gleichstufig temperierten Stimmung. Es ist das „demokratischste“ aller Stimmsysteme, da es alle Tonarten gleich behandelt und so Modulationen erleichtert.

Für das Stimmen eines Klaviers ist diese Theorie gut. Aber nur in erster Näherung. Ein so gestimmtes Instrument klingt nämlich noch keineswegs optimal. Das liegt daran, dass die Klaviersaitenschwingungen generell keine harmonischen Schwingungen sind. Die Rückstellkraft der Saite ist nämlich nicht proportional zur Auslenkung aus der Ruhelage. Die daraus entstehende „Inharmonizität“ hat nichts mit fehlerhafter Fertigung zu tun, sondern entsteht durch die Saitensteifigkeit.

Sie führt dazu, dass beispielsweise der erste Oberton des Kammertons a' = 440 Hz nicht mit 880 Hz schwingt, sondern etwas schneller, nämlich beinahe 881 Hz. Man würde es als zu tief und matt empfinden, wenn man die Oktave mathematisch nur auf  a'' = 880 Hz stimmen würde. Der Diskant muss je höher, desto stärker „gespreizt“ werden, damit der Klang brilliant wird. Der höchste Klavierton wird etwa 40 Cent höher gestimmt, als es der mathematischen Theorie entspricht. Der Bass hingegen wird abgesenkt. Auch bei einem guten Instrument ist Klavierstimmung ein Stück weit Geschmacksache.

Die Intervallgröße von einem Cent entspricht dabei dem Faktor .

3.5 Die Jakobsleiter

Und ihm träumte; und siehe, eine Leiter stand auf der Erde,

die rührte mit der Spitze an den Himmel, und siehe,

die Engel Gottes stiegen daran auf und nieder.

Gen 28, 11

Die Abbildung a) zeigt die ersten Sprossen der Jakobsleiter.

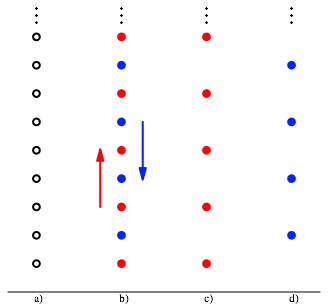
Jakobsleiter

Auf der einen Seite der Leiter steigen die Engel hinauf, auf der anderen Seite hinunter. Damit sie sich nicht gegenseitig auf den Füßen herumtreten, haben sie festgelegt, dass die aufsteigenden Engel nur die Sprossen mit ungeraden Nummern verwenden, die absteigenden nur die Sprossen mit geraden Nummern (Abb. b). Damit zerfällt die Jakobsleiter in zwei Teil-Jakobsleitern, die zur ursprünglichen Jakobsleiter ähnlich sind (Abb. c) und d). Wir haben also das Prinzip des DIN-Formates.

Der Reduktionsfaktor ist 2. Das Wort Reduktionsfaktor ist syntaktisch richtig, semantisch falsch, da Sprossenhöhne nicht reduziert, sondern verdoppelt wird. Unter dem Aspekt eines Fraktals ergibt sich die Mandelbrot-Dimension D (fraktale Dimension):

4 Würfel und Tetraeder

4.1 Kantenmodell des Würfels

Als Baumaterial dient Papier im DIN A6-Format. Geeignet ist Papier der Stärke 80 g/m², das vom Format A4 auf A6 zugeschnitten wird. Ebenfalls geht es mit dünnen Karteikarten.

Für jede Kante braucht es ein Papier.

Für den Faltprozess verwenden wir eine etwas festere A6-Karte als Faltlehre. Wir legen diese Faltlehre diagonal auf ein A6-Papier und falten die vorstehenden Ecken des darunterliegenden Papiers nach vorne über die Faltlehre. Dann entfernen wir die Faltlehre. Der Umriss des Papiers ist nun ein Rhombus mit dem spitzen Winkel .

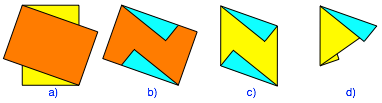
Faltvorgang

Nun falten wir die untere Spitze des Rhombus nach hinten unter die obere Spitze. Diese letzte Faltlinie wird zu einer Kante des Würfels. Was an dieser Kante noch vorsteht, kann zurückgebogen oder abgeschnitten werden. Damit haben wir unser Bauteil. Es hat die Form eines doppellagigen gleichschenkligen Dreiecks mit zwei Verbindungslaschen zum Einschieben in die Nachbarteile.

Die folgende Abbildung zeigt ein geöffnetes Bauteil von innen. Die Spitzen der beiden Rhomben-Hälften müssen vor dem Zusammenbau des Modells noch aufeinander gelegt werden. Diese Spitzen kommen alle in den Mittelpunkt des Würfels zu liegen. Die Seiten der Rhomben werden zu halben Raumdiagonalen des Würfels.

Wir benötigen 12 Bauteile. Beginnend mit drei verschieden farbigen A4-Papieren, die wir zu A6-Papieren vierteln, erhalten wir drei Sätze von je vier gleichfarbigen Bauteilen. Damit können wir den jeweils vier parallelen Würfelkanten dieselbe Farbe zuordnen.

Bauteil

Und nun kommt das Interessante, der Zusammenbau. Wir schieben jeweils eine Verbindungslasche zwischen die beiden gleichschenkligen Dreiecke des Nachbarbauteils. Dabei achten wir darauf, dass an jeder halben Raumdiagonale des Würfels drei Bauteile in den drei verschiedenen Farben zusammen kommen. Parallele Würfelkanten haben dieselbe Farbe.

Kantenmodell des Würfels

Es empfiehlt sich, den Zusammenbau schrittweise mit Büroklammern zu fixieren. An jeder Ecke des Würfels ergeben sich schließlich drei Büroklammern.

Wenn alles sitzt, können die Büroklammern schrittweise entfernt und durch eine Heftklammer mit dem Tacker ersetzt werden. Dabei hat man den Ehrgeiz, dass die Klammern symmetrisch eingebracht werden.

4.2 Kantenmodell des Tetraeders

Beim regelmäßigen Tetraeder haben wir den Ergänzungswinkel von auf 180°, also 109.4712°, als Winkel zwischen den vom Zentrum aus zu den Ecken verlaufenden Strecken. Daher kann analog zum Kantenmodell des Würfels ein Kantenmodell des Tetraeders gebaut werden.

Kantenmodell des Tetraeders

5 Das Silberne Rechteck

5.1 Ansetzen oder Abschneiden

Wir können zu einem DIN-Rechteck an der Schmalseite ein Quadrat ansetzen oder von einem DIN-Rechteck ein Quadrat abschneiden.

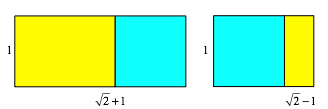
Quadrat ansetzen oder Quadrat abschneiden

Die folgende Abbildung zeigt das Summen- und das Differenzrechteck.

Summenrechteck und Differenzrechteck

Wir erhalten ein Summenrechteck mit dem Seitenverhältnis beziehungsweise ein Differenzrechteck mit dem Seitenverhältnis .

Wegen haben diese beiden Rechtecke dasselbe Seitenverhältnis. Ein solches Rechteck wird mit dem leicht esoterischen Namen Silbernes Rechteck bezeichnet, da es einige Eigenschaften ähnlich denen des Goldenen Rechtecks mit dem Seitenverhältnis des Goldenen Schnittes hat. Über den Goldenen Schnitt siehe (Walser, 2013).

5.2 Eigenschaften des Silbernen Rechtecks

Wir können zum Beispiel vom Silbernen Rechteck zwei Quadrate abschneiden. Es bleibt ein Silbernes Restrechteck übrig.

Zwei Quadrate abschneiden

Der Prozess kann iteriert werden, theoretisch ad infinitum.

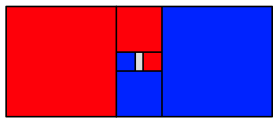
Iteration des Abschneidens

Wir können die Quadrate mit Viertelkreisen füllen. So entstehen zwei Spiralen.

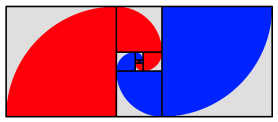
Spiralen

Wir können vier rechtwinklige-gleichschenklige Dreiecke (Geo-Dreiecke) so auslegen, dass ein Silbernes Umrissrechteck und ein Silbernes Lochrechteck entstehen.

Silberne Rechtecke als Umriss und als Loch

Auch dies kann iteriert werden.

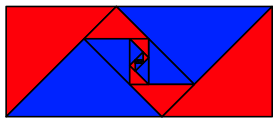
Iteration

5.3 Diagonalenschnittwinkel im Silbernen Rechteck

Die folgende Abbildung zeigt einen Beweis ohne Worte für den Sachverhalt, dass sich die Diagonalen im Silbernen Rechteck unter einem Winkel von 45° schneiden.

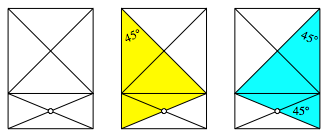
Diagonalenschnittwinkel im Silbernen Rechteck

6 Das regelmäßige Achteck

Der 45°-Winkel ist aber auch der Zentriwinkel im regelmäßigen Achteck. Daher erscheint das Silberne Rechteck im regelmäßigen Achteck.

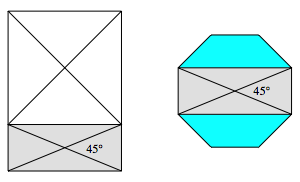
Silbernes Rechteck im regelmäßigen Achteck

Flächenmäßig macht das Silberne Rechteck genau die Hälfte des Achtecks aus. Dies kann mit einem Zerlegungsbeweis eingesehen werden.

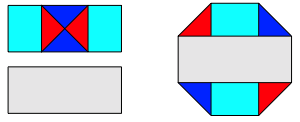
Teile-Ganzes-Beziehung

In der folgenden Zerlegung sind beide Silberne Rechtecke gleichermaßen zugeschnitten.

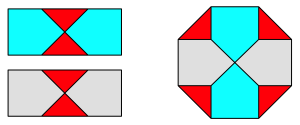
Zerlegungsbeweis

Der Zerlegungsbeweis kann noch subtiler gemacht werden, so dass ein Stern erscheint. Die Zerlegung des Achteckes hat von der Farbe abgesehen dieselben Symmetrien wie das Achteck selber.

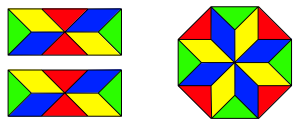
Zerlegungsbeweis mit Stern

Das Beispiel erinnert an die Legespiele nach Fröbel.

Fröbel-Stern

Weitere Zerlegungsbeweise zu diesem Thema siehe Link.

Wenn wir beim Stern zusätzlich zwei rechtwinklig gleichschenklige Dreiecke ansetzen passt die Figur in ein DIN-Rechteck.

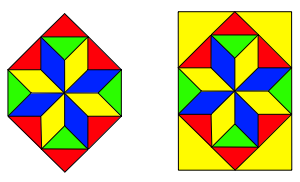
Einpassen ins DIN-Rechteck

6.1 Falten eines regelmäßigen Achtecks

Ein regelmäßiges Achteck kann aus einem DIN-Papier durch Falten hergestellt werden.

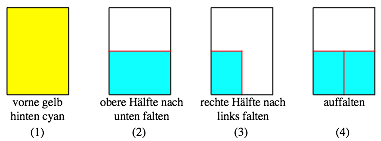
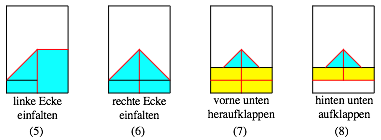
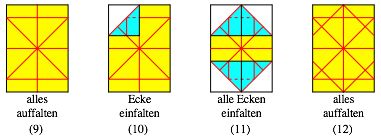
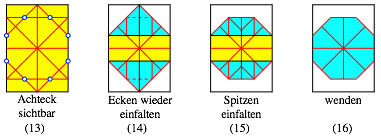
Falten eines Achteckes

Faltmodell

Natürlich können wir auch mit einem anderen Papier-Rechteck diesen Faltprozess durchführen. Wir erhalten dann ein zwar gleichwinkliges, aber nicht gleichseitiges Achteck. Die folgende Abbildung zeigt die Situation für das US Letter Format.

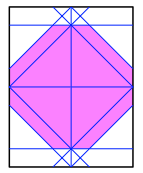
US Letter

7 Rechenaufgaben

7.1 Turm zu Papyron

7.1.1 Der Stapel

Wir zerlegen ein DIN-A4-Blatt in zwei DIN-A5-Blätter. Eines der beiden DIN-A5-Blätter zerlegen wir weiter in zwei DIN-A6-Blätter.

Nun legen wir eines der beiden DIN-A6-Blätter mittig auf das noch vorhandene DIN-A5-Blatt.

Das zweite DIN-A6-Blatt zerlegen wir ein zwei DIN-A7-Blätter und legen eines davon mittig auf das noch vorhandene DIN-A6-Blatt.

Und so weiter. Es entsteht ein Stapel.

7.1.2 Fragen

Frage 1: Ist dieser Stapel als „Pyramide“ oder als „Turm“ zu bezeichnen?

Frage 2: Wie hoch wird der Stapel?

7.1.3 Bearbeitung der Fragen

Die folgende Abbildung zeigt den Stapel von oben.

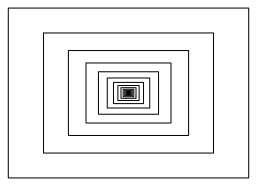
Stapel aus der Sicht von oben

Aus dieser Sicht lässt sich nicht entscheiden, ob wir es mit einer Pyramide oder einem Turm zu tun haben (Frage 1).

Die folgende Abbildung zeigt den Stapel von vorne. Die Papierdicke ist konstant, da ja alle Lagen aus demselben Papierblatt geschnitten sind.

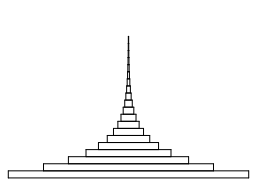
Sicht von vorne

Der Stapel ist als „Turm“ zu bezeichnen. Der Turm kann beliebig hoch werden. Die Seitenkonturen des Stapels sind um 90° gedrehte Exponentialkurven.

Bei einer Pyramide dürften die Seitenkonturen nicht gekrümmt sein. Dies wäre dann der Fall, wenn die Papierdicke abnehmen würde (folgende Abbildung). Das ist aber nicht möglich, da alle Teile aus demselben Papierblatt geschnitten sind.

Pyramide

Die Pyramide hätte – mit der Papierdicke d für die unterste Lage – die Gesamthöhe h:

8 Papier für die Welt

8.1 Fragen

Ein DIN-A4-Papier kann in zwei DIN-A5-Papiere zerschnitten werden oder in vier DIN-A6-Papiere oder in acht DIN-A7-Papiere oder ... (Abbildung).

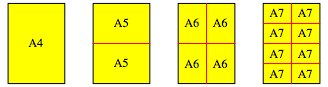
Zerlegungen

Welches Format muss gewählt werden, damit es für die ganze Menschheit reicht? Wie hoch wird der Stapel dieser Papiere? Welche Ausmaße hat ein einzelnes Blatt?

8.2 Bearbeitung

8.2.1 Format

Aus einem DIN-A4-Papier erhalten wir Papiere im Format DIN-An.

Die Weltbevölkerung beträgt 7.30 Milliarden Menschen (2015 / 16). Somit:

mit der technischen Lösung:

Wir müssen also das Format DIN-A37 wählen. Die genaue Anzahl Papier ist dann:

8.2.2 Stapelhöhe

Eine Packung von 500 Blatt Druckerpapier der Stärke 80g/m² ist ziemlich genau 5 cm dick. Das ergibt für ein einzelnes Blatt eine Dicke von 0.1 mm.

Ein Stapel von 8’589’934’592 Blättern ist somit etwa 859 km hoch.

8.2.3 Ausmaße

Wir rechnen im Hochformat.

Für die Höhe und die Breite des DIN-An-Papieres gilt:

Die Tabelle gibt die ersten numerischen Werte.

n	Höhe in [m]	Breite in [m]
0	1.189207115	0.8408964153
1	0.8408964150	0.5946035573
2	0.5946035575	0.4204482076
3	0.4204482076	0.2973017787
4	0.2973017788	0.2102241038
5	0.2102241038	0.1486508893
6	0.1486508894	0.1051120519
7	0.1051120519	0.07432544468
8	0.07432544469	0.05255602596
9	0.05255602593	0.03716272234
10	0.03716272234	0.02627801298
11	0.02627801297	0.01858136117
12	0.01858136117	0.01313900649
13	0.01313900648	0.009290680585
14	0.009290680586	0.006569503245
15	0.006569503242	0.004645340292
16	0.004645340293	0.003284751622
17	0.003284751621	0.002322670146
18	0.002322670146	0.001642375811
19	0.001642375810	0.001161335073
20	0.001161335073	0.0008211879056
21	0.0008211879053	0.0005806675365
22	0.0005806675366	0.0004105939528
23	0.0004105939526	0.0002903337683
24	0.0002903337683	0.0002052969764
25	0.0002052969764	0.0001451668841
26	0.0001451668842	0.0001026484882
27	0.0001026484882	0.00007258344207
28	0.00007258344208	0.00005132424410
29	0.00005132424408	0.00003629172103
30	0.00003629172104	0.00002566212205
31	0.00002566212204	0.00001814586051
32	0.00001814586052	0.00001283106102
33	0.00001283106102	0.000009072930257
34	0.000009072930260	0.000006415530512
35	0.000006415530510	0.000004536465129
36	0.000004536465130	0.000003207765256
37	0.000003207765255	0.000002268232564

Numerische Werte

Für n = 37 erhalten wir:

Wegen der Papierdicke von 0.1 mm erhalten wir ein sehr hohes Prisma.

Literatur

Walser, Hans(2013a): Der Goldene Schnitt. 6. Auflage. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.

Link

Zerlegungsbeweise:

www.walser-h-m.ch/hans/Miniaturen/A/Achteck2/Achteck2.pdf