Peter
Hilton, Jean Pedersen, Hans Walser
The
Faces of the Tri-Hexaflexagon
Mathematics Magazine, Vol. 70, No. 4, October
1997, 243-251
Introduction
Hexaflexagons were invented at Princeton in 1939 by Arthur H. Stone,
then a graduate student, now Professor Emeritus of Mathematics at the
University of Rochester. Martin Gardner gives an interesting account (see [1]) of StoneÕs work
and his collaboration with Bryant Tuckerman, then a graduate student and now a
retired research mathematician from IBM (Yorktown Heights, NY), the late
Richard P. Feynman, then a graduate student in physics and later a Nobel
Laureate, and John W. Tukey, then a young mathematics
instructor and now an Emeritus Professor at Princeton. It is interesting to remark that the diagrams Feynman devised for analyzing 6-faces
hexaflexagons were forerunners of the famous Feynman Diagrams in modern atomic physics. A description of how to
construct a 3-faces hexaflexagon may be found in any of the references [1]
through [4]. Further, a detailed description is given in [3, p. 63-74] of how
to construct hexaflexagons with 3n
faces without the use of straightedge or compass.
The
particular hexaflexagons we will consider in this article is the
tri-hexaflexagon[1],
so named because it has 3 faces; that
is, in any given state of the flexagon, one face (consisting of 6 equilateral
triangles) will be up, one face will be down, and one face will be hidden. Although
the orientation of the faces will vary from state to state, the same 6
triangles will always appear together on a face.
We will
show in this article how, by drawing a human visage on each face of the flexagon,
and using a different color for each face, we can keep track of all the possible
positions of the flexagon as it lies in a plane. We are thereby able to
discover that the set of motions of this flexagon which bring
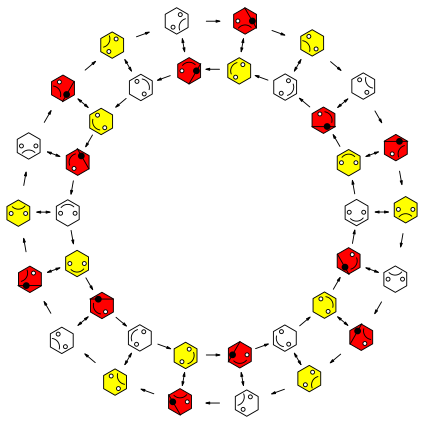
it into coincidence with itself constitutes the dihedral group 
.
1. How
to build the faced hexaflexagon
The
hexaflexagon is constructed from a strip of paper containing 10 equilateral
triangles[2] as shown in FIGURE 1. In
order that the final model will flex easily the fold lines between the
triangles should be creased firmly in both
directions.
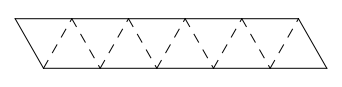
FIGURE 1: The
strip
Now we
decorate both sides of the strip as shown in FIGURE 2, where we make the bottom
surface of the strip visible by flipping the entire pattern piece over a horizontal axis as indicated by the
figure (where the vertices A, B, C, D
should correspond with the vertices 
, 
, 
, 
,
respectively, after you have flipped the piece over). Caution: Be careful here! Flipping the pattern piece over a vertical axis, and the decorating it as
shown does not produce the desired
flexagon.
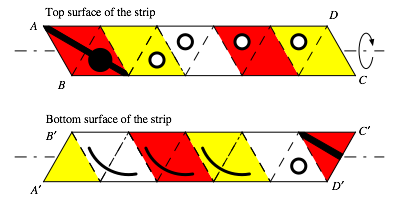
FIGURE 2: Decorating
the strip
Now we
suggest that you view the construction of the flexagon as a puzzle. Here are
some hints for constructing the flexagon with smiling (and frowning) faces.
(1) The first triangle of the upper
portion of the strip is ultimately glued to the last triangle on the bottom
portion (and it doesnÕt matter which one is on top of which). We suggest that
you attach these triangles with a paper clip at first, and save the actual
gluing until you are certain about the correctness of the construction.
(2) The completed flexagon should show
the visage of a smiling face, entirely in white, as you lay down as shown in
FIGURE 3(a). And when you flip the flexagon over, about a horizontal axis, it
should show the visage of a frowning face, entirely in yellow, oriented as
displayed in FIGURE 3(b).
(3) The strip that created the hexagon
contains three half-twists; thus like the Mšbius
band, it has only one surface (or side). Geometrically this means there will be
three slits on any face of this flexagon, symmetrically located at 120¡
intervals about its center. These slits are created by edges of the strip that
go from alternate vertices of the hexagon to its center as shown in both parts
of FIGURE 3.
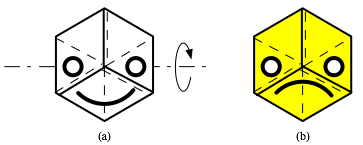
FIGURE 3:
The tri-hexaflexagon
From the
last hint above we know that the flexagon now has only one surface. After you
become proficient at manipulating your flexagon you may wish to verify with
your own model that the repetitive pattern of the three mouths, three right
eyes, and three left eyes in the colors white, red, yellow, respectively,
occurs as shown in FIGURE 4.
FIGURE 4:
The entire surface of the strip
2. The
happy group
First we
will always need to start with the flexagon in a standard initial position, that is, with the smiling white face up
and oriented precisely as shown in FIGURE 5(a).
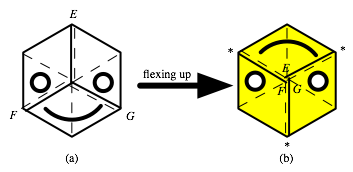
FIGURE 5:
The motion f, flexing up
Now we
assume 
and define the following motions:
the identity motion 1, which means we retain the
initial position,
f =
the motion of flexing up, starting from the initial position,
f n = the motion of flexing up n times, starting from the initial
position.
More
precisely, the motion f consists of
lifting the vertices of the hexagon, labeled E, F, and G (in FIGURE 5(a)) above the flexagon
until they meet, when the flexagon will come apart at the bottom and fall into
the shape of a new hexagon with the vertices E, F, and G at its
center. If this is done correctly (it is important not to rotate the flexagon
in either direction), you wll see the upside-down
smiling yellow face shown in FIGURE 5(b). Notice that the slits in the flexagon
have revolved 
of a turn. Thus, when you flex up the
second time you will have to bring the vertices marked with asterisks (*)
together above the flexagon. A simple way to remember what to do is that, in
each case, the vertex at the forehead of the human visage gets lifted to the
center (and it disappears as the motion is completed).
We now
follow the usual, obvious procedure of identifying a motion with its effect on
the initial position. When we do this we see that f 18 = 1, the identity motion.
Once you
have mastered the motions f n,
you may verify the sequence of motions which produce
the Happy Group shown in FIGURE 6; here we have adopted the identification
indicated above.
Since f 18 is the identity, we see
that the Happy Group is the cyclic group C18,
generated by f.
Next we define
flexing down. To describe this motion
, we
begin, as before, with the flexagon in the standard initial position shown[3] in FIGURE 7(a). Then 
means that we push the vertices of the
hexagon labeled H, J, and K downwards until they meet; at that
stage the flexagon will come apart at the top
and fall into the shape of a new hexagon with the vertices H, J, and K at its center,
but underneath the hexagon (this is
indicated by putting H, J, and K in parentheses in FIGURE 7(b)). If
this is done correctly, we will obtain the smiling pirate face in red as shown
in FIGURE 7(b).
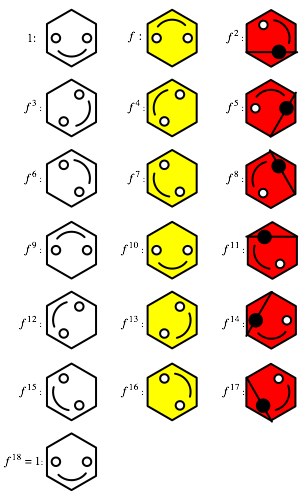
FIGURE 6:
The Happy Group
Just as
with the up-motions, it is important not to rotate the flexagon in either direction
as we flex it. Ta obtain 
, we simply repeat the process of flexing down n times (notice that when we flex down
the second time it is the vertices labeled with the asterisk (*) that come
together beneath the flexagon). It is interesting that, in flexing down, the
vertex at the forehead of the human visage moves up (as when flexing up), but in
this case the flexagon visibly splits across the forehead before it falls flat,
revealing the pirate.
FIGURE 7: The
motion 
, flexing down
Beginning
with the flexagon in the standard starting position, you may verify that 
yields the
same face as f 17 of
FIGURE 6. Thus 
. This means that, if you start with the position
indicated on the right of FIGURE 7 and flex down, you get the initial position.
In other words, flexing up is the inverse of flexing down (und vice versa), as
you might expect.
If you're
enjoying this you may check your flexing skill by reversing all of the steps of
the Happy Group in FIGURE 6.
3. The Entire Group
We realize
that the full group for this Hexagon must be larger than C18, because no frowning
faces ever appeared under the motions f n.
Cheerful as this situation is, it is plainly not
complete. Like everything in this world this Hexagon has good (happy)
and bad (unhappy) features. In order to get the entire group we certainly need
to have a motion that makes the unhappy faces visible. To achieve this we
introduce a new motion,
t =
turn over (so the rotation is about a horizontal
axis).
Thus, if we
begin with the Hexagon in the standard initial position and perform the motion t we will see a yellow frowning face
(see FIGURE 8).
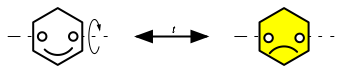
FIGURE 8: The
motion t, turning over
Obviously t is an involution, that is, t 2 = 1. FIGURE 9 shows that
the motion f t (meaning first do t, then do f) is not the same as t f
(meaning first do f, then do t). Check this (remembering that the flexagon
should be in the standard initial position, in both cases, when you start).
Thus we see that our new motion t
does not commute with f.
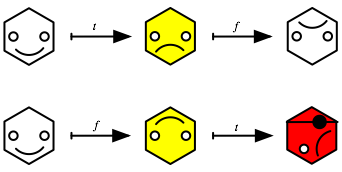
FIGURE 9: f t t f
We also
notice that when the pirate frowns his patch covers his left eye, instead of
the right one![4]
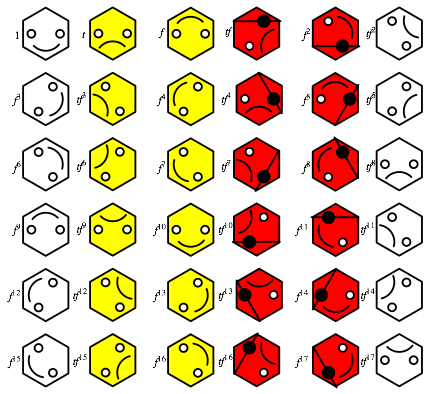
FIGURE 10:
The entire group
FIGURE 10
shows all the possibilities for f n
and t f n. Notice that the
first, third, and fifth columns are just the smiling faces from FIGURE 6. This
observation may give you an idea of an easy way to confirm that the visages in FIGURE
10 are correct.
We have
already seen that t f n f n t. However, since flexing
up, as viewed from above the Hexagon, is the same as flexing
down, as viewed from below the Hexagon, we have,
f n t = t f –n.
Thus we see
that the group generated by f and t has 36 elements and is therefore the fuIl group of motions of our flexagon. Since the generators
f, t satisfy the defining set of relations f 18 = 1, t 2
= 1, f t = t f –1, the group is the dihedral group D18, the group of symmetries
of the regular 18-gon (shown in FIGURE 11). The figure on the front cover shows
the effects of the group elements, where the single-headed arrows denote the f action and the double-headed arrows
denote the t action.
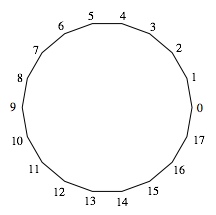
FIGURE 11:
The regular 18-gon
4. A Normal Subgroup
If we are
only interested in the different expressions on the faces of our Hexagon, without
respect to orientation, we have only 6 cases (as seen in FIGURE 12), instead of
36.
FIGURE 10
motivates the following argument. We obtain the group of motions of the unoriented faces by adding the relation f 3 = 1 to our group D18. The resulting quotient
group of D18 by the normal
subgroup generated by f 3
is then generated itself by F and t, subject to F 3 = 1, t 2
= 1, F t = t F –1. Here, F
is, of course, the image in the quotient group of f; and the quotient group is just the symmetric group S3.
FIGURE 12:
Expressions of the flexagon
5. A Challenge to the Reader
In [4] the
tri-hexaflexagon was discussed and the group S3 was obtained by using a flexagon where each of the 3
faces simply had different colors. In [2] the group D9 was obtained by a systematic labeling of the vertices
of the 6 triangles on each of the 3 faces of the tri-hexaflexagon. However, in
order to obtain the entire group D18,
it was necessary to introduce a finer method of distinguishing between the
different orientations of the faces, distinguishing between smiling and
frowning visages did the trick. The obvious next question to explore is whether
or not this, or some refinement of it, will help to identify the mathematical
structure of the hexa-hexa-flexagon
(with 6 faces). If we had a quick, or easy, answer to this question we wouldn't
be stopping here!
REFERENCES
1. Martin
Gardner. The Scientific
American Book of Mathematical Puzzles and Diversions. Simon and Schuster, New York, NY, 1959.
2. Michael Gilpin,
Symmetries of the trihexaflexagon. Mathematics Magazine 49, No. 4 (1976),
189-192.
3. Peter
Hilton and Jean Pedersen: Build Your Own Polyhedra. Addison-Wesley, Menlo Park, CA, 1994.
4. Jean Pedersen.
Sneaking up on a group. Two-year
College Mathematics Journal 3 (1972), 9-12.