Hans Walser, [20180529]

Zylinderstapel

1     Worum geht es?

Stehende Zylinder mit dem Radius  und der Hšhe 1 sollen so gestapelt werden, dass ihre Mittelpunkte ein flŠchenzentriertes kubisches Punktgitter ergeben.

Die Zylinder kšnnen als ãInzylinderÒ von EinheitswŸrfeln gesehen werden.

2     Quadratische Basis

2.1    Berechnung

Die Abbildung 1 zeigt das Minimalmodell mit quadratischer Basis der Stapelung.

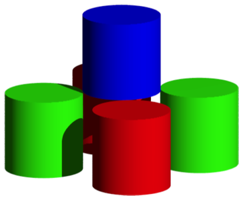
Abb. 1: Quadratische Basis

Die Bedingung fŸr ein flŠchenzentriertes kubisches Punktgitter verlangt, dass die AbstŠnde zwischen den Zylindermittelpunkten alle gleich lang sind.

Die durch die AbstŠnde x gebildete Pyramide hat die Hšhe 1. Damit erhalten wir die Bedingung:

 

                                                                                                       (1)

 

Dies fŸhrt zur positiven Lšsung:

 

                                                                                                                             (2)

 

Wir sehen in der Abbildung 1, dass die Zylinder nicht eigentlich gestapelt sind. Der blaue Zylinder sitzt auf den Kanten der darunter liegenden Zylinder und wŸrde bei Wirken der Schwerkraft zwischen den roten und grŸnen Zylindern hinunterrutschen, es sei denn, man stelle einen StŸtzzylinder darunter.

2.2    Pyramide

Die Abbildung 2 zeigt eine grš§ere Basis und die Pyramide.

Abb. 2: Pyramide

Die Abbildung 3 zeigt die Situation von vorne und von oben. Bei der Abbildung 3a meinen wir, eine Wand von aufgestapelten Dosen wie beim Dosenschie§en an der Geburtstagsparty zu sehen. TatsŠchlich liegt aber schon die zweitunterste Reihe nach hinten versetzt, wie aus der Abbildungen 2b und 3b ersichtlich ist.

Abb. 3: Von vorne und von oben

2.3    Umkugel

Wir legen um die Zylinder (Abb. 4a) die Umkugel (Abb. 4b).

Abb. 4: Umkugel

Das hat zur Folge dass die nun vergrš§erten Figuren nicht mehr an den Kanten abrutschen kšnnen. Die Umkugeln haben den Durchmesser . Das hei§t dass sie sich gegenseitig berŸhren. Wir erhalten die dichteste Kugelpackung (Abb. 5).

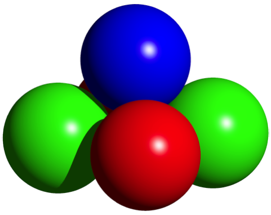
Abb. 5: Dichteste Kugelpackung

3     Dreieckige Basis

3.1    Berechnung

Die Abbildung 6 zeigt das Minimalmodell fŸr den Fall einer dreieckigen Basis von oben. Die Zylinder sind nun echt aufeinandergestapelt.

Abb. 6: Dreieckige Basis

Die Zylindermittelpunkte mŸssen die Ecken eines regelmŠ§igen Tetraeders bilden (Abb. 6b). Dieser Tetraeder hat die Hšhe 1. FŸr die rote KantenlŠnge x des Tetraeders ergibt sich:

 

                                                                                                             (3)

 

3.2    Kugelpackung?

Wegen  durchschneiden sich die Umkugeln der Zylinder. FŸr eine Kugelpackung mŸssen wir mit kleineren Kugeln arbeiten, welche die Zylinder durchschneiden (Abb. 7).

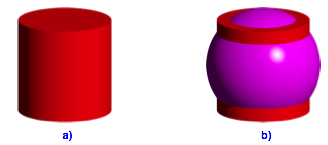
Abb. 7: Kugel fŸr Kugelpackung

3.3    Tetraeder

Die Abbildung 7 zeigt die Basis und den Tetraeder.

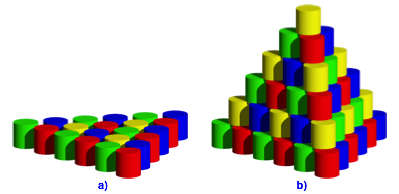
Abb. 7: Basis und Tetraeder

Die Abbildung 8 zeigt die Situation von der Seite und von oben.

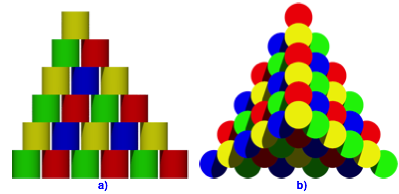
Abb. 8: Von der Seite und von oben

Website

Hans Walser: WŸrfelstapel (abgerufen 30.05.2018):

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelstapel/Wuerfelstapel.htm