Hans Walser, [20220611]

Zwischenwinkel

Anregung: LG, V.

1 Worum geht es?

Folge von Zwischenwinkel in wachsenden Dimensionen. Frage der Konvergenz

2 Einleitung und Problemstellung

An einer mündlichen Prüfung wählten die Kandidat*innen bei zwei Vektoren (zur Berechnung des Zwischenwinkels) in der Ebne oder im Raum sehr oft die beiden Beispiele

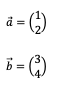
Beziehungsweise

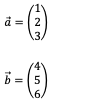
Daraus ergibt sich folgende allgemeine Frage: Wie groß ist der Zwischenwinkel der beiden n-dimensionalen Vektoren:

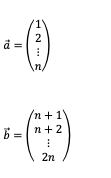
3 Beispiel

In der Ebene suchen wir den Zwischenwinkel zwischen den Vektoren (Abb. 1):

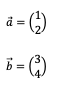
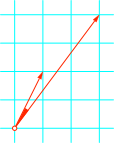
Abb. 1: Zwischenwinkel?

Der Zwischenwinkel beträgt etwa 10.30484653° (Tab. 1).

Da alle unsere Vektoren in der ersten Hälfte des eindimensionalen, im ersten Quadranten des ebenen, im ersten Oktanten des räumlichen Koordinatensystems etc. spielen, sind alle Winkel spitz.

4 Bearbeitung

Wir berechnen den Zwischenwinkel γ mit Hilfe des Skalarproduktes:

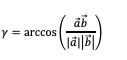
Für das Skalarprodukt finden wir:

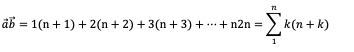
Nun ist:

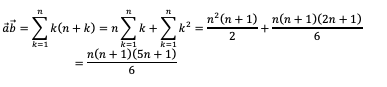
Weiter ist:

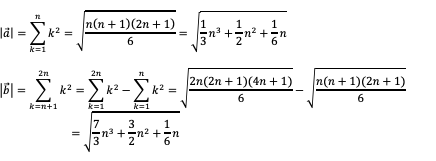
Daraus ergibt sich:

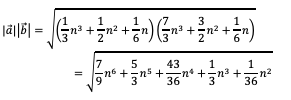
Somit erhalten wir für den Zwischenwinkel γ:

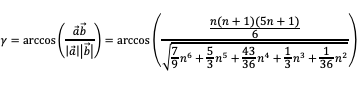
Die Tabelle 1 gibt die ersten 15 Werte.

n	Zwischenwinkel γ
1	0°
2	10.30484653°
3	12.93315452°
4	14.33517020°
5	15.21441405°
6	15.81879582°
7	16.26020471°
8	16.59688258°
9	16.86221599°
10	17.07674123°
11	17.25379319°
12	17.40241088°
13	17.52894028°
14	17.63796826°
15	17.73289307°

Tab. 1: Zwischenwinkel

5 Grenzwert

In der Tabelle 1 sehen wir, dass der Zwischenwinkel γ zunächst stark, dann aber immer weniger zunimmt. Gibt es eine obere Schranke?

Um dies zu klären, formen wir die Zwischenwinkelformel um und vereinfachen (Ausmultiplizieren und Kürzen):

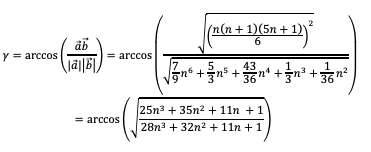
Bei dieser Umformung werden allerdings allfällige stumpfe Winkel in ihre spitzen Ergänzungswinkel auf 180° umgeformt. Wir wissen aber, dass ohnehin nur spitze Winkel im Spiel sind.

Der Radikand

strebt für wachsendes n gegen

Somit erhalten wir für den Zwischenwinkel γ den Grenzwert:

Die Abbildung 2 illustriert die Situation.

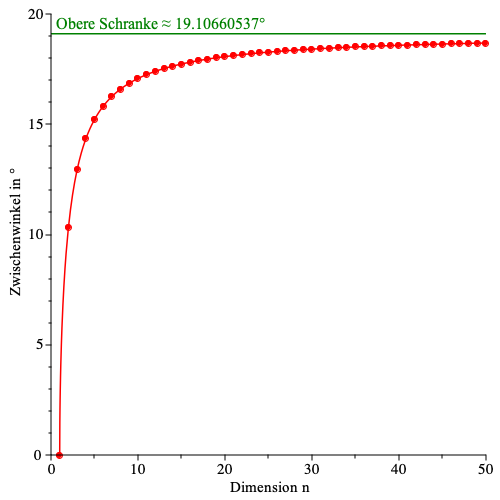
Abb. 2: Zwischenwinkel und Grenzwert

6 Vektorlängen

In der Tabelle 2 sind die Längen der beiden Vektoren eingetragen sowie deren Längenverhältnis. Neben dem trivialen Fall n = 1 haben wir auch für n = 7 ein rationales Längenverhältnis.

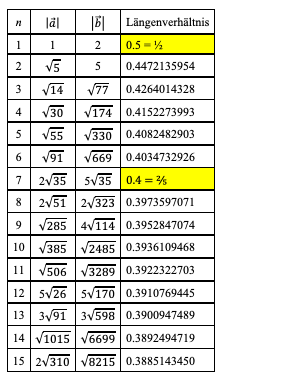
Tab. 2: Vektorlängen

Wir vermuten, dass es auch für das Längenverhältnis einen Grenzwert gibt.

Aus den Berechnungen der Vektorlängen folgt mit einigen Umformungen (Expandieren und Kürzen)

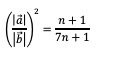
Für wachsendes n strebt dieser Wert gegen ⅐. Somit haben wir für das Längenverhältnis der beiden Vektoren den Grenzwert:

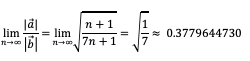
Dieser Grenzwert ist eine untere Schranke. Die Abbildung 3 illustriert den Sachverhalt.

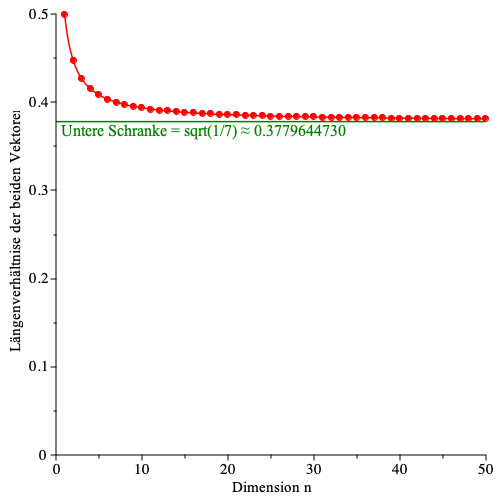
Abb. 3: Längenverhältnisse der beiden Vektoren

7 Grenzfigur

Es gibt somit eine Grenzfigur mit dem Grenzwert des Längenverhältnisses der beiden Vektoren und dem Grenzwert des Zwischenwinkels. Diese Grenzfigur ist unendlich groß, aber wir können seine Form zeichnen (Abb. 4). Die Figur spielt in einem Raum der Dimension unendlich.

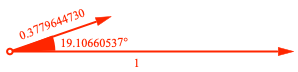
Abb. 4: Grenzfigur

Der Flächeninhalt des durch die beiden Vektoren aufgespannten Grenzdreiecks mit der normierten Länge 1 für den längeren Vektor ist gleich dem Flächeninhalt des gleichseitigen Dreieckes mit der Seitenlänge sqrt(1/7) (Abb. 5).

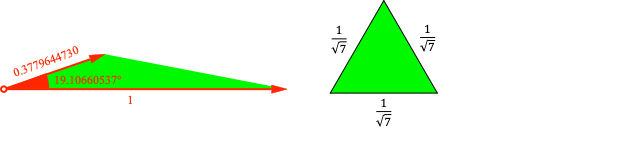
Abb. 5: Flächenvergleich

Auffallend ist das mehrfache Auftreten von sqrt(7) im Grenzfall.