Hans Walser, [20110420a]
Zwei Quadrate
Wir setzen zwei
Quadrate neben einander und zeichnen dann geeignete Geraden. Es entstehen ein
Schnittpunkt von drei Geraden sowie ein rechtwinkliges Dreieck. Schlie§lich kommen
auch Umkreise ins Spiel.
Die Beweise kšnnen mit
elementaren Mitteln gefźhrt werden. Beweisškonomisch ist es zwar sinnvoll (und
einfacher), gleich die allgemeinen FŠlle (Abschnitt 6) anzugehen. Im Sinne
einer Kompetenzkumulation empfiehlt es sich aber, die Beispiele Schritt fźr
Schritt zu beweisen.
1
Die beiden Quadrate
Zu zwei festen Punkten A und B
zeichnen wir die zugehšrige Gerade und wŠhlen darauf einen Punkt D. Dann ergŠnzen wir zu den beiden Quadraten ADSQ und DBPR
(Abbildung 1).
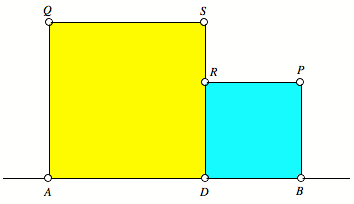
Abb. 1: Die beiden
Quadrate
Falls D au§erhalb der Strecke AB gewŠhlt wird, zeichnen wir die beiden Quadrate konsistent
orientiert. Die Abbildung 2 zeigt eine solche Situation.
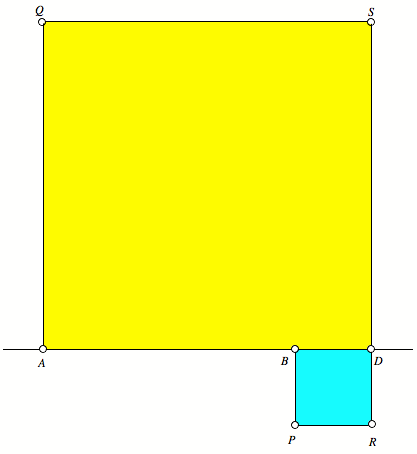
Abb. 2: D au§erhalb der Strecke AB
2
Ein Schnittpunkt
Die drei Geraden AP, BQ
und RS sind kopunktal (Abb. 3).
Das hei§t, dass die drei Geraden durch denselben Punkt verlaufen. Diesen
Schnittpunkt nennen wir T. Wer
findet den einfachsten Beweis?
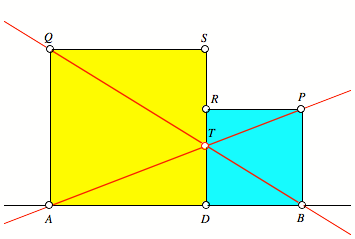
Abb. 3: Drei kopunktale
Geraden
3
Eine Parabel
Nun lassen wir A und B
fest, variieren aber den Punkt D
auf der Geraden AB. Dann beschreibt
der Punkt T eine Parabel (Abb.
4).
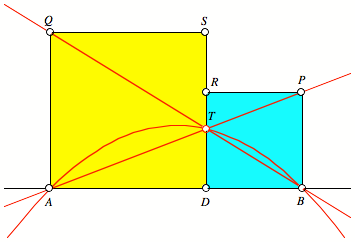
Abb. 4: Parabel
4
Noch ein Schnittpunkt
Die Geraden AR und BS
sowie der Thaleskreis źber der Strecke AB sind kopunktal (Abb. 5). Den Schnittpunkt nennen wir C.
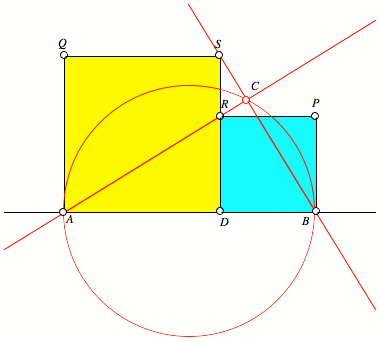
Abb. 5: Noch ein
Schnittpunkt
Wir erhalten also ein rechtwinkliges Dreieck ABC. †ber AktivitŠten im rechtwinkligen Dreieck siehe [Mźller-Sommer 2008].
5
Winkelhalbierende
Die Winkelhalbierenden
des rechten Winkels bei C verlaufen
durch D beziehungsweise P und Q
(Abb. 6).
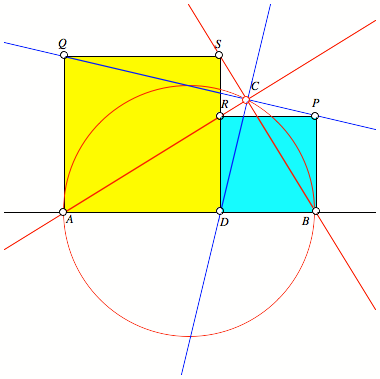
Abb. 6:
Winkelhalbierende
Das hei§t, dass der
Punkt C auch auf den Umkreisen der
beiden Quadrate liegt (Abb. 7).
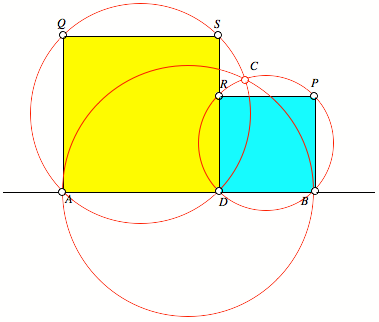
Abb. 7: Zwei Umkreise
und ein Thaleskreis
6
Verallgemeinerungen
Verallgemeinerung
durch VerwŠsserung (George P—lya)
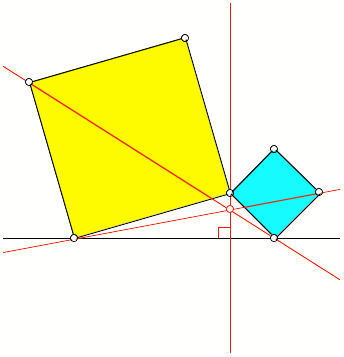
Abb. 8: Dreieck mit
aufgesetzten Quadraten
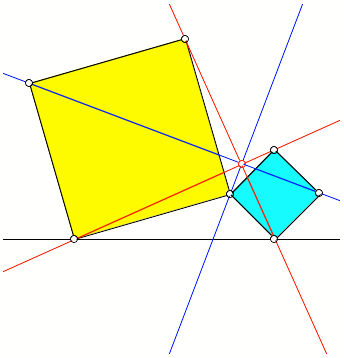
Abb. 9: Vier Geraden unter
Winkeln von 45ˇ
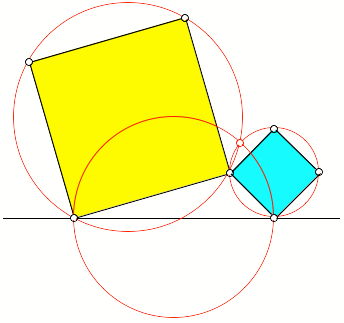
Abb. 10: Drei Kreise
durch einen Punkt
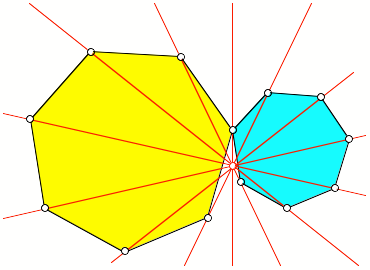
Abb. 11: Sieben auf
einen Punkt
Vgl. [Walser 2004], S.
163f.
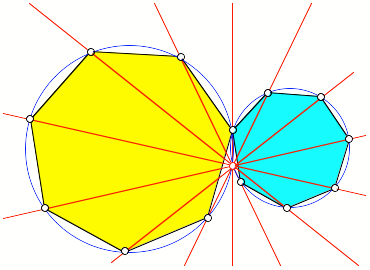
Abb. 12: Beweistipp
Literatur
[Mźller-Sommer 2008] Mźller-Sommer, Hartmut: Das Baustoff-Bauplan-Prinzip. Praxis der Mathematik in der Schule, PM 50 (2008/19) S. 27-32.
[Walser 2004] Walser, Hans: 99 Schnittpunkte. Beispiele – Bilder – Beweise. Edition am Gutenbergplatz, Leipzig 2004. ISBN 3-937219-10-2