1 Worum geht es?

Flächen Dreiecke im Trapez. Zerlegungsgleichheit. Affine Transformationen.

2 Dreiecke im Trapez

Die beiden Trapezdiagonalen unterteilen das Trapez in vier Dreiecke (Abb. 1).

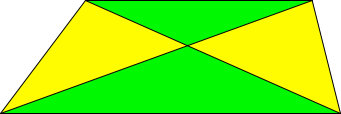
Abb. 1: Unterteilung in vier Dreiecke

Die beiden Dreiecke an den Parallelseiten (grün) sind ähnlich (formgleich). Nachweis durch Wechselwinkel an Parallelen.

Die beiden Dreiecke an den Schrägseiten (gelb) sind flächengleich. Rechnerischer Nachweis: Gelb links plus grün unten einerseits und gelb rechts plus grün unten andererseits können je als neues Dreieck gesehen werden. Diese beiden Dreiecke haben dieselbe Grundlinie und dieselbe Höhe, sind also flächengleich. Nach Abschneiden des grünen Dreiecks sind auch die beiden gelben Restdreiecke flächengleich.

3 Zerlegung

Die Abbildung 2 zeigt eine gemeinsame Zerlegung der beiden flächengleichen Dreiecke.

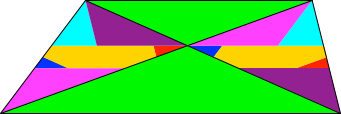
Abb. 2: Gemeinsame Zerlegung

4 Affine Invarianz

Die Figur ist invariant gegenüber affinen Abbildungen.

In der Abbildung 3 ist die Breite unverändert, aber die Figur in die Höhe gezogen.

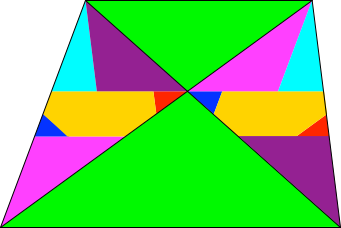
Abb. 3: Überhöhung

Entsprechende Teilfiguren sind immer noch kongruent. Wir haben immer noch eine gemeinsame Zerlegung.

Die Abbildung 4 zeigt eine allgemeine affine Transformation.

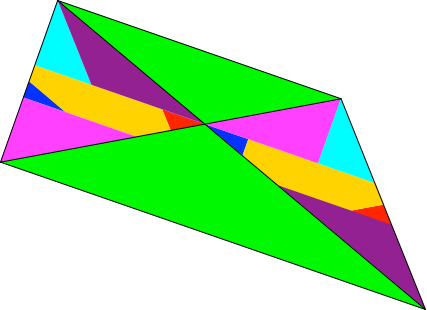
Abb. 4: Affine Transformation

Die Abbildung 5 zeigt eine Scherung.

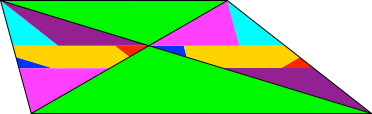
Abb. 5: Scherung

Die Invarianz kann wie folgt gezeigt werden: Entsprechende kongruente Teilfiguren sind entweder parallel zueinander (hellblau, gold) oder punktgespiegelt (pink, magenta, rot, blau). Beide Lagebeziehungen sind invariant gegenüber affinen Transformationen. Hintergrund: Affine Transformationen sind parallelenerhaltend und flächenverhältniserhaltend).