1 Worum geht es?

Illustration des Satzes von Xavier mit Spiralen.

2 Der Satz von Xavier

In einer Kugel wählen wir symmetrisch zum Mittelpunkt zwei gelbe horizontale Schnittkreise (Abb. 1a). Die geografische Breite der Schnittkreise ist beliebig, im Beispiel der Abbildung 1 wurde ±30° gewählt.

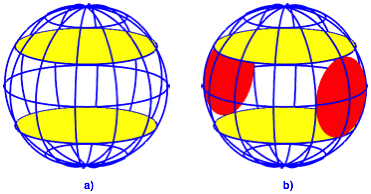
Abb. 1: Schnittkreise in der Kugel

Nun zeichnen wir zwei rote vertikale Schnittkreise, welche die gelben horizontalen Kreise berühren (Abb. 1b).

In dieser Situation gilt der Satz von Xavier:

Die Flächensumme der vier Schnittkreise ist doppelt so groß wie die Querschnittsfläche der Kugel und halb so groß wie die Oberfläche der Kugel.

Der rechnerische Beweis verwendet den Satz des Pythagoras.

3 Spiralen

Wir approximieren die Kreisscheiben durch aufgewickelte Seile, also durch Spiralen.

Die Abbildung 2a zeigt eine einzelne solche Doppelspirale. Sie ist in der einen Ebene auf- und in der anderen Ebene abgewickelt.

Die Abbildung 2b zeigt alle vier benötigten Spiralen. Es sind in jeder Ebene je zwei Spiralen ineinander gewickelt.

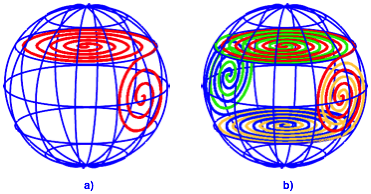
Abb. 2: Doppelspiralen

In der Animation 1 sehen wir das simultane Auf- und Abwickeln. Da immer gleich viel auf- wie abgewickelt wird, ist die Flächensumme der vier Kreisscheiben invariant. Aus dem Sonderfall der Doppelscheibe in der Äquatorebene ergibt sich der Vergleich mit der Querschnittsfläche der Kugel.