Hans Walser, [20090509a]
Wurzeln aus Matrizen
1
Worum es geht
Zu einer gegebenen
2,2-Matrix A suchen wir 2,2-Matrizen B mit der Eigenschaft: ![]() . Wir suchen also Quadratwurzeln der Matrix A.
. Wir suchen also Quadratwurzeln der Matrix A.
2
Quadrieren
Wenn wir eine
quadratische 2,2-Matrix B mit den
Eigenwerten ![]() und
Eigenvektoren
und
Eigenvektoren ![]() quadrieren,
erhalten wir eine Matrix
quadrieren,
erhalten wir eine Matrix ![]() mit denselben Eigenvektoren und den Eigenwerten
mit denselben Eigenvektoren und den Eigenwerten ![]() .
.
Beweis: Aus ![]() ergibt sich:
ergibt sich: ![]() .
.
3
Quadratwurzeln
Wir gehen davon aus,
dass die Matrix A zwei verschiedene
Eigenwerte ![]() und
und ![]() hat. (Der Fall
hat. (Der Fall ![]() ist recht
kompliziert.) Dazu gehren die
Eigenvektoren
ist recht
kompliziert.) Dazu gehren die
Eigenvektoren ![]() und
und ![]() . Um eine Matrix B
mit
. Um eine Matrix B
mit ![]() zu finden,
bestimmen wir deren Eigenwerte
zu finden,
bestimmen wir deren Eigenwerte ![]() aus
aus ![]() . Man beachte, dass es hier vier verschiedene
Vorzeichenkombinationen geben kann. Dann bestimmen wir B aus den Eigenwerten
. Man beachte, dass es hier vier verschiedene
Vorzeichenkombinationen geben kann. Dann bestimmen wir B aus den Eigenwerten ![]() und den
Eigenvektoren
und den
Eigenvektoren ![]() .
.
4
Beispiel
Wir bearbeiten die
Matrix A:
![]()
4.1
Eigenwerte und Eigenvektoren der Matrix A
Die charakteristische
Gleichung fr die Eigenwerte ist ![]() . Daraus erhalten wir
. Daraus erhalten wir ![]() und damit die
Eigenwerte
und damit die
Eigenwerte ![]() und
und ![]() . Zum Eigenwert
. Zum Eigenwert ![]() muss ein
Eigenvektor
muss ein
Eigenvektor ![]() die folgende
Bedingung erfllen:
die folgende
Bedingung erfllen:
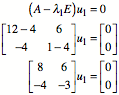
Eine mgliche Lsung
ist:
![]()
Analog finden wir fr ![]() eine mgliche
Lsung:
eine mgliche
Lsung:
![]()
4.2
Wurzelmatrix
Die gesuchte
Wurzelmatrix B hat also die Eigenwerte ![]() und
und ![]() . Es gibt vier Vorzeichenkombinationen. Wir bearbeiten
exemplarisch den Fall plus-plus,
also
. Es gibt vier Vorzeichenkombinationen. Wir bearbeiten
exemplarisch den Fall plus-plus,
also ![]() und
und ![]() . Die Eigenvektoren sind dieselben wie die der Matrix A.
. Die Eigenvektoren sind dieselben wie die der Matrix A.
4.2.1 Erster Lsungsweg
Fr die Matrix B machen wir den Ansatz:
![]()
Damit muss gelten: ![]() und
und ![]() .
.
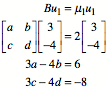 und
und 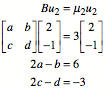
Fr das
Gleichungssystem
![]()
ergibt sich die Lsung:
![]() , also die Matrix B:
, also die Matrix B:
![]()
4.2.2
Zweiter Lsungsweg
U sei die Matrix mit den Spaltenvektoren ![]() und
und ![]() . Dann gilt:
. Dann gilt:
![]()
Hintergrund: Die Matrix
![]() bringt die Eigenvektoren auf die Koordinatenachsen.
Dann wird in Richtung der beiden Koordinatenachsen mit
bringt die Eigenvektoren auf die Koordinatenachsen.
Dann wird in Richtung der beiden Koordinatenachsen mit ![]() beziehungsweise
beziehungsweise ![]() gestreckt. Die Matrix U schlie§lich bringt die gestreckten Vektoren wieder in
die Richtung der ursprnglichen Eigenvektoren. Die Zusammensetzung ist aber
genau das, was die Matrix B
bewirken soll.
gestreckt. Die Matrix U schlie§lich bringt die gestreckten Vektoren wieder in
die Richtung der ursprnglichen Eigenvektoren. Die Zusammensetzung ist aber
genau das, was die Matrix B
bewirken soll.
4.3
Lineare Abbildung
In der folgenden Figur
haben wir ein grnes Urbild. Magenta ist das Bild bei der linearen Abbildung
mit der Matrix B, rot das Bild bei der
linearen Abbildung mit der Matrix ![]() . Blau sind die Geraden in den Richtungen der Eigenvektoren
eingezeichnet.
. Blau sind die Geraden in den Richtungen der Eigenvektoren
eingezeichnet.
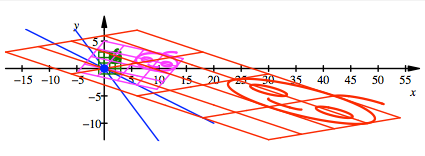
Urbild, Zwischenbild und
Bild
5
MuPAD
Das folgende
MuPAD-Programm liefert alle vier Vorzeichenkombinationen bei den Eigenwerten
von B.
5.1
Erster Lsungsweg
Matr:= Dom::Matrix(): // Eigenwerte und Eigenvektoren A
A := Matr([[12, 6], [-4, 1]]);
B := Matr([[a, b], [c, d]]):
EA := linalg::eigenvectors(A);
u:=j->EA[j][3][1]:
lambda:=j->EA[j][1]:
for p from 0 to 1 do // Vorzeichenkombinationen
for q from 0 to 1 do
mu[p,q,1]:=(-1)^p*sqrt(lambda(1)):
mu[p,q,2]:=(-1)^q*sqrt(lambda(2)):
end_for:
end_for:
Gleichung:=(p,q)->{(((B*u(j))[i]=mu[p,q,j]*u(j)[i])$j=1..2)$i=1..2}:
for p from 0 to 1 do // Berechnen der Matrix B
for q from 0 to 1 do
s:=solve(Gleichung(p,q), {a,b,c,d}):
B1:=Matr([[s[1][1][2],
s[1][2][2]], [s[1][3][2], s[1][4][2]]]):
print(Typeset, B1):
end_for:
end_for:
Zur Matrix A
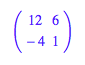
erhalten wir die
Eigenwerte mit Vielfachheit und die Eigenvektoren
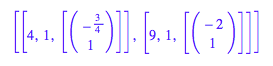
und der Reihe nach die
zu den verschiedenen Vorzeichenkombinationen passenden Lsungen:

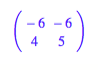
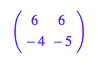
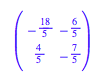
5.2
Zweiter Lsungsweg
Matr:= Dom::Matrix(): // Eigenwerte und Eigenvektoren A
A := Matr([[12, 6], [-4, 1]]);
EA := linalg::eigenvectors(A):
u:=j->EA[j][3][1]:
lambda:=j->EA[j][1]:
U:=Matr([[EA[1][3][1][1], EA[2][3][1][1]],
[EA[1][3][1][2],
EA[2][3][1][2]]]);
for p from 0 to 1 do // Vorzeichenkombinationen
for q from 0 to 1 do
mu[p,q,1]:=(-1)^p*sqrt(lambda(1)):
mu[p,q,2]:=(-1)^q*sqrt(lambda(2)):
end_for:
end_for:
for p from 0 to 1 do // Berechnen der Matrix B
for q from 0 to 1 do
Di:=Matr([[mu[p,q,1],
0], [0, mu[p,q,2]]]):
B:=U*Di*U^(-1):
print(Typeset, B):
end_for:
end_for:
Zur Matrix A
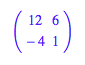
erhalten wir die Matrix
U aus den Eigenvektoren
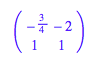
und der Reihe nach die
zu den verschiedenen Vorzeichenkombinationen passenden Lsungen:

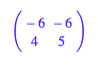
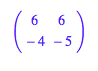
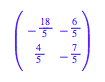
6
Abbildungen
Im Folgenden zu jeder
Lsung die Abbildungen:
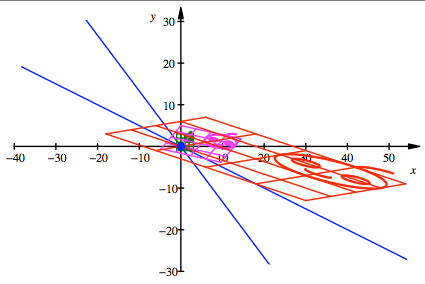
Erste Lsung
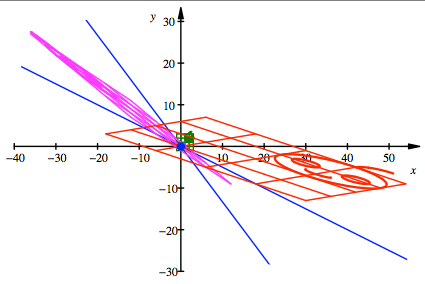
Zweite Lsung
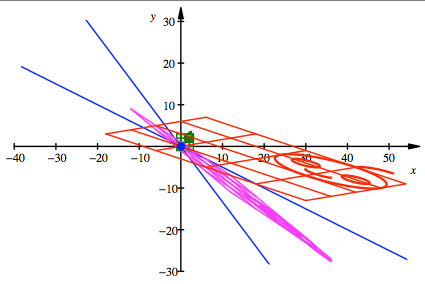
Dritte Lsung
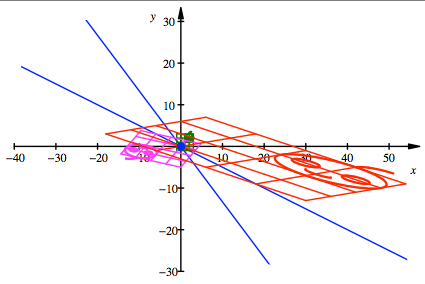
Vierte Lsung
Die magenta
Zwischenbilder sehen unterschiedlich aus. In der ersten und vierten Lsung sind
sie gleich orientiert (Locke beachten) wie das Urbild und das Endbild, in der
zweiten und dritten Lsung sind sie entgegengesetzt orientiert.
7
Die Drehung
Als interessantes
Beispiel behandeln wir die Drehmatrix A:
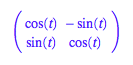
Aus geometrischen
Grnden ist die Drehung um den halben Winkel sicher eine Lsung:
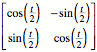
Fr die Matrix U der Eigenvektoren liefert MuPAD:
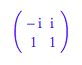
MuPAD liefert als erste
Lsung:
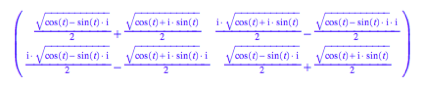
Dies ist tatschlich
die aus geometrischen Grnden gefundene Lsung, es gengt, die erste Zeile zu
kontrollieren:
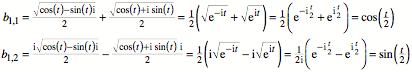
MuPAD liefert als
zweite Lsung:
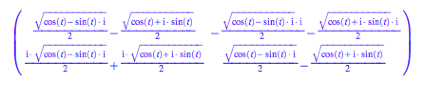
Diese Matrix kann
umgeformt werden zu:
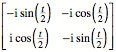
Kontrolle:
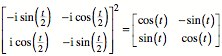
Die dritte Lsung sieht
so aus:
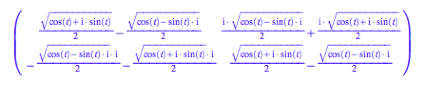
Diese Matrix kann
umgeformt werden zu:
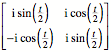
Fr die vierte Lsung
liefert MuPAD:
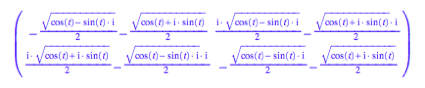
Diese Matrix kann
umgeformt werden zu:
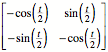
Es ist:
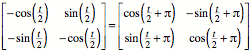
Damit ist es aus geometrischen
Grnden klar, dass es sich um eine Wurzel der Drehmatrix handelt.