Hans Walser, [20230612]

Winkelhalbierendenabschnitte

Anregung: Helmut Mallas, Flensburg

1 Worum es geht

Ganzzahlige Spielerei in der Dreiecksgeometrie. Inkreis. Pythagoreische Dreiecke.

2 Problemstellung

Gesucht ist ein Dreieck mit ganzzahligen Seitenlängen a, b, c, ganzzahligem Inkreisradius r und ganzzahligen Abschnitten von den Ecken zum Mittelpunkt des Inkreises.

3 Beispiel

Im Beispiel der Abbildung 1 ist: AI = 275, BI = 429, CI = 325, r = 165, a = 676, b = 500, c = 616.

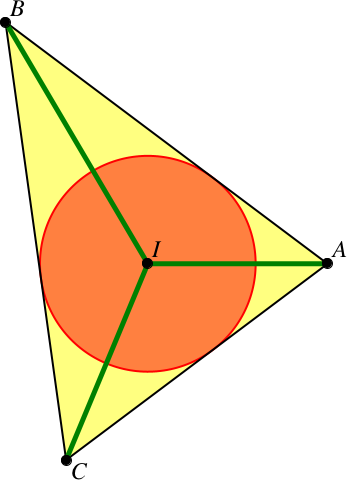
Abb. 1: Beispiel

4 Analyse des Beispiels

Wir können das Dreieck in sechs rechtwinklige Dreiecke zerlegen, welche paarweise spiegelbildlich sind (Abb. 2). Die Hypotenusen der Dreiecke sind die Abschnitte AI, BI und CI, die eine Kathete ist der Inkreisradius r. Die jeweils zweite Kathete ist ebenfalls ganzzahlig. Die sechs Dreiecke sind pythagoreische Dreiecke.

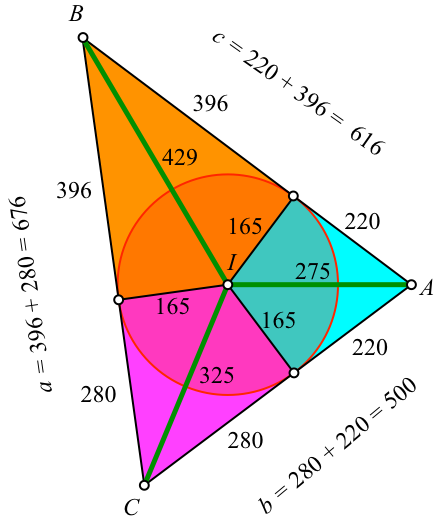
Abb. 2: Analyse des Beispiels

Die hellblauen Dreiecke haben das Seitenverhältnis 165:220:275 = 3:4:5. Dies ist das ägyptische pythagoreische Dreieck.

Die orangen Dreiecke haben das Seitenverhältnis 165:396:429 = 5:12:13. Dies ist das indische pythagoreische Dreieck.

Die magenta Dreiecke haben das Seitenverhältnis 165:280:325 = 33:56:65. Dies ist das schleswig-holsteinische pythagoreische Dreieck. Kontrolle: 33² + 56² = 1089 + 3136 = 4225 = 65².

Je zwei der außenliegenden Katheten ergeben eine Dreiecksseite. Die Dreiecksseiten sind daher ganzzahlig.

5 Neue Form der Problemstellung

Wir müssen drei Paare von pythagoreischen Dreiecken finden, deren Winkel beim Inkreismittelpunkt I „aufgehen“, sich also auf 360° addieren.

6 Pythagoreische Dreiecke

Die klassische Parametrisierung der pythagoreischen Dreiecke geht wie folgt. Zu teilerfremden ganzzahligen u > v > 0 mit ungleicher Parität sind a = u² – v², b = 2uv, c = u² + v² die Seiten eines pythagoreischen Dreieckes. Die Seiten sind teilerfremd. Weiter ist β = 2arctan(v/u). Beweis durch Nachrechnen (Additionstheorem für den Tangens).

In unserem Beispiel:

Für u₁ = 2 und v₁ = 1 ergibt sich a₁ = 3, b₁ = 4, c₁ = 5 (ägyptisches Dreieck). Es ist β₁ ≈ 53.130102354155979°.
Für u₂ = 3 und v₂ = 2 ergibt sich a₂ = 5, b₂ = 12, c₂ = 13 (indisches Dreieck). Es ist β₂ ≈ 67.380135051959574°.

Für u₃ = 7 und v₃ = 4 ergibt sich a₃ = 33, b₃ = 56, c₃ = 65. Es ist β₃ ≈ 59.489762593884447°.

Weiter ist 2(β₁ + β₂ + β₃) = 360°. Dies kann auch in der Form arctan(v₁/u₁) + arctan(v₂/u₂) + arctan(v₃/u₃) = π/2 geschrieben werden.

7 Konstruktionsweg

Wir benötigen zunächst drei Parameterpaare u₁, v₁, u₂, v₂, u₃, v₃ mit arctan(v₁/u₁) + arctan(v₂/u₂) + arctan(v₃/u₃) = π/2. Die zugehörigen pythagoreischen Dreiecke setzen wir an den Ecken mit den Winkeln β zusammen. Die von diesen Ecken ausgehenden Katheten bringen wir auf eine gemeinsame Länge, indem wir die Dreiecke auf das kleinste gemeinsame Vielfache der Katheten strecken. Dies ist der Inkreisradius.

Die Bedingung arctan(v₁/u₁) + arctan(v₂/u₂) + arctan(v₃/u₃) = π/2 formen wir um. Zunächst folgt aus dem Additionstheorem für den Tangens

tan(arctan(v₁/u₁) + arctan(v₂/u₂)) = (v₁u₂ + v₂u₁)/(u₁u₂ – v₁v₂)

also:

arctan(v₁/u₁) + arctan(v₂/u₂) = arctan((v₁u₂ + v₂u₁)/(u₁u₂ – v₁v₂))

Wegen

arctan(x) + arctan(1/x) = π/2

ist arctan(v₁/u₁) + arctan(v₂/u₂) + arctan((u₁u₂ – v₁v₂)/ (v₁u₂ + v₂u₁)) = π/2

Wir verfahren nun asymmetrisch, indem wir u₁, v₁, u₂, v₂ wählen und u₃, v₃ passend bestimmen, nämlich zunächst u₃ = v₁u₂ + v₂u₁ und v₃ = u₁u₂ – v₁v₂. Dann kürzen wir u₃ und v₃ mit dem größten gemeinsamen Teiler. Wenn nun u₃ > v₃ > 0, können wir diese Werte als Parameter für das dritte pythagoreische Dreieck verwenden. Andernfalls müssen wir u₁, v₁, u₂, v₂ neu wählen.

Schließlich müssen die pythagoreischen Dreiecke noch so gestreckt werden, dass die von den gemeinsamen Ecken ausgehenden Katheten gleich lang werden. Dies ist dann der Inkreisradius.

8 Einige Lösungen

Die Tabelle 1 gibt einige Lösungen. Die grün markierten Parameter sind gewählt, die restlichen Daten berechnet. Die Daten wiederholen sich in vertauschten Reihenfolgen.

u1	v1	u2	v2	u3	v3	a	b	c	r	AI	BI	CI
2	1	2	1	4	3	100	100	56	21	35	35	75
2	1	3	2	7	4	676	500	616	165	275	429	325
2	1	4	3	2	1	100	56	100	21	35	75	35
2	1	5	2	9	8	3364	3500	816	357	595	493	3045
2	1	5	4	13	6	6724	3000	6916	1197	1995	5453	1845
2	1	6	5	16	7	14884	5500	15456	2277	3795	12627	3355
3	2	2	1	7	4	500	676	616	165	429	275	325
3	2	3	2	12	5	2028	2028	2856	595	1547	1547	845
3	2	4	1	11	10	1156	1352	308	105	273	119	1105
3	2	4	3	17	6	37500	28392	51612	8855	23023	31625	11375
3	2	5	2	16	11	3364	4732	3168	945	2457	1305	2639
3	2	5	4	22	7	6724	4056	8932	1305	3393	5945	1599
3	2	6	5	27	8	44652	22308	57456	7315	19019	40565	8723
4	1	3	2	11	10	1352	1156	308	105	119	273	1105
4	1	4	3	16	13	25000	16184	12064	3045	3451	10875	14875
4	1	5	4	21	16	13448	6936	8288	1665	1887	7585	6273
4	1	6	5	26	19	29768	12716	20748	3465	3927	19215	11407
4	3	2	1	2	1	56	100	100	21	75	35	35
4	3	3	2	17	6	28392	37500	51612	8855	31625	23023	11375
4	3	4	1	16	13	16184	25000	12064	3045	10875	3451	14875
4	3	4	3	24	7	15000	15000	25296	3689	13175	13175	4375
4	3	5	2	23	14	6728	12500	10212	2331	8325	3219	5075
4	3	5	4	31	8	94136	75000	148304	18837	67275	85813	21525
4	3	6	1	22	21	32856	37500	5676	1505	5375	1591	32375
4	3	6	5	38	9	625128	412500	932292	104951	374825	582001	117425
5	2	2	1	9	8	3500	3364	816	357	493	595	3045
5	2	3	2	16	11	4732	3364	3168	945	1305	2457	2639
5	2	4	3	23	14	12500	6728	10212	2331	3219	8325	5075
5	2	5	4	30	17	235340	100920	207740	38493	53157	175357	74907
5	2	6	5	37	20	520940	185020	478040	74613	103037	413763	136213
5	4	2	1	13	6	3000	6724	6916	1197	5453	1995	1845
5	4	3	2	22	7	4056	6724	8932	1305	5945	3393	1599
5	4	4	1	21	16	6936	13448	8288	1665	7585	1887	6273
5	4	4	3	31	8	75000	94136	148304	18837	85813	67275	21525
5	4	5	2	30	17	100920	235340	207740	38493	175357	53157	74907
5	4	5	4	40	9	67240	67240	121520	13671	62279	62279	15129
5	4	6	1	29	26	32856	47068	16588	3465	15785	3663	31857
5	4	6	5	49	10	446520	369820	751660	75933	345917	421083	82533
6	1	4	3	22	21	37500	32856	5676	1505	1591	5375	32375
6	1	5	4	29	26	47068	32856	16588	3465	3663	15785	31857
6	1	6	5	36	31	312564	180708	149544	25795	27269	143045	173789
6	5	2	1	16	7	5500	14884	15456	2277	12627	3795	3355
6	5	3	2	27	8	22308	44652	57456	7315	40565	19019	8723
6	5	4	1	26	19	12716	29768	20748	3465	19215	3927	11407
6	5	4	3	38	9	412500	625128	932292	104951	582001	374825	117425
6	5	5	2	37	20	185020	520940	478040	74613	413763	103037	136213
6	5	5	4	49	10	369820	446520	751660	75933	421083	345917	82533
6	5	6	1	36	31	180708	312564	149544	25795	143045	27269	173789
6	5	6	5	60	11	223260	223260	417480	38269	212219	212219	40931

Tab. 1: Einige Lösungen

Die Zahlen sind recht groß und lassen sich nicht visualisieren.

9 Ganzzahlige Höhen

Der Umfang und der Inkreisradius der Dreiecke sind ganzzahlig, daher ist der Flächeninhalt ganzzahlig oder halbzahlig. Die Seitenlängen sind ganzzahlig. Somit sind die zugehörigen Dreieckshöhen rational. Durch Strecken der Dreiecke mit dem kleinsten gemeinsamen Vielfachen aller vorkommenden Nenner können die Höhen ganzzahlig dargestellt werden. Die übrigen Daten bleiben dabei ganzzahlig.

10 Verallgemeinerung

Problemstellung und Verfahren können verallgemeinert werden wie folgt. Gesucht ist ein Tangenten-n-Eck mit ganzzahligen Seitenlängen, ganzzahligem Inkreisradius und ganzzahligen Abschnitten von den Ecken zum Mittelpunkt des Inkreises.

Wir besprechen exemplarisch ein Tangentenviereck. Zunächst wählen wir drei Parameterpaare u₁, v₁, u₂, v₂, u₃, v₃. Aus dem Additionstheorem für den Tangens folgt:

arctan(v₁/u₁) + arctan(v₂/u₂) + arctan(v₃/u₃) = arctan((v₁u₂u₃ + u₁v₂u₃ + u₁u₂v₃ – v₁v₂v₃)/(u₁u₂u₃ – v₁v₂u₃ – v₁u₂v₃ – u₁v₂v₃))

Wir definieren nun

u₄ = v₁u₂u₃ + u₁v₂u₃ + u₁u₂v₃ – v₁v₂v₃

v₄ = u₁u₂u₃ – v₁v₂u₃ – v₁u₂v₃ – u₁v₂v₃

und kürzen mit allfälligen gemeinsamen Teilern. Sofern u₄ > v₄ > 0 (andernfalls müssen wir die drei Parameterpaare u₁, v₁, u₂, v₂, u₃, v₃ neu wählen) ergibt sich:

arctan(v₁/u₁) + arctan(v₂/u₂) + arctan(v₃/u₃) + arctan(v₄/u₄) = π/2

Wir können nun vier Paare von spiegelbildlichen pythagoreischen Dreiecken nach geeignetem Strecken auf den Inkreisradius zu einem ganzzahligen Tangentenviereck zusammensetzen.

Beispiel: Mit u₁ = 2, v₁ = 1, u₂ = 3, v₂ = 2, u₃ = 4, v₃ = 1 ergibt sich u₄ = 32, v₄ = 9.

Für das zugehörige Tangentenviereck (Abb. 3) gilt: AI = 23575, BI = 36777, CI = 16031, DI = 16575, r = 14145, a = 52808, b = 41492, c = 16184, d = 27500.

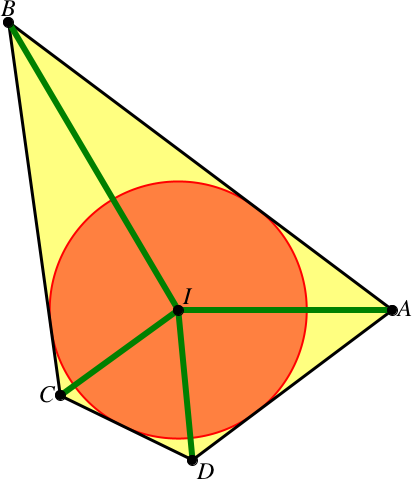
Abb. 3: Ganzzahliges Tangentenviereck

Weblinks

Hans Walser: Inkreismittelpunktabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/I/Inkreismittelpunktabschnitte/Inkreismittelpunktabschnitte.html

Hans Walser: Tangentenviereck

http://www.walser-h-m.ch/hans/Miniaturen/T/Tangentenviereck/Tangentenviereck.html