1 Worum geht es?

Im dreidimensionalen Raum sind zwei Geraden in der Regel windschief. Sie haben keinen Schnittpunkt und sind nicht parallel (Abb. 1).

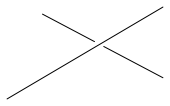
Abb. 1: Windschiefe Geraden

Die Frage ist, ob es in höheren Dimensionen auch zum Beispiel windschiefe Ebenen gibt.

Die Frage wird exemplarisch angegangen.

2 Bezeichnungen

Im n-dimensionalen Raum bezeichnen wir mit

den Vektor, der an der k-ten Stelle eine 1 und sonst ausschließlich Nullen hat. Also zum Beispiel im 5-dimensionalen Raum:

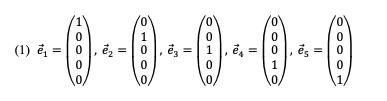
Mit r₁, r₂, … bezeichnen wir reelle Parameter.

3 Beispiel im Raum

Im dreidimensionalen Raum wählen wir die beiden Geraden g₁ und g₂ wie folgt:

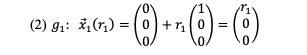
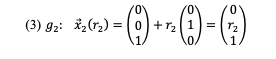
Für den Abstand eines beliebigen Punktes A₁auf g₁ zu einem beliebigen Punkt A₂ auf g₂ erhalten wir:

Die beiden Geraden haben also keinen gemeinsamen Punkt. Da sie linear unabhängige Richtungsvektoren haben, sind sie auch nicht parallel. Sie sind also windschief.

In (4) erhalten wir die Gleichheit genau für r₁ = r₂ = 0. Die zugehörigen Geradenpunkte (0,0,0) und (1,0,0) definieren die Minimaltransversale. Sie steht senkrecht auf den beiden Geraden g₁ und g₂.

Die Abbildung 2 zeigt die Situation in isometrischer Normalaxonometrie. Es sind Ausschnitte von g₁ und g₂ sowie die Minimaltransversale m eingezeichnet. Die Konstruktion orientiert sich am Einheitswürfel.

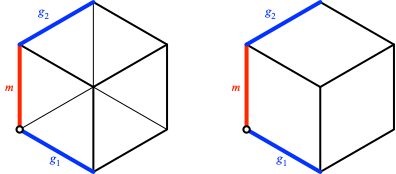
Abb. 2: Windschiefe Geraden

4 Beispiel im vierdimensionalen Raum

Im vierdimensionalen Raum wählen wir eine Gerade g₁ und eine Ebene g₂ wie folgt:

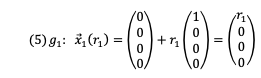
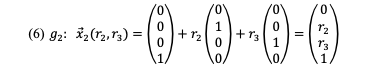
Für den Abstand eines beliebigen Punktes A₁auf g₁ zu einem beliebigen Punkt A₂ auf g₂ erhalten wir:

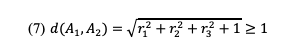
Die Gerade und die Ebene haben also keinen gemeinsamen Punkt. Da sie linear unabhängige Richtungsvektoren haben, sind sie auch nicht parallel. Wir haben also eine Gerade und dazu eine windschiefe Ebene. Die Gerade steht senkrecht auf der Ebene, ohne sie zu schneiden.

Die Abbildung 3 zeigt die Situation in isometrischer ebener Normalaxonometrie. Es sind Ausschnitte von g₁ und g₂ sowie die Minimaltransversale m eingezeichnet. Die Zeichnung orientiert sich am vierdimensionalen Hyperwürfel.

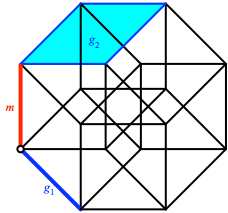
Abb. 3: Windschiefe Geraden

5 Beispiele im fünfdimensionalen Raum

5.1 Gerade und dreidimensionaler Unterraum

Im fünfdimensionalen Raum wählen wir die eine Gerade g₁ und einen dreidimensionalen Unterraum g₂ wie folgt:

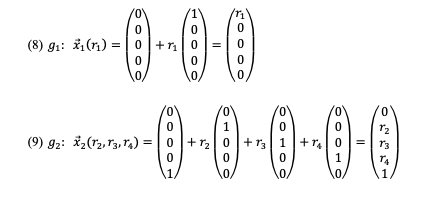
Für den Abstand eines beliebigen Punktes A₁auf g₁ zu einem beliebigen Punkt A₂ auf g₂ erhalten wir:

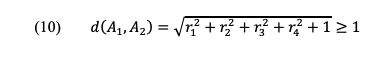
Die Gerade und der dreidimensionale Unterraum haben also keinen gemeinsamen Punkt. Da sie linear unabhängige Richtungsvektoren haben, sind sie auch nicht parallel. Sie sind also windschief zueinander. Die Gerade steht senkrecht auf dem dreidimensionalen Unterraum, ohne diesen zu schneiden.

Die Abbildung 4 zeigt die Situation in isometrischer Normalaxonometrie. Es sind Ausschnitte von g₁ und g₂ sowie die Minimaltransversale m eingezeichnet.

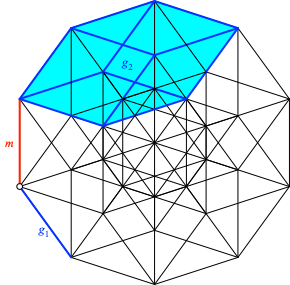
Abb. 4: Gerade und windschiefer dreidimensionaler Unterraum

5.2 Zwei Ebenen

Im fünfdimensionalen Raum wählen wir zwei Ebenen g₁ und g₂ wie folgt:

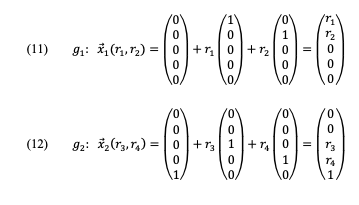
Für den Abstand eines beliebigen Punktes A₁auf g₁ zu einem beliebigen Punkt A₂ auf g₂ erhalten wir:

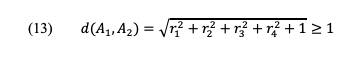
Die beiden Ebenen haben also keinen gemeinsamen Punkt. Da sie linear unabhängige Richtungsvektoren haben, sind sie auch nicht parallel. Sie sind also windschief zueinander. Die beiden Ebenen stehen senkrecht zueinander.

Die Abbildung 5 zeigt die Situation in isometrischer Normalaxonometrie. Es sind Ausschnitte von g₁ und g₂ sowie die Minimaltransversale m eingezeichnet.

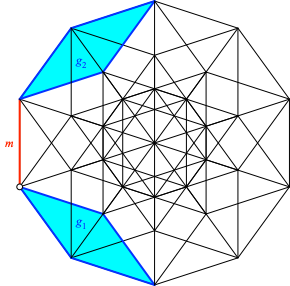
Abb. 5: Zwei windschiefe Ebenen

6 Allgemein

Wir sehen, wie der Hase läuft.

Im n-dimensionalen Raum können wir zu i und j mit i + j ≤ n – 1 einen i-dimensionalen und einen j-dimensionalen Unterraum konstruieren, die keinen Schnittpunkt haben und auch nicht parallel sind. Nach unserer Konstruktion sind sie aber orthogonal.

Die beiden Unterräume sind windschief.

Im dreidimensionalen Anschauungsraum funktioniert das nur mit zwei Geraden.