Hans Walser, [20150821]
Visualizations of the Fibonacci recursion
Figure 1 depicts a classical visualization.
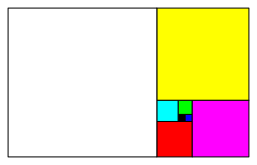
Fig. 1: Classical
We have a spiral arrangement without overlapping squares.
In this figure and also in the following we use a color code according to table 1.
|
No |
RGB |
Color |
Example |
New No |
Fibonacci |
|
0 |
0,0,0 |
Black |
|
1 |
1 |
|
1 |
0,0,1 |
Blue |
|
2 |
1 |
|
2 |
0,1,0 |
Green |
|
3 |
2 |
|
3 |
0,1,1 |
Cyan |
|
4 |
3 |
|
4 |
1,0,0 |
Red |
|
5 |
5 |
|
5 |
1,0,1 |
Magenta |
|
6 |
8 |
|
6 |
1,1,0 |
Yellow |
|
7 |
13 |
|
7 |
1,1,1 |
White |
|
8 |
21 |
Tab. 1: Color code
In figure 2 we have a linear arrangement.
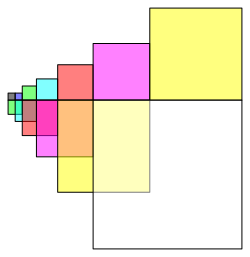
Fig. 2: Linear arrangement
This can be done also with other polygons. The figure 3 gives a version with regular triangles.
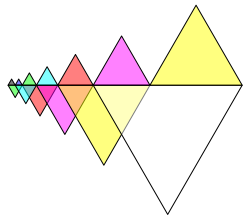
Fig. 3: Regular triangles
The figure 4 works with regular pentagons.
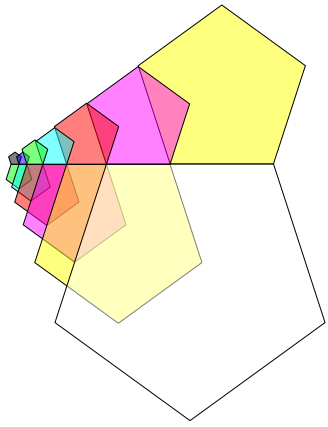
Fig. 4: Regular pentagons
The ŇrooflineÓ is not straightforward, but interrupted.
Taking a geometric sequence based on the golden section
![]()
leads to a proper roofline (Fig. 5). But this is no more a Fibonacci sequence. The difference is visible at the beginning.
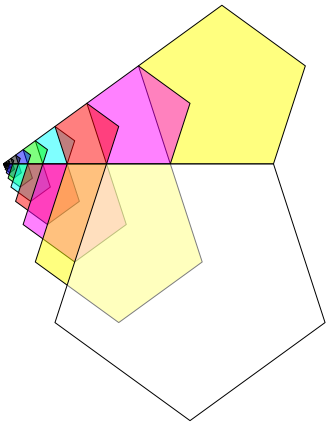
Fig. 5: Golden section
Parts of this figure can be used to draw a regular pentagon (Fig. 6).
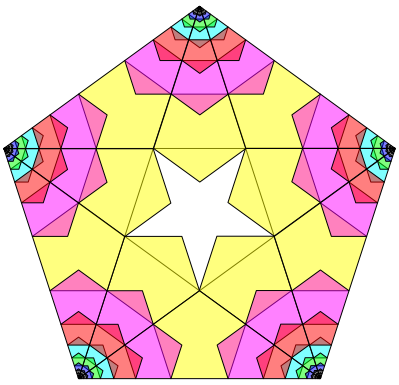
Fig. 6: Pentagon
In the following figures we will work again with the Fibonacci sequence.
The figure 7 uses half hexagons.
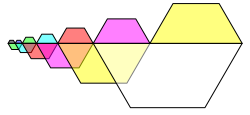
Fig. 7: Half hexagons
In figure 8 half circles.
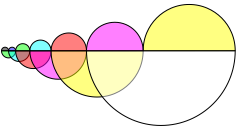
Fig. 8: Half circles
In figure 9 half circles again, but this time with a golden geometric sequence.
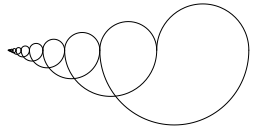
Fig. 9: Golden section