Hans Walser, [20240205]

Verschränkung

Anregung: Zvonimir Durcevic, Wien

1 Worum es geht

Arithmetische Spielerei mit Summen. Binomialkoeffizienten

2 Beispiele

Wir rechnen:

1•1 = 1

1•2 + 2•1 = 4

1•3 + 2•2 + 3•1 = 10

1•4 + 2•3 + 3•2 + 4•1 = 20

1•5 + 2•4 + 3•3 + 4•2 + 5•1 = 35

Wie geht es weiter?

Formal: Wir berechnen

s(n) = sum(k*(n + 1 – k), k = 1 .. n)

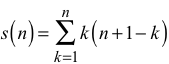
3 Einmaleins

Die Abbildung 0 zeigt das «kleine Einmaleins», also die Multiplikationstabelle.

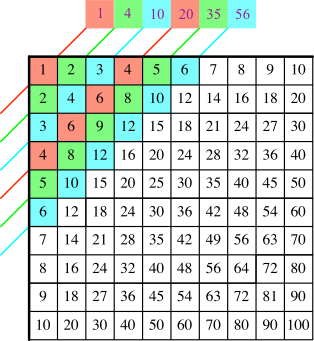
Abb. 0: Einmaleins. Schrägzeilensummen

Wir addieren die Zahlen in den markierten Schrägzeilen und erhalten ebenfalls die Summen 1, 4, 10, 20, 35, 56.

4 Binomialkoeffizienten

Die Abbildung 1 zeigt das Pascal-Dreieck der Binomialkoeffizienten. Wir erkennen unsere Zahlen in der Schrägzeile binomial(m, 3).

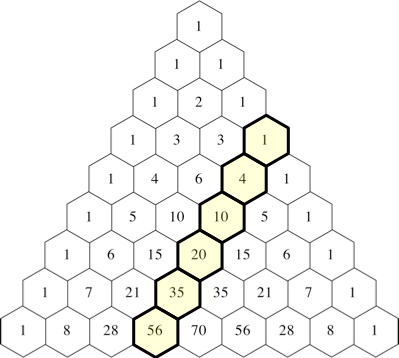
Abb. 1: Binomialkoeffizienten

5 Vermutung

s(n) = binomial(n + 2, 3)

6 Visualisierung

Wir visualisieren den Fall n = 5, also:

1•5 + 2•4 + 3•3 + 4•2 + 5•1 = 35

Die Abbildung 2 zeigt die Summanden einzeln mit Würfeln dargestellt.

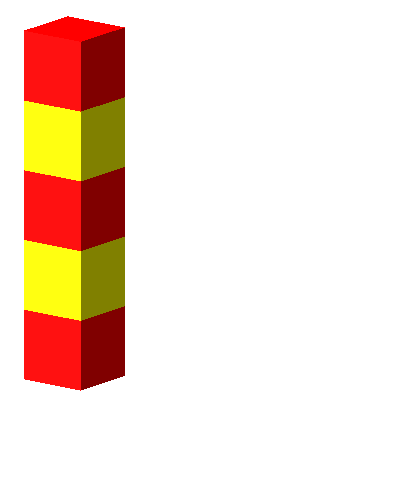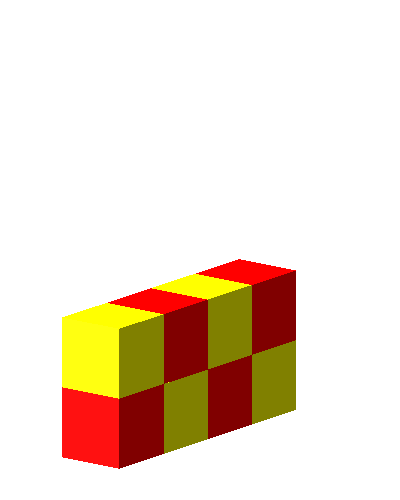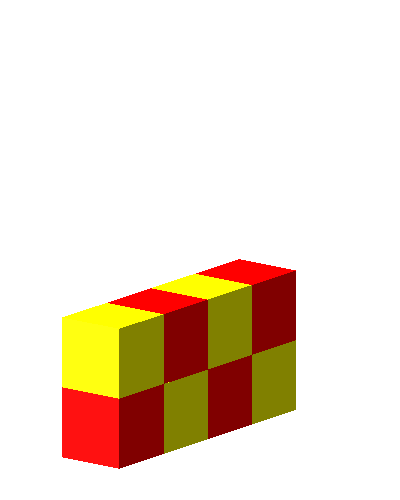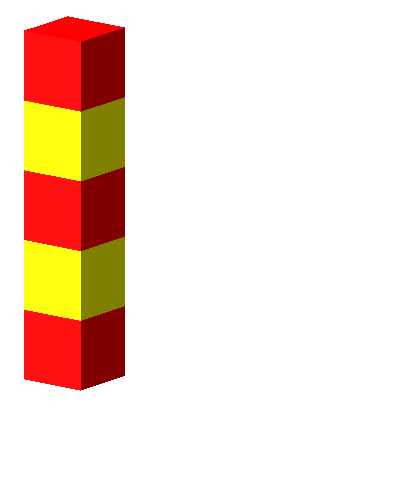
Abb. 2: Summanden

In der Abbildung 3 wird aufsummiert.

Abb. 3: Aufsummieren

Die Abbildungen 4 und 5 zeigen die Summe.

Abb. 4: Summe

Abb. 5: Summe von allen Seiten

Die Abbildung 6 zeigt dasselbe Spielchen für n = 10. Auf den Seiten erkennen wir ein Schachbrettmuster sowie waagerechte und senkrechte Streifen.

Abb. 6: n = 10

7 Induktionsbeweis

7.1 Veranderung

Die Vermutung

s(n) = binomial(n + 2, 3)

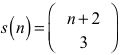
stimmt für n = 1 .. 5, das haben wir ja nachgerechnet.

7.2 Induktionsschritt

Die Abbildung 7 zeigt nun, wie wir von n = 5 auf n = 6 kommen.

Wir müssen eine Treppe der Höhe 6 anfügen. Die Treppe besteht aus 1 + 2 + 3 + 4 + 5 + 6 = 21 Würfeln. Nun ist aber 1 + 2 + 3 + 4 + 5 + 6 = 1/2•6•(1 + 6).

Abb. 7: Induktionsschritt

Für den Induktionsschritt von n auf n + 1 müssen wir eine Treppe mit 1 + 2 + … + (n + 1) = 1/2•(n + 1) •(n + 2) Würfeln anfügen. Nun ist aber:

1/2•(n + 1) •(n + 2) = binomial(n + 2, 2)

Somit erhalten wir:

s(n + 1) = s(n) + binomial(n + 2, 2) = binomial(n + 2, 3) + binomial(n + 2, 2) = binomial(n + 2, 2) + binomial(n + 2, 3)

Wegen der Rekursionsformel der Binomialkoeffizienten

binomial(n + 1 , k) = binomial(n , k – 1) + binomial(n , k)

ist aber:

binomial(n + 2, 2) + binomial(n + 2, 3) = binomial(n + 3, 3)

Damit ist unsere Vermutung bewiesen.

8 Rechnerisches Vorgehen

Wir bilden die Differenz s(6) – s(5):

s(6) = 1•6 + 2•5 + 3•4 + 4•3 + 5•2 + 6•1

– s(5) = – 1•5 – 2•4 – 3•3 – 4•2 – 5•1
–––– –––––––––––––––––––––––––––
6 + 5 + 4 + 3 + 2 + 1

Wir sehen wie die Treppe entsteht.