Hans Walser, [20240423]

Überlagerung

Anregung: Hans Humenberger, Uni Wien

1 Worum es geht

Spielerei im Dreieck. Optimierung. Überlagerung. Zerlegungen. Trickfilm

2 Optimale Rechtecke im Dreieck

Einem spitzwinkligen Dreieck kann auf drei Arten ein Rechteck mit maximalem Flächeninhalt einbeschrieben werden (Abb. 1). Jedes Rechteck hat zwei Ecken auf einer Dreieckseite und die beiden anderen je im Mittelpunkt der beiden anderen Dreieckseiten.

Abb. 1.1: Optimales Rechteck

Abb. 1.2: Optimales Rechteck

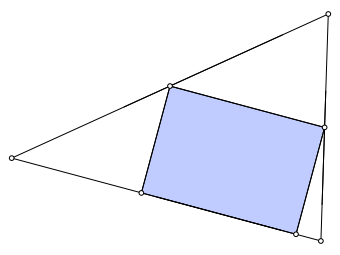
Abb. 1.3: Optimales Rechteck

Welchen Flächenanteil des Dreiecks belegen die optimalen Rechtecke?

3 Überlagerung

Die Abbildung 2 zeigt die Überlagerung der drei Rechtecke.

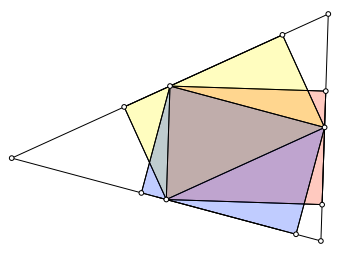
Abb. 2: Überlagerung

Welche Flächenanteile des Dreiecks sind gar nicht bedeckt, einfach bedeckt, doppelt bedeckt oder dreifach bedeckt?

4 Zerlegung

Zur Bearbeitung der oben gestellten Fragen zerlegen wir das Dreieck gemäß Abbildung 3. Die Zerlegung geht so: Zunächst wird durch die Verbindungen der Kantenmitten das Dreieck in vier kongruente Dreiecke zerlegt. Jedes dieser Dreiecke zerlegen wir mit seinen Höhen in sechs Teildreiecke. Wir haben also sechsmal vier Teildreiecke. Die jeweils vier kongruenten Teildreiecke tragen dieselbe Farbe. Farben: rot, grün, blau, himmelblau, magenta, gelb.

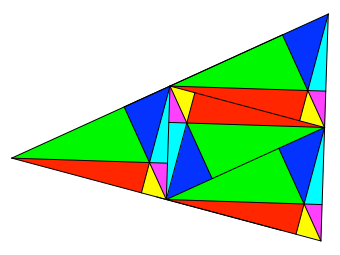
Abb. 3: Zerlegung

Diese Zerlegung kann auch durch Falten erreicht werden (Abb. 4). Für den Faltprozess wird aus didaktischen Gründen angenommen, das Papierdreieck sei auf der Vorderseite gelb und auf der Rückseite himmelblau.

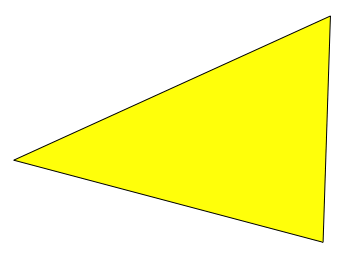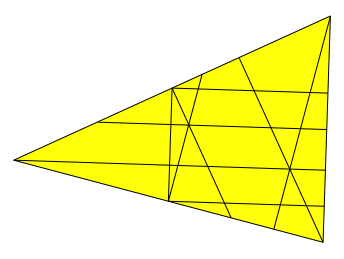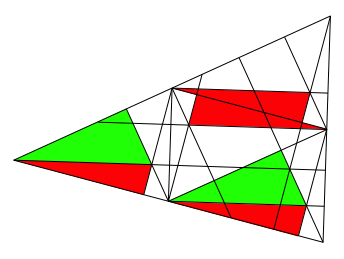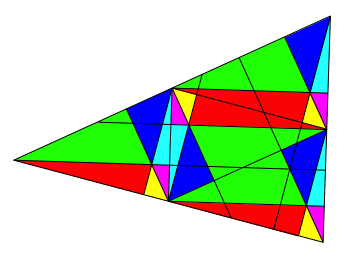
Abb. 4: Falten und Färben

Die Abbildung 5 zeigt das Ergebnis dieses Falt- und Färbe-Prozesses.

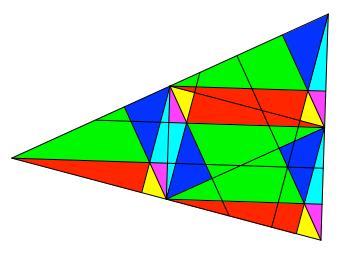
Abb. 5: Mit Falten und Färben

Ein Vergleich mit der Zerlegung der Abbildung 3 zeigt, dass einige Faltlinien zu lang sind. Dies liegt am Faltprozess, eine Faltlinie geht immer übers ganze Papier. Dasselbe Problem haben wir ja auch beim Zerlegen einer Platte (zum Beispiel Spanplatte) mit einer Kreissäge. Wegen der Plattendicke ist es nicht möglich, an einem bestimmten Punkt den Schnitt zu beenden. Das Problem ist aber mit einer Bandsäge oder einer Stichsäge lösbar, oder wie in der guten alten Zeit mit einer Zimmermannssäge oder einem Fuchsschwanz.

5 Optimale Rechtecke

In jedem optimalen Rechtecke kommt jede Farbe genau zweimal vor (Abb. 6). Die Rechtecke belegen also je die Hälfte der Dreiecksfläche.

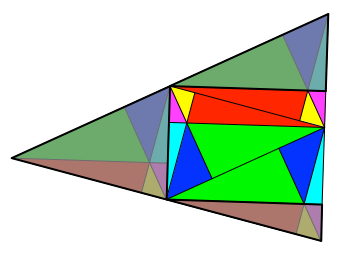
Abb. 6.1: Optimales Rechteck

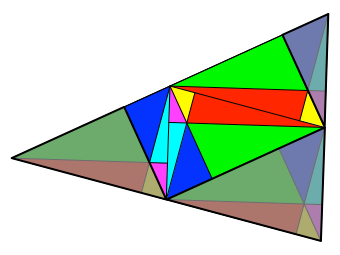
Abb. 6.2: Optimales Rechteck

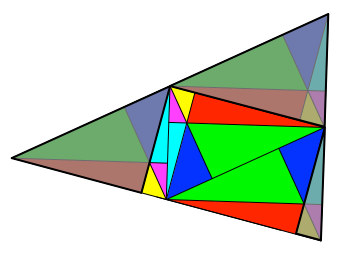
Abb. 6.3: Optimales Rechteck

6 Überlagerungen

Der durch die optimalen Rechtecke freigelassene Bereich ist in der Abbildung 7.0 dargestellt. Der Rest ist abgedunkelt. Im nicht abgedunkelten Teil kommt jede Farbe genau einmal vor. Der nicht bedeckte Anteil macht also einen Viertel der Dreiecksfläche aus.

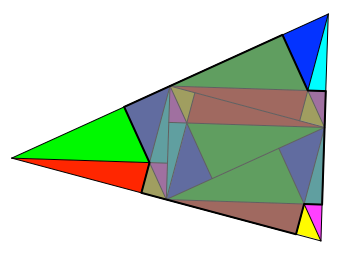
Abb. 7.0: Nicht bedeckter Teil

Die Abbildung 7.1 zeigt den einfach bedeckten Teil. Auch dieser macht einen Viertel der Dreiecksfläche aus.

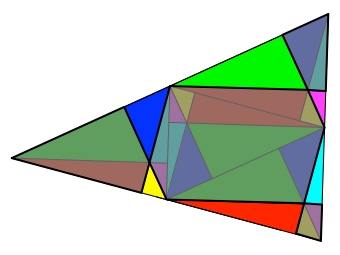
Abb. 7.1: Einfach bedeckter Teil

Auch der doppelt bedeckte Teil (Abb. 7.2) macht einen Viertel der Dreiecksfläche aus.

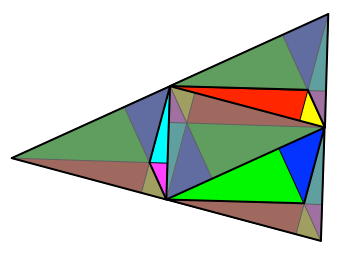
Abb. 7.2: Doppelt bedeckter Teil

Dreifach bedeckt ist das Kantenmittendreieck (Abb. 7.3). Dieses macht ebenfalls einen Viertel der Dreiecksfläche aus.

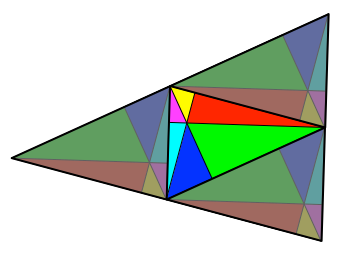
Abb. 7.3: Dreifach bedeckter Teil

7 Das Feuerbach-Sechseck

Das Feuerbach-Sechseck (Abb. 8) besteht aus den mindestens zweifach bedeckten Teilen der Abbildung 2. Im Feuerbach-Sechseck kommt jede Farbe zweimal vor, wie bei den optimalen Rechtecken. Der Flächenanteil des Feuerbach-Sechseckes ist somit die Hälfte der Dreiecksfläche.

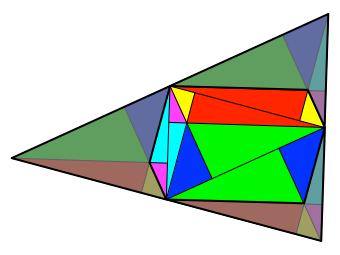
Abb. 8: Feuerbach-Sechseck

Das Feuerbach-Sechseck ist ein punktsymmetrisches Sehnensechseck (Abb. 9). Sein Umkreis ist der Feuerbach-Kreis. Daher der Name Feuerbach-Sechseck.

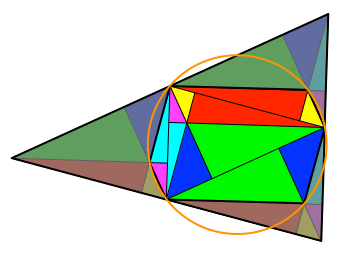
Abb. 9: Feuerbach-Kreis

Im Feuerbach-Sechseck kann das Bild eines Quaders erkannt werden (Abb. 10). Jede der drei sichtbaren Seiten des Quaders besteht aus zweimal zwei Farben.

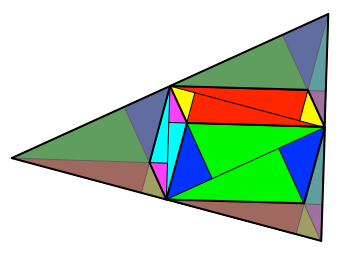
Abb. 10: Bild eines Quaders

Literatur

Hans Humenberger: Paper Folding and Reasoning. To appear in: Mathematics in School, Mathematical Association, UK