1 Worum geht es?

Verallgemeinerung eines Problems der Dreiecksgeometrie.

2 In der Ebene

2.1 Problemstellung

Hans Schupp stellte die Aufgabe: Es wird mit drei Würfeln gewürfelt. Die Augen geben Längen von Strecken vor. Mit welcher Wahrscheinlichkeit lässt sich daraus ein Dreieck konstruieren?

2.2 Verallgemeinerung

Wir verallgemeinern die Aufgabe, indem wir mit Zufallsgeneratoren arbeiten, welche die natürlichen Zahlen von 1 bis N mit gleicher Wahrscheinlichkeit liefern.

2.3 Bearbeitung

Wir arbeiten mit brute force mit folgendem Programm (Abb. 1 für N = 6):

Ein Bild, das Text enthält.

Automatisch generierte Beschreibung

Abb. 1: Programm

Die Tabelle 1 gibt die ersten Werte bezüglich N.

N	Anzahl	N³	Relative Häufigkeit	Relative Häufigkeit
1	1	1	1	1
2	5	8	5/8	0.6250000000
3	15	27	5/9	0.5555555556
4	34	64	17/32	0.5312500000
5	65	125	13/25	0.5200000000
6	111	216	37/72	0.5138888889
7	175	343	25/49	0.5102040816
8	260	512	65/128	0.5078125000
9	369	729	41/81	0.5061728395
10	505	1000	101/200	0.5050000000
11	671	1331	61/121	0.5041322314
12	870	1728	145/288	0.5034722222
13	1105	2197	85/169	0.5029585799
14	1379	2744	197/392	0.5025510204
15	1695	3375	113/225	0.5022222222
16	2056	4096	257/512	0.5019531250
17	2465	4913	145/289	0.5017301038
18	2925	5832	325/648	0.5015432099
19	3439	6859	181/361	0.5013850416
20	4010	8000	401/800	0.5012500000
21	4641	9261	221/441	0.5011337868
22	5335	10648	485/968	0.5010330579
23	6095	12167	265/529	0.5009451796
24	6924	13824	577/1152	0.5008680556
25	7825	15625	313/625	0.5008000000
26	8801	17576	677/1352	0.5007396450
27	9855	19683	365/729	0.5006858711
28	10990	21952	785/1568	0.5006377551
29	12209	24389	421/841	0.5005945303
30	13515	27000	901/1800	0.5005555556

Tab. 1: Werte

2.4 Formel

Die Formel geht so (Beweis fehlt):

Relative Häufigkeit = (1 + 1/N^2)/2

Der Grenzwert für wachsendes N ist ½.

2.5 Visualisierung

Wenn für ein Tripel [a, b, c] die Dreiecksungleichung erfüllt ist, zeichnen wir ein achsenparalleles Würfelchen mit den diametralen Ecken [a – 1, b – 1, c – 1] und [a, b, c]. Die Abbildung 2 zeigt die Situation für N = 6. Die Figur besteht aus einem regelmäßigen Tetraeder, welches einem 6×6×6-Würfel einbeschrieben ist, sowie aus einem unregelmäßigen Tetraeder mit drei paarweise orthogonalen Kanten, welches einen Zwischenraum zwischen dem regelmäßigen Tetraeder und einer Würfelecke ausfüllt.

Abb. 2: Visualisierung

Für wachsendes N nähert sich das Volumen des regelmäßigen Tetraeders einem Drittel des Würfelvolumens und das Volumen des Eckentetraeders einem Sechstel des Würfelvolumens. Die Grenzfigur ist also volumenmäßig halb so groß wie der Würfel. Damit ist der Grenzwert ½ gezeigt. Wir haben hier eine räumliche Visualisierung eines zweidimensionalen Problems.

3 Verallgemeinerung: Tetraeder

Es wird mit sechs Zufallsgeneratoren gearbeitet. Die Ergebnisse geben Längen von sechs Strecken a, b, c, d, e, f vor. Mit welcher Wahrscheinlichkeit lässt sich daraus ein (allenfalls unregelmäßiges) Tetraeder gemäß Abbildung 3 bauen? — Die Anordnung der Kanten ist also vorgegeben und kann nicht permutiert werden.

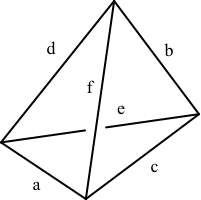
Abb. 3: Anordnung der Tetraederkanten

Es müssen folgende Ungleichungen erfüllt sein:

a+c>e and c+e>a and e+a>c

and c+b>f and b+f>c and f+c>b

and b+d>e and d+e>b and e+b>d

and a+d>f and d+f>a and f+a>d

Das Programm wird entsprechend länger (Abb. 4 für N = 4):

Abb. 4: Programm

Die Tabelle 2 gibt die ersten Werte in Abhängigkeit von N.

N	Anzahl	N⁶	Relative Häufigkeit	Relative Häufigkeit
1	1	1	1	1
2	15	64	15/64	0.2343750000
3	127	729	127/729	0.1742112483
4	648	4096	81/512	0.1582031250
5	2371	15625	2371/15625	0.1517440000
6	6927	46656	2309/15552	0.1484696502
7	17245	117649	17245/117649	0.1465800814
8	38112	262144	1191/8192	0.1453857422
9	76837	531441	76837/531441	0.1445823713
10	144015	1000000	28803/200000	0.1440150000

Tab. 2: Erste Werte

Ich habe weder eine schöne Formel noch einen Grenzwert für große N gefunden.

Für eine Visualisierung müssten wir im 6-dimensionalen Raum arbeiten.

Bei Permutation der Tetraederkanten kann es weitere Lösungen geben.