Hans Walser, [20220703]
Tetraeder in Halbkugel
1 Worum geht es?
Analogie eines ebenen Problems im Raum. Datenaufnahme.
2 In der Ebene
Das rechtwinklig gleichschenklige Dreieck ist das flächenmäßige größte Dreieck, das einem Halbkreis einbeschrieben werden kann (Abb. 1).
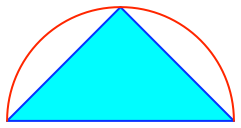
Abb. 1: Größtes Dreieck im Halbkreis
Begründung: Bei jedem anderen Dreieck sind sowohl Grundlinie wie auch zugehörige Höhe kleiner.
Bei einem Radius r = 1 ist die Dreiecksfläche ebenfalls 1.
Der Halbkreis wird manchmal als Thaleskreis bezeichnet.
3 Problemstellung
Analogie im Raum: Welches ist das größte Tetraeder, das einer Halbkugel einbeschrieben werden kann?
Für die Daten setzen wir den Halbkugelradius 1.
4 Die Lösung
Die Abbildung 2 zeigt das Tetraeder in einer schrägen Ansicht.
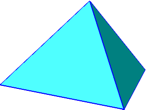
Abb. 2: Das Tetraeder
Die Abbildung 3 zeigt das Tetraeder von oben (Grundriss), von vorne (Aufriss) und von der Seite (Seitenriss) in der klassischen Anordnung.

Abb. 3: Risse
5 In der Halbkugel
Die Abbildungen 4 und 5 zeigen das Tetraeder in der Halbkugel.
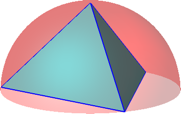
Abb. 4: Tetraeder in der Halbkugel
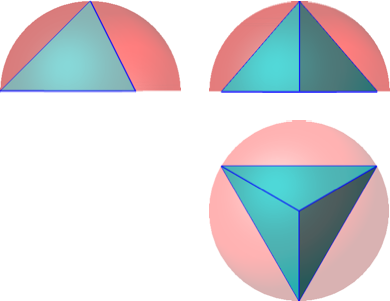
Abb. 5: Risse
6 Beschreibung
6.1 Längen
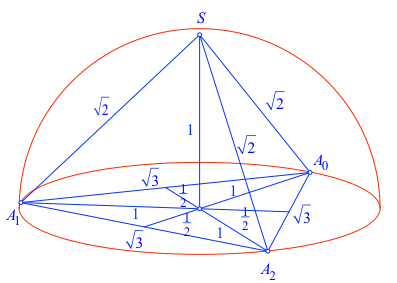
Abb. 6: Längen
Die Eckpunkte haben die Koordinaten:
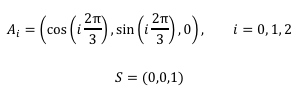
Das Bodendreieck A0A1A2 ist gleichseitig und hat die Höhe 3/2.
Die Abbildung 7 zeigt die Höhen der gleichschenkligen Seitendreiecke.
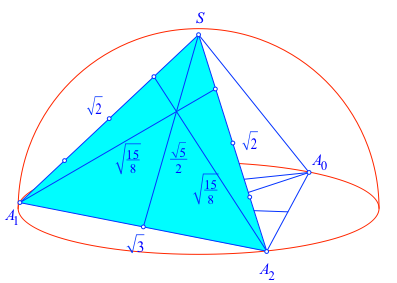
Abb. 7: Höhen der Seitendreiecke
6.2 Winkel
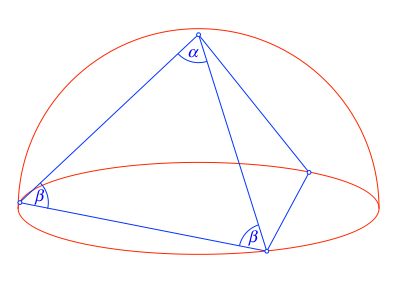
Abb. 8: Winkel der Seitendreiecke

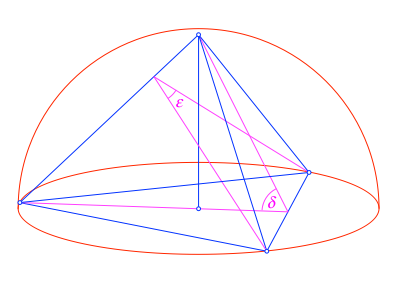
Abb. 9: Diederwinkel
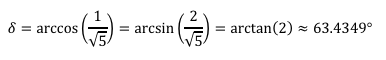
Dieser Winkel ist gleich dem Diagonalenschnittwinkel im goldenen Rechteck.
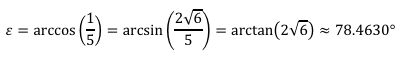
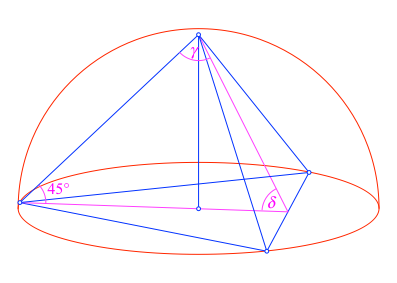
Abb. 10: Weitere Winkel
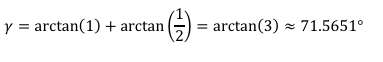
Diese letzte Beziehung kann leicht im Quadratraster eingesehen werden (Abb. 11).

Abb.
11: Proof without words
Literatur
Alsina, Claudi
& Nelsen, Roger B. (2013): Bezaubernde Beweise: eine Reise durch
die Eleganz der Mathematik. Berlin: Springer Spektrum.
Nelsen,
Roger B. (2000): Proofs without Words. MAA, The Mathematical Association of
America. ISBN 978-0883857007