1 Worum es geht

Tangentenviereck im Kontext der Kegelschnitte

2 Beginn mit Tangentenviereck

Wir beginnen mit einem Tangentenviereck gemäß Abbildung 1.

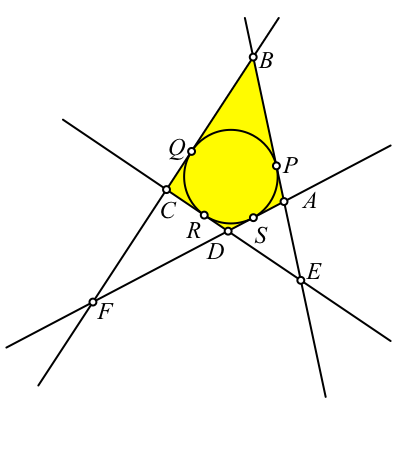
Abb. 1: Tangentenviereck

Auf Grund gleich langer Tangentenabschnitte gilt:

AE + AF = PE – PA + FS + AS = PE – PA + FS + PA = PE + FS

CF + CE = QF – QC + CR + RE = QF – QC + QC + RE = QF + RE = FS + PE

Somit ist AE + AF = CF + CE. Die Punkte A und C liegen also auf derselben Ellipse mit den Brennpunkten E und F (Abb. 2).

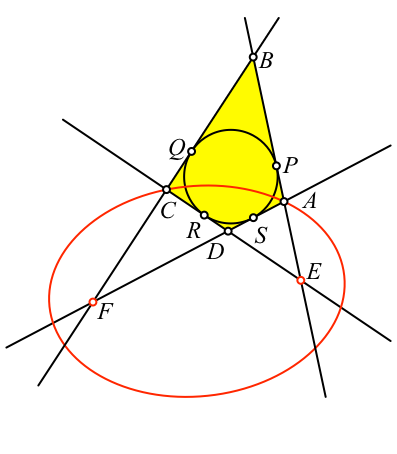
Abb. 2: Zwei Punkte auf einer Ellipse

Analog kann gezeigt werden, dass die Punkte B und D auf derselben Hyperbel mit ebenfalls den Brennpunkten E und F liegen (Abb. 3).

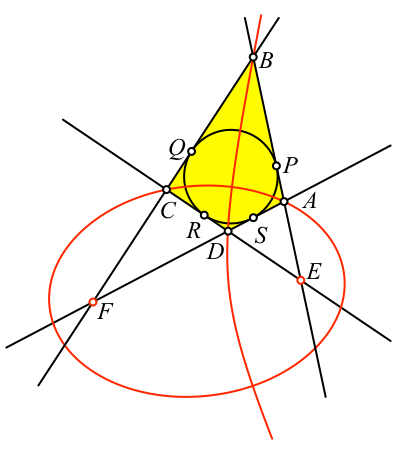
Abb. 3: Die zwei anderen Punkte auf einer Hyperbel

3 Umkehrung

Auf einer Ellipse mit den Brennpunkten E und F wählen wir zwei Punkte A uns C (Abb. 4). Weiter zeichnen wir die vier Geraden EA, EC, FA, FC.

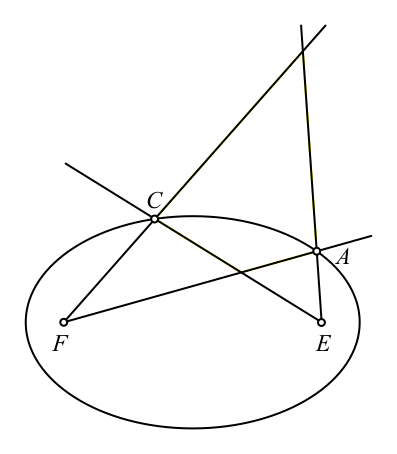
Abb. 4: Zwei Punkte auf der Ellipse

So entsteht ein Viereck, von dem wir zeigen möchten, dass es ein Tangentenviereck ist (Abb. 5).

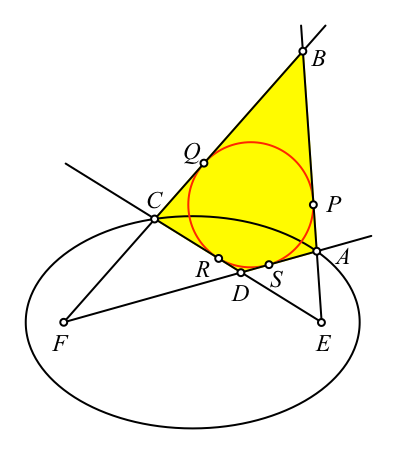
Abb. 5: Tangentenviereck?

Den Beweis führen wir indirekt, indem wir zum Beispiel annehmen, dass der Kreis, welcher drei der vier Seiten berührt, über die vierte Seite hinausreicht (Abb. 6). (Falls der Kreis zu klein ist, kann entsprechend argumentiert werden).

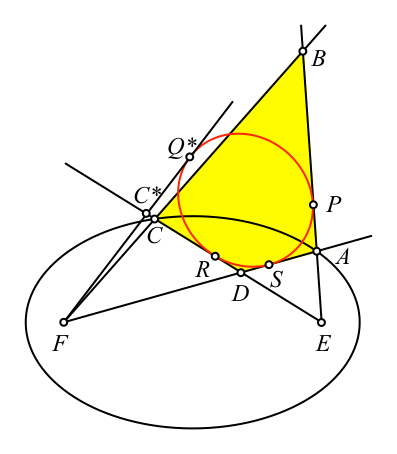
Abb. 6: Annahme: Kein Tangentenviereck

Nun kann wie oben gezeigt werden, dass AE + AF = C*F + C*E. Damit müsste der Punkt C* auf der Ellipse liegen, was er aber nicht tut.

Das Viereck ist also ein Tangentenviereck.

Analog funktioniert es mit der Hyperbel als Startfigur (Abb. 7 und 8).

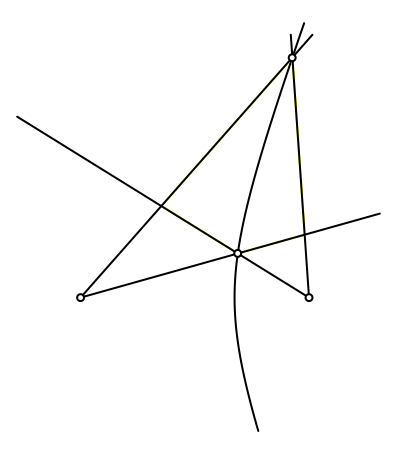
Abb. 7: Zwei Punkte auf der Hyperbel

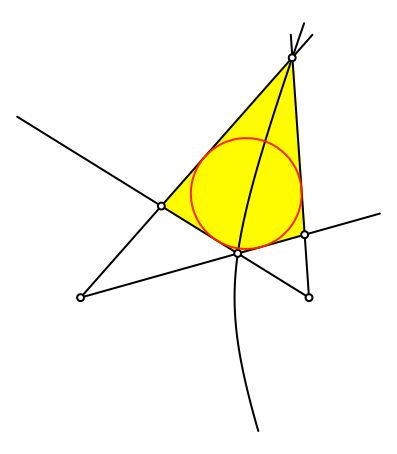
Abb. 8: Tangentenviereck