Hans Walser, [20150837]

Tangentenfünfeck

1 Worum geht es?

Zu fünf gegebenen Strecken gibt es im Prinzip genau ein passendes Tangentenfünfeck.

Ein Gelenkmodell aus fünf vorgegebenen Strecken hat also im Prinzip genau eine Tangentenfünfeckposition.

Es werden verschiedene Verfahren zur Konstruktion dieses Tangentenfünfeckes angegeben. Wir arbeiten mit DGS (dynamische Geometrie Software), mit CAS (Computer-Algebra-System) und mit HOG (hands on geometry).

Bemerkung 1: Natürlich müssen die fünf Strecken die Fünfeckbedingung erfüllen. Jede Strecke muss kürzer sein als die Summe der vier anderen.

Bemerkung 2: Die Situation ist völlig anders als beim Tangentenviereck. Beim Tangentenviereck muss die alternierende Seitensumme verschwinden. Dann gibt es aber gleich unendlich viele Tangentenvierecke.

2 Vorbereitung

Es seien also fünf Strecken (Indizes modulo 5), gegeben, welche die Fünfeckbedingung erfüllen.

Nun zeichnen wir ein beliebiges Fünfeck mit den vorgegebenen Seitenlängen (Indizes modulo 5). Dieses Fünfeck ist natürlich in aller Regel kein Tangentenfünfeck (Abb. 1). Ein Kreis, der drei aufeinanderfolgende Seiten berührt, berührt die übrigen Seiten nicht.

Abb. 1: Beliebiges Fünfeck mit vorgegebenen Seiten

Weiter wählen wir auf der Seite einen beliebigen Punkt und dazu einen Bogen mit auf der Seite dem Zentrum (Abb. 2).

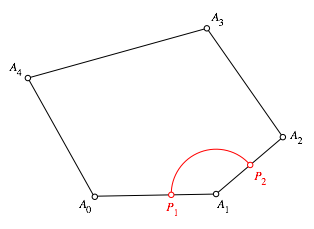
Abb. 2: Startpunkt und Bogen

Und nun bögeln wir durch gemäß Abbildung 3. Wir erhalten einen Endpunkt auf der Seite . Weiter zeichnen wir als Mittelpunkt der Strecke . Man beachte, dass nicht der Mittelpunkt der Strecke ist.

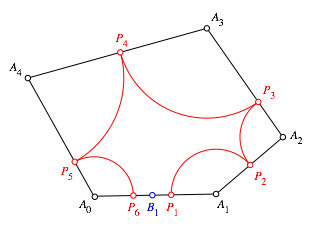
Abb. 3: Bogenfolge. Mittelpunkt

Wenn wir nun mit dem Punkt als Startpunkt die analoge Bogenfolge zeichnen, schließt sich die Figur (Abb. 4).

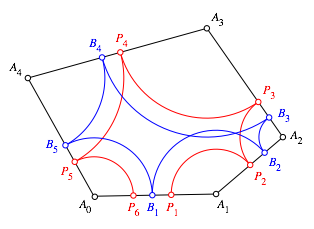
Abb. 4: Schließungsfigur

Die Schließungseigenschaft ist unmittelbar einsichtig. Sie hängt wesentlich davon ab, dass die Eckenzahl fünf eine ungerade Zahl ist. Die analoge Schließungsfigur ergibt sich bei jedem Vieleck mit ungerader Eckenzahl.

Die Leserin oder der Leser kann sich die Situation in Vielecken mit gerader Eckenzahl überlegen.

3 Was sollen diese Vorbereitungen?

Unser Fünfeck (Abb. 1 – 4) ist kein Tangentenfünfeck. Wenn wir uns aber nun ein echtes Tangentenfünfeck mit den Berührungspunkten (Indizes modulo 5) vorstellen, sehen wir gleich, dass dort die entsprechende Schließungsfigur auch funktioniert, da die beiden von einer Ecke ausgehenden Tangentenabschnitte jeweils gleich lang sind. Unsere Punkte haben also die korrekte Position der Berührungspunkte. Leider stimmt aber die Lage der Seiten noch nicht.

4 Etwas Rechnung

An dieser Stelle ist etwas Rechnung passend.

Zunächst definieren wir s als den halben Umfang:

(1)

Weiter sei der Radius des ersten roten Bogens in den Abbildungen 2 und 3. Dann ist:

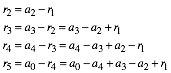(2)

Weiter ist:

(3)

Damit erhalten wir für den Mittelpunkt der Strecke :

(4)

Der Radius fällt heraus, das heißt die Position des Punktes ist irrelevant.

Unter Verwendung von (4) kann der Punkt direkt konstruiert werden, ohne den Umweg gemäß Abbildung 3.

Analog finden wir:

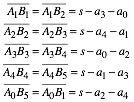(5)

oder allgemein (Indizes modulo 5):

(6)

Diese Formeln erinnern an die einschlägigen Formeln beim Dreiecksinkreis.

5 Tangentenfolge

Wir zeichnen eine Tangentenfolge wie folgt: Aus der Figur der Abbildung 3 übernehmen wir die Strecke und darauf den Punkt . In errichten wir die Senkrechte zur Strecke und wählen darauf einen Punkt M. Dann zeichnen wir den Kreis k mit Mittelpunkt M durch (Abb. 5). Die Strecke ist tangential an den Kreis k.

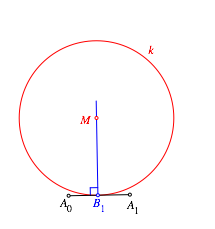
Abb. 5: Konstruktionsstart

Nun zeichnen wir von aus die zweite Tangente an den Kreis k. Darauf tragen wir von aus die Strecke ab und erhalten so den Punkt (Abb. 6).

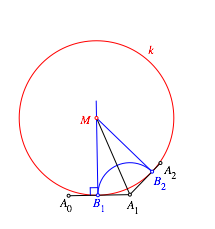
Abb. 6: Erster Schritt

Den Berührungspunkt finden wir entweder durch Spiegeln von an der Strecke oder mit einem Bogen gemäß Abbildung 6. Das ist nicht mehr der Punkt gleichen Namens wie in der Abbildung 4.

Nun fahren wir entsprechend weiter, bis wir zum Punkt gelangen (Abb. 7). Weiter geht es nicht mehr, da wir die Strecken aufgebraucht haben.

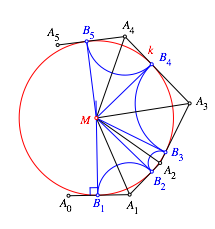
Abb. 7: Endsituation

Nun sollte aber auf zu liegen kommen, wie die Abbildung 8 suggeriert.

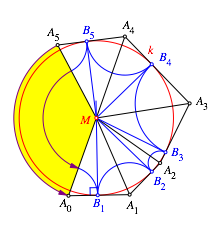
Abb. 8: Wunschtraum

Es gibt zwei Möglichkeiten dazu.

6 Die Pyramide

Wir schneiden im Prinzip (bis auf eine Klebe- oder Fixierlasche) den gelben Sektor weg. Dann falten wir längs der schwarzen Linien und erhalten so den Mantel einer (unregelmäßigen) geraden Fünfkant-Pyramide. Das Bodenfünfeck dieser Pyramide ist das gesuchte Tangentenfünfeck.

Im Anhang ein Schnittmuster. Die Klebe- oder Fixierlasche ist lila getönt. Sie kommt unter die Seitenfläche zu liegen und kann entweder verklebt (irreversibel) oder mit einer Büroklammer fixiert werden. Im Unterricht ist die Fixation mit einer Büroklammer zu empfehlen. Das Modell kann dann wieder auseinandergenommen werden. Die Abbildung 9 zeigt die aus dem Schnittmuster im Anhang gebaute Pyramide. Das Bodenfünfeck ist aus der Sicht von oben gut zu erkennen. Allenfalls muss die Pyramidenspitze mit dem Zeigefinger etwas nach unten gedrückt werden, damit sich das Bodenfünfeck schön eben ausbildet. Die blauen Geraden sind Falllinien (Linien, auf denen es am steilsten hinuntergeht) der Seitenflächen der Pyramide.

Abb. 9: Pyramide

Die Projektionen des roten Kreises k und der blauen Bogen auf die Bodenebene sind keine Kreise, sondern Ellipsen. Der Inkreis des Tangentenfünfecks ist also nicht sichtbar.

7 Einschiebekonstruktion

In der Abbildung 8 ist offensichtlich der Kreis k zu groß. Wir verkleinern ihn, indem wir den Punkt M nach unten schieben. Dies setzt DGS voraus. Die Abbildungen 10 und 11 zeigen zwei Zwischenstationen.

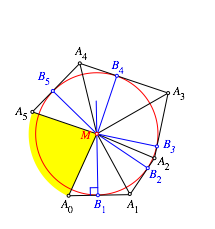
Abb. 10: Zwischenstation

Der Radius des Inkreises wird dabei kleiner.

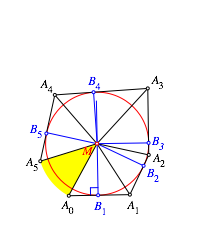
Abb. 11: Weitere Zwischenstation

Die Abbildung 12 zeigt die Endlage, also das Tangentenfünfeck mit den gegebenen Seitenlängen.

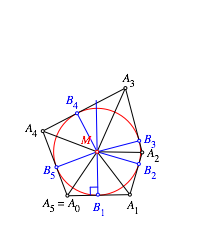
Abb. 12: Tangentenfünfeck

8 Ortskurven

Bei unserem Einschiebeverfahren bleiben die Basispunkte und fest. Die übrigen Eckpunkte bewegen sich. Die Ortskurve des Punktes ist der Kreis um mit dem Radius (Zyan in Abb. 13).

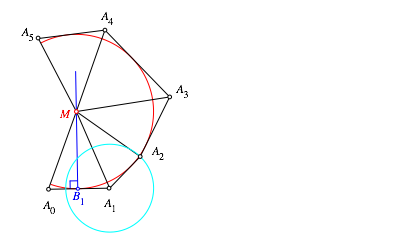
Abb. 13: Kreis als Ortskurve

Die Ortskurve von resultiert aus einer Überlagerung zweier Kreisbewegungen (Blau in Abb. 14). Sie hat einen Doppelpunkt.

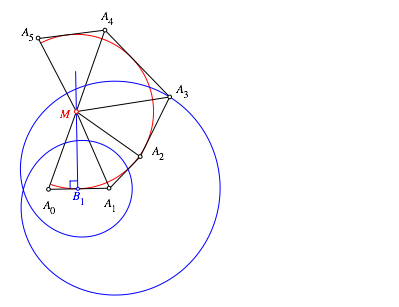
Abb. 14: Überlagerung zweier Kreisbewegungen

Die Ortskurve von resultiert aus einer Überlagerung dreier Kreisbewegungen (Dunkelgrün in Abb. 15). Sie hat einen Dreifachpunkt und einen Doppelpunkt.

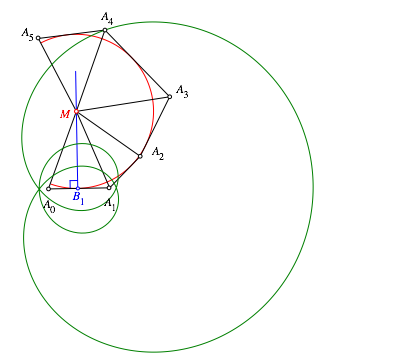
Abb. 15: Überlagerung dreier Kreisbewegungen

Die Ortskurve von ist gar eine Überlagerung von vier Kreisbewegungen (Lila in Abb. 16). Sie hat einen Vierfachpunkt und einen Dreifachpunkt.

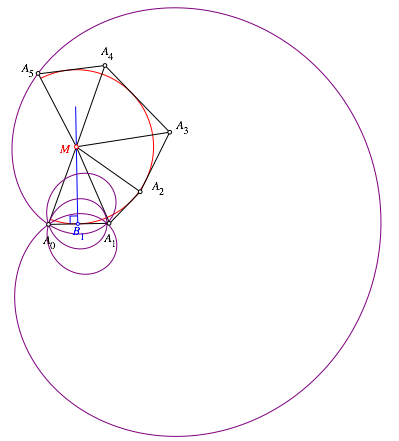
Abb. 16: Überlagerung von vier Kreisbewegungen

Der Vierfachpunkt liegt genau im Punkt . Das heißt aber, dass unser Problem vier Lösungen hat, da es vier Möglichkeiten gibt, in denen mit zusammenfällt. Wie sehen diese vier Lösungen aus?

9 Die vier Lösungen

Die Abbildung 17 zeigt die vier Situationen, in denen der Punkt mit zusammenfällt. Die Abbildung 17a entspricht dem Beispiel der Abbildung 12. Der Umlaufsinn der Eckpunkte ist positiv. Die Abbildung 17b zeigt eine Sternlösung mit positivem Umlaufsinn. Auf einem vollen Rundgang längs der Seiten wird der Inkreis zweimal umrundet. Die Abbildungen 17c und 17d zeigen symmetrische Lösungen zu den Lösungen der Abbildungen 17b und 17a. Der Umlaufsinn ist negativ.

Die Sternlösungen sind unregelmäßige Pentagramme.

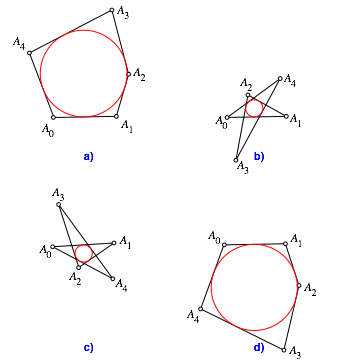
Abb. 17: Die vier Lösungen

10 Gelenkmodell

Wir bauen ein Gelenkmodell mit

(7)

Die Abbildung 18a zeigt das Gelenkmodell. In der dargestellten Position ist es offensichtlich kein Tangentenfünfeck.

Abb. 18: Gelenkmodell

Mit (5) können wir auch die Position der Berührungspunkte im Tangentenfünfeckfall ausrechnen. In der Abbildung 18b sind diese Berührungspunkte markiert.

Die Tangentenfünfeck-Position finden wir indem das Gelenkmodell über einen Kegel stülpen bis zum Anschlag (Abb. 19).

Abb. 19: Tangentenfünfeck

Wir sehen, dass unsere theoretisch berechneten Berührungspunkte durchaus am richtigen Ort sind.

11 Rechnerische Lösung

Bei gegebenen Seitenlängen des Fünfeckes können wir mit (5) die Positionen der Berührungspunkte auf den Seiten berechnen. Somit fehlt nur noch der Inkreisradius r. Die Abbildung 20 gibt die dazu nötigen Angaben.

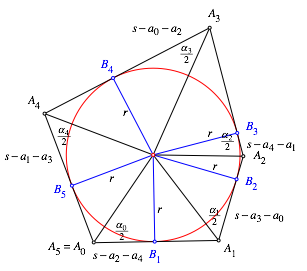
Abb. 20: Beschriftungen und Angaben

Es ist:

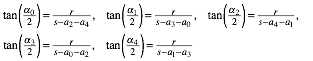(8)

Wegen der Innenwinkelsumme im Fünfeck ergibt sich aus (8):

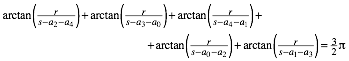(9)

Das ist eine Gleichung für r, die wir mit CAS lösen.

Im allgemeinen Fall ergibt sich eine sehr lange Formel für r. Daher im Folgenden nur der numerische Fall (7) unseres Gelenkmodells der Abbildungen 18 und 19.

restart:

a[0]:=10; a[1]:=9; a[2]:=8; a[3]:=7; a[4]:=6;

a[5]:= a[0]: a[6]:= a[1]:

s:=1/2*(a[0]+a[1]+a[2]+a[3]+a[4]);

glg:=sum(arctan(r/(s-a[k mod 5]-a[(k+2) mod 5])), k=0..4)=3/2*Pi;

r=solve(glg, r);

Wir erhalten:

Abb. 21: Ergebnis

12 Konstruktion

Die Abbildung 22 skizziert die Konstruktion des Inkreisradius r und damit des Tangentenfünfeckes. Dabei wird verwendet, dass die Zahlen 41 = 25 + 16 und 17 = 16 + 1 beide Summen von Quadraten sind.

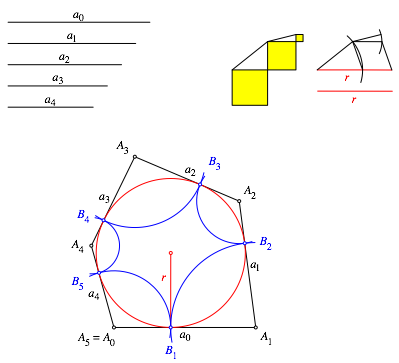
Abb. 22: Konstruktion

Das Resultat stimmt mit dem Resultat der Abbildung 19 überein.

Und die Sternlösung?

In einem Pentagramm ist die Innenwinkelsumme nur π. Wir haben die Gleichung (9) entsprechend zu modifizieren (Abb. 23).

Abb. 23: Modifikation für Pentagramm

Die Abbildung 24 zeigt die zugehörige Konstruktion.

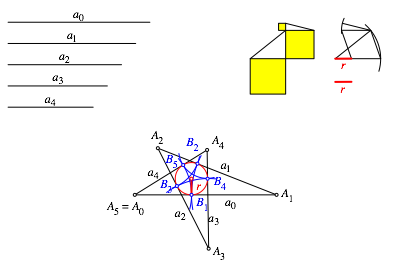
Abb. 24: Pentagramm-Stern

Die Abbildung 25 zeigt das entsprechende Gelenkmodell auf dem Kegel. Die Berührungspunkte sind dieselben wie in der Abbildung 19.

Abb. 25: Weihnachten kommt bestimmt

13 Kommentare zu den Konstruktionsverfahren

Einschiebelösungen oder Überstülpungen sind keine Lösungen im klassischen Sinn „mit Zirkel und Lineal“. Aber bereits Archimedes hat für die Winkeldrittelung eine Einschiebelösung gefunden. Das Schnittmuster der Abbildung 8 und im Anhang ist zwar mit Zirkel und Lineal konstruierbar. Aber das Ausrichten der Pyramide auf eine ebene Grundfläche ist ebenfalls nur eine Einschiebelösung.

Das Pyramidenverfahren ist für die Sternlösung ungeeignet, weil sich die Seitenflächen der Pyramide gegenseitig durchdringen müssten.

14 Ausblick

Bei Tangentenvielecken muss die Parität der Eckenzahl unterschieden werden.

14.1 Ungerade Eckenzahl

Die für das Tangentenfünfeck beschriebenen Verfahren lassen sich auf Tangentenvielecke mit ungerader Eckenzahl übertragen. Es gibt dabei noch weitere Sternlösungen. Bei sieben Ecken etwa kann der Inkreis zweimal oder gar dreimal umrundet werden.

14.2 Gerade Eckenzahl

Eine notwendige aber (mit Ausnahme des Tangentenvierecks) nicht hinreichende Bedingung ist das Verschwinden der alternierenden Seitensumme. Wenn diese Bedingung aber erfüllt ist gibt es für ein Gelenkmodell gleich unendlich viele Positionen mit einem Inkreis.

Die Abbildung 26 zeigt exemplarisch zwei verschiedene gleichseitige Tangentensechsecke.

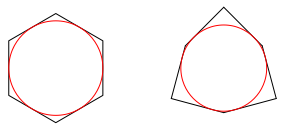
Abb. 26: Tangentensechsecke gleicher Seitenlänge

Anhang

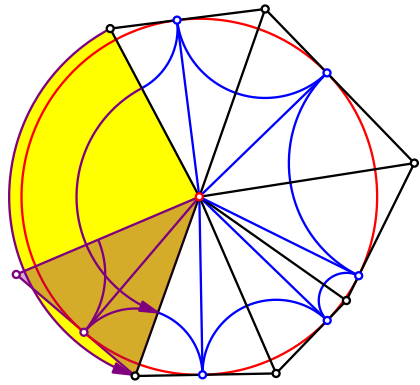
Schnittmuster für die Fünfkant-Pyramide