Hans Walser, [20180619]
Tangenten an Ellipse und Hyperbel
1 Worum geht es?
Es wird eine einfache Konstruktion der Tangenten von einem Punkt an eine Ellipse oder eine Hyperbel gezeigt.
2 Ellipse
Von einer Ellipse seien die beiden Brennpunkte F1 und F2 und der lange Durchmesser 2a gegeben (Abb. 1a). Von einem Punkt P aus sollen die Tangenten an die Ellipse konstruiert werden.
Vorgehen: Wir zeichnen um F1 und F2 je einen Kreis l1 beziehungsweise l2 mit dem Radius 2a (Abb. 1a). Weiter zeichnen wir um P je einen Kreis k1 und k2 durch F1 beziehungsweise F2. Weiter arbeiten wir mit den Schnittpunkten Qi,j gemŠ§ Abbildung 1b.
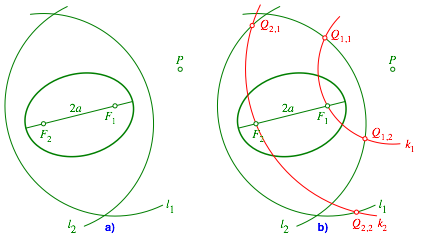
Abb. 1: Kreise
Weiter sei B1 der Schnittpunkt der Strecken F1Q2,1 und F2Q1,1 (Abb. 2a). Dieser Punkt liegt auf der Ellipse und ist der Berźhrungspunkt fźr die Tangente t1 (Abb. 2b). Analog fźr die zweite Tangente.
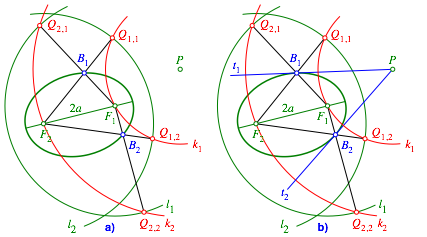
Abb. 2: Berźhrungspunkte und Tangenten
Beweis mit den Abstands- und Reflexionseigenschaften der Ellipse.
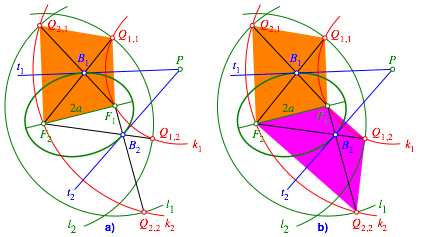
Abb. 3: Beweisfigur
Das in der Abbildung 3 orange markierte Viereck ist gemŠ§ Konstruktion ein gleichschenkliges Trapez. Daher hat der Streckenzug F1B1F2 die gleiche LŠnge wie die Diagonale F1Q2,1, also 2a. Somit liegt der Punkt B1 auf der Ellipse (Abstandseigenschaft). Weiter ist t1 Symmetrieachse des Trapezes und damit Winkelhalbierende der beiden Diagonalen. Es ist also die Reflexionseigenschaft erfźllt, t1 ist Tangente an die Ellipse.
Analog fźr die zweite Tangente t2.
3 Hyperbel
Bei der Hyperbel geht die Konstruktion analog (Abb. 4 und 5).
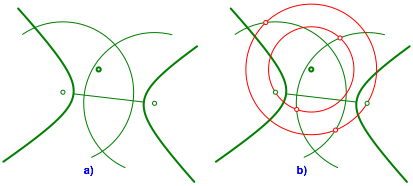
Abb. 4: Ausgangslage fźr die Hyperbel
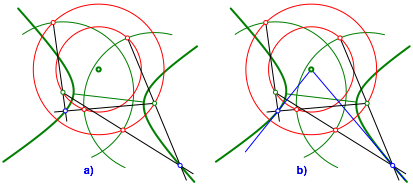
Abb. 5: Tangenten an die Hyperbel
Websites
Hans Walser: Kreistangente ohne Thaleskreis (abgerufen 18.06.2018):
www.walser-h-m.ch/hans/Miniaturen/K/Kreistangente_o_Tk/Kreistangente_o_Tk.htm