Hans Walser, [20140430]

Stochastische Matrizen

Anregung: R. S., C.

1 Doppelt stochastische Matrizen

Wir untersuchen n,n-Matrizen mit positiven Einträgen, deren Zeilen- und Spaltensummen 1 sind.

Formal:

Zeilensumme:

Spaltensumme:

2 Beispiele

2.1 Beispiel

2.2 Magische Quadrate

Aus magischen Quadraten lassen sich durch Normierung mit der Zeilensumme doppelt stochastische Matrizen herstellen. Dabei sind dann zusätzlich (das „Magische“) auch die Diagonalensummen 1.

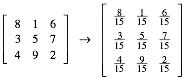
Aus dem im Prinzip einzigen magischen 3,3-Quadrat erhalten wir:

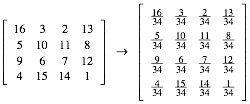
Aus dem magischen Dürer-Quadrat ergibt sich:

3 Eigenschaften

3.1 Eigenwerte und Eigenvektoren

Eine Matrix mit Zeilensumme 1 hat den Eigenwert mit dem Eigenvektor

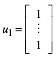
Beweis durch Nachrechnen. Es ist .

3.2 Lineare Abbildung

Wir arbeiten mit einer Abbildungsmatrix mit Spaltensumme 1.

Es sei ein Punkt in der Hyperebene H: . Wegen

erhalten wir für den Bildpunkt :

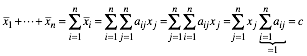
Somit liegt auch der Bildpunkt in der Hyperebene H.

Die Hyperebene H hat den Normalvektor .

3.3 Doppelt stochastische Abbildungsmatrix

Bei einer doppelt stochastischen Abbildungsmatrix haben wir einerseits die Fixpunktgerade . Andererseits operieren alle anderen Punkte in einer Normalhyperebene dazu.

4 Beispiel einer Abbildung

Wir arbeiten exemplarisch mit der Abbildungsmatrix:

In der Abbildung 1a sind im Einheitswürfel die Bilder der drei Einheitsvektoren eingetragen. Die Abbildung 1b zeigt das Bild des Einheitswürfels. Es entsteht ein Spat, der eine Raumdiagonale mit dem Einheitswürfel gemeinsam hat und sonst ganz im Innern des Einheitswürfels liegt.

Abb. 1: Situation im Einheitswürfel

Die in der Abbildung 2 markierten Punkte liegen jeweils in einer Ebene. Dies sind Normalebenen zur vom Ursprung ausgehenden Raumdiagonalen des Einheitswürfels.

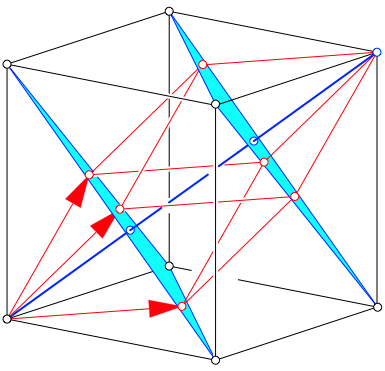
Abb. 2: Normalebenen zur Raumdiagonalen des Würfels

Die Abbildung 3 zeigt, wie die lineare Abbildung im unteren der beiden blauen Dreiecke operiert. Das ist das durch die Bilder der drei Einheitsvektoren aufgespannte Dreieck.

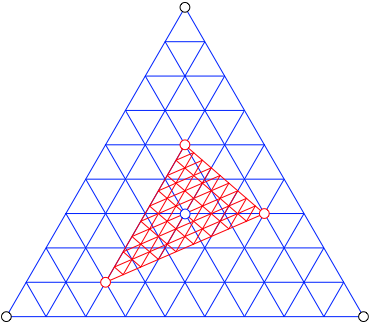
Abb. 3: Situation im unteren blauen Dreieck

Der Schwerpunkt des blauen Urbilddreiecks ist Fixpunkt, er ist auch Schwerpunkt des roten Bilddreiecks. Dieser Schwerpunkt hat im Raum die Koordinaten . Er liegt auf der Fixpunktgeraden.

Wird die Abbildung iteriert, ziehen sich die Bilder auf den Fixpunkt zusammen.

In der Abbildung 4 ist der nächste Schritt eingezeichnet.

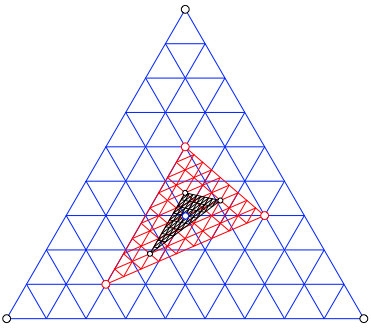
Abb. 4: Nächster Schritt

Im Limes ergeben sich für die Bilder der drei Einheitsvektoren die drei Vektoren

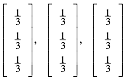
Somit ist:

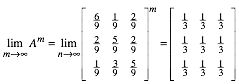
Die Kontraktionseigenschaft und damit der Limes gelten für beliebige doppelt stochastische 3,3-Matrizen.

Für die Dimension n wird das gleichseitige Dreieck durch das regelmäßige n-Simplex ersetzt. Im vierdimensionalen Fall also das regelmäßige Tetraeder.

Der Schwerpunkt hat die Koordinaten .

Allgemein gilt daher für eine doppelt stochastische n,n-Matrix A: