Hans Walser, [20131129]
Summen von Kuben
1 Worum geht es?
Wir suchen ganzzahlige LÜsungen der kubischen Gleichung:
![]()
2 Beispiele
Die Tabelle zeigt einige LÜsungen mit natčrlichen Zahlen. Die LÜsungen wurden mit brute force gefunden.
|
a |
b |
c |
d |
|
1 |
6 |
8 |
9 |
|
2 |
17 |
40 |
41 |
|
3 |
4 |
5 |
6 |
|
3 |
10 |
18 |
19 |
|
3 |
36 |
37 |
46 |
|
4 |
17 |
22 |
25 |
|
6 |
32 |
33 |
41 |
|
7 |
14 |
17 |
20 |
|
11 |
15 |
27 |
29 |
|
15 |
42 |
49 |
58 |
|
16 |
23 |
41 |
44 |
|
18 |
19 |
21 |
28 |
|
27 |
30 |
37 |
46 |
|
29 |
34 |
44 |
53 |
3 Illustration
Die Abbildung 1 illustriert das einfachste Beispiel: a = 3, b = 4, c = 5 und d = 6.

Abb. 1: Gelb + Blau + Rot = Grčn
Die Abbildung 2 zeigt in mehreren Schritten den Umbau von Gelb + Balu + Rot in Grčn.
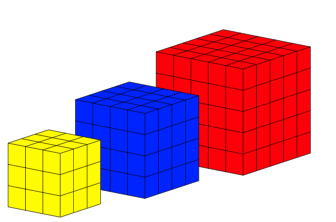
Abb. 2.1: Ausgangslage
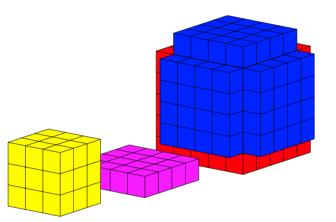
Abb. 2.1: Erster Schritt
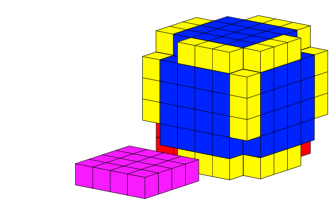
Abb. 2.2: Zweiter Schritt

Abb. 2.3: Dritter Schritt
Projekt: Kuben analog zum Soma-Wčrfel (hier der gelbe Wčrfel) zerlegen.
4 Negative Zahlen
Wir
lassen nun zu, dass c und allenfalls d negativ sind. Dabei soll aber ![]() sein, um
triviale LÜsungen zu vermeiden. Die Tabelle zeigt einige LÜsungen:
sein, um
triviale LÜsungen zu vermeiden. Die Tabelle zeigt einige LÜsungen:
|
a |
b |
c |
d |
|
a |
b |
c |
d |
|
1 |
12 |
-10 |
9 |
|
12 |
40 |
-33 |
31 |
|
1 |
12 |
-9 |
10 |
|
12 |
40 |
-31 |
33 |
|
2 |
16 |
-15 |
9 |
|
15 |
33 |
-34 |
2 |
|
2 |
16 |
-9 |
15 |
|
15 |
33 |
-2 |
34 |
|
2 |
34 |
-33 |
15 |
|
16 |
33 |
-34 |
9 |
|
2 |
34 |
-15 |
33 |
|
16 |
33 |
-9 |
34 |
|
9 |
10 |
-12 |
1 |
|
17 |
39 |
-36 |
26 |
|
9 |
10 |
-1 |
12 |
|
17 |
39 |
-26 |
36 |
|
9 |
15 |
-16 |
2 |
|
19 |
24 |
-27 |
10 |
|
9 |
15 |
-2 |
16 |
|
19 |
24 |
-10 |
27 |
|
9 |
34 |
-33 |
16 |
|
26 |
36 |
-39 |
17 |
|
9 |
34 |
-16 |
33 |
|
26 |
36 |
-17 |
39 |
|
10 |
27 |
-24 |
19 |
|
31 |
33 |
-40 |
12 |
|
10 |
27 |
-19 |
24 |
|
31 |
33 |
-12 |
40 |
Wir sehen, dass sich etliche LÜsungen bis auf Vorzeichenkombinationen und Anordnung wiederholen, so zum Beispiel:
|
a |
b |
c |
d |
|
1 |
12 |
-10 |
9 |
|
1 |
12 |
-9 |
10 |
|
9 |
10 |
-12 |
1 |
|
9 |
10 |
-1 |
12 |
Diese
LÜsung kann auch in der Form ![]() geschrieben werden. Einer Anekdote
zufolge soll Ramanujan gegenčber Hardy geŐužert haben, die von Hardy als
Ńnichtssagende ZahlĎ bezeichnete Zahl 1729 sei die kleinste Zahl, welche als
Summe von zwei Kuben geschrieben werden kann, eben
geschrieben werden. Einer Anekdote
zufolge soll Ramanujan gegenčber Hardy geŐužert haben, die von Hardy als
Ńnichtssagende ZahlĎ bezeichnete Zahl 1729 sei die kleinste Zahl, welche als
Summe von zwei Kuben geschrieben werden kann, eben ![]() .
.

Srinivasa Aiyangar Ramanujan, 1887 – 1920
Literatur
Harper, James, F.: Ramanujan, Quadratic Forms,
and the Sum of three Cubes. Math. Mag. 86 (2013) 275-279. doi:10. 4169 / math.mag.
86. 4. 275. ę Mathematical Association of America