Hans Walser, [20181103], [20181216]

Stetige Teilung

1 Worum geht es?

Die Euklidische Definition der stetigen Teilung wird verallgemeinert.

2 Euklid

Eine Strecke heißt stetig geteilt (Walser 2013, S. 13), wenn für die Teilstrecken und mit gilt:

(1)

Die Abbildung 1 illustriert den Sachverhalt.

Abb. 1: Stetige Teilung

Man spricht in dieser Situation auch von der Teilung im Goldenen Schnitt.

3 Drei Teile

Wir arbeiten mit drei Teilstücken , und mit , und es soll gelten:

(2)

Die Abbildung 2 illustriert den Sachverhalt.

Abb.3: Drei Teile

4 Allgemeint mit n Teilen

Wir arbeiten mit n Teilstücken , und es soll gelten:

(3)

Die Abbildung 3 illustriert den Sachverhalt für n = 2, 3, ... , 10.

Abb. 3: Stetige Teilungen

Die Abbildung 4 zeigt dasselbe mit Balkendiagrammen.

Abb. 4: Stetige Teilungen

5 Numerisches

Die Gleichung (3) beinhaltet nur Gleichungen für die n Unbekannten . Wir führen als weitere Gleichung die Normierung

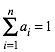(4)

ein.

Das aus (3) und (4) bestehende Gleichungssystem ist nicht linear. Dies macht das Auflösen schwierig.

5.1 Zwei Teile

Für n = 2 erhalten wir die Werte der Tabelle 1.

i
1	0.3819660113
2	0.6180339887

Tab. 1: Zwei Teile

Wir erhalten die Werte des Goldenen Schnittes.

5.2 Drei Teile

Für n = 3 erhalten wir die Werte der Tabelle 2.

i
1	0.19806226419515996
2	0.3568958678922133
3	0.4450418679126268

Tab. 2: Drei Teile

Die drei Teile bilden keine geometrische Folge.

5.3 Vier Teile

Für n = 4 erhalten wir die Werte der Tabelle 3.

i
1	0.12061475842818324
2	0.22668159690567746
3	0.30540728933227856
4	0.3472963553338607

Tab. 3: Vier Teile

5.4 Fünf Teile

Für n = 5 erhalten wir die Werte der Tabelle 4.

i
1	0.08101405277100522
2	0.15546482879562723
3	0.21732076897616492
4	0.2615706729106323
5	0.2846296765465703

Tab. 4: Fünf Teile

6 Link mit Trigonometrie

Wir führen für i = 1, ..., n und m = 2n +1 drei neue Folgen ein:

(5)

(6)

(7)

Die Tabelle 5 zeigt die Werte für n = 5.

i
1	0.08101405280	0.1554648288	0.08101405288
2	0.1554648288	0.2615706730	0.1554648289
3	0.2173207690	0.2846296766	0.2173207692
4	0.2615706730	0.2173207690	0.2615706732
5	0.2846296766	0.08101405280	0.2846296763

Tab. 5: Zwei neue Folgen

Wir vermuten, dass die Folgen und untereinander und mit der Folge übereinstimmen. Die Folge hat dieselben Werte wie die anderen Folgen, aber sie sind anders angeordnet. Die größte Zahl ist in der Mitte.

Die Gleichwertigkeit der drei Folgen kann mit trigonometrischen Mitteln bewiesen werden. Siehe dazu [1].

Für die Übereinstimmung mit der Folge muss gezeigt werden, dass die Bedingungen (3) und (4) erfüllt sind. Dazu habe ich CAS verwendet. Ein formaler Beweis ist mir nicht gelungen.

7 Link mit Geometrie

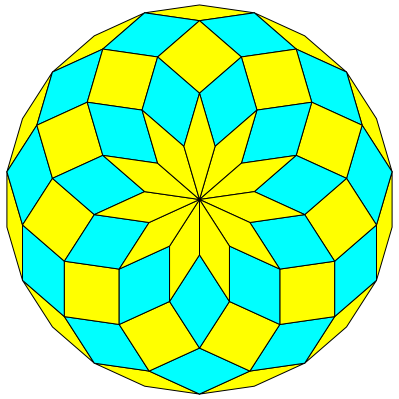
Abb. 5: Rhombenrosette

Die Rhombenrosette der Abbildung 5 besteht aus n = 5 Ringen mit je m = 2n +1 = 11 Rhomben. Die dem Zentrum zugewandten Rhombenwinkel sind der Reihe nach:

(8)

Also:

(9)

Für die Flächeninhalte der Rhomben im i-ten Ring erhalten wir daraus:

(10)

Dabei ist s die Seitenlänge der Rhomben. Wir sehen, dass die Flächenverhältnisse der Folge entsprechen. Der Flächenanteil des äußersten Ringes mit den kleinsten Rhomben ist etwa 8.1%, der Flächenanteil des mittleren Ringes mit den größten Rhomben ist etwa 28.5%.

Die Flächenverhältnisse entsprechen der verallgemeinerten stetigen Teilung.

Literatur

Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Weblinks

[1] Hans Walser: Trigonometrische Identität

http://www.walser-h-m.ch/hans/Miniaturen/T/Trigo_Id/Trigo_Id.htm