1 Worum geht es?

Variante zum Sierpiński-Dreieck

2 Unterteilung des Dreiecks

Durch Halbieren der Seiten kann das gleichseitige Dreieck in vier Teildreiecke unterteilt werden. Der Prozess kann iteriert werden (Abb. 1 und 2).

Für Längenberechnungen setzen wir die Seitenlänge des Dreiecks auf 1.

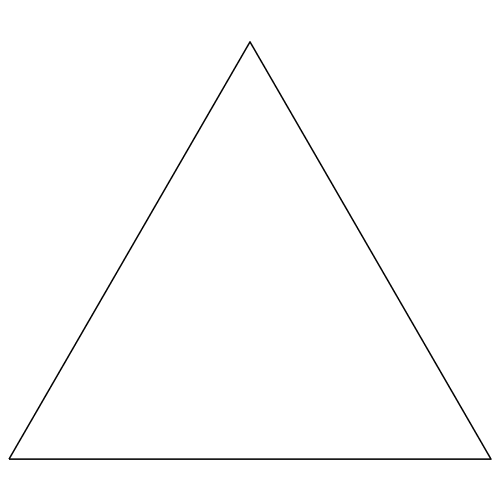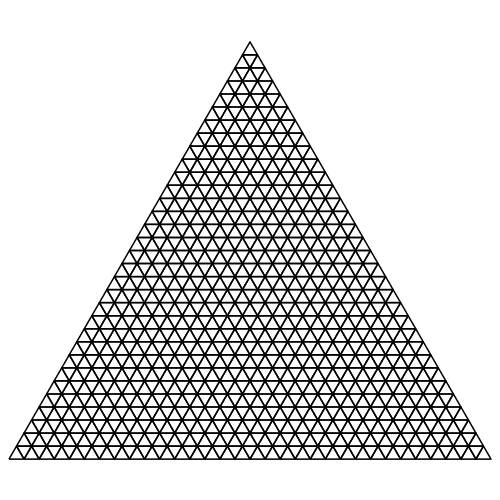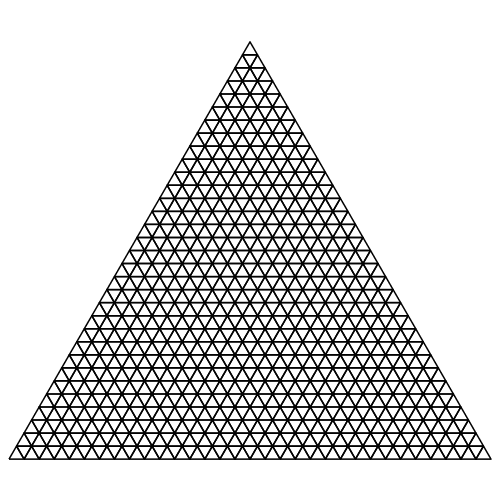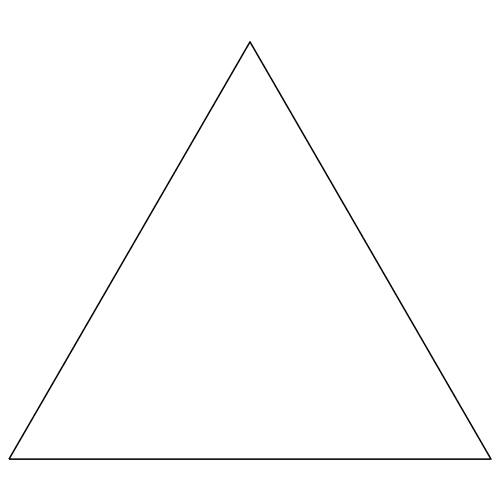
Abb. 1: Fortlaufende Unterteilung

Abb. 2: Farbige Unterteilung

3 Klassisch

Wir das jeweils mittlere Dreieck weggelassen, entsteht das klassische Sierpiński-Dreieck (Abb. 3 und 4). Es hat die fraktale Dimension D = log₂(3) ≈ 1.585.

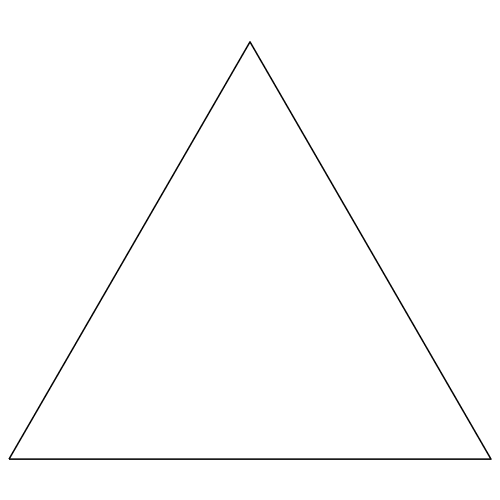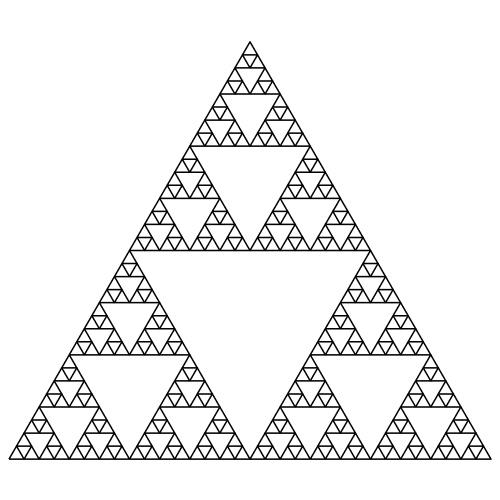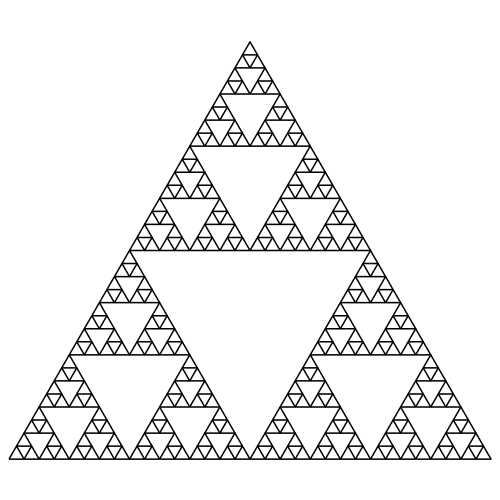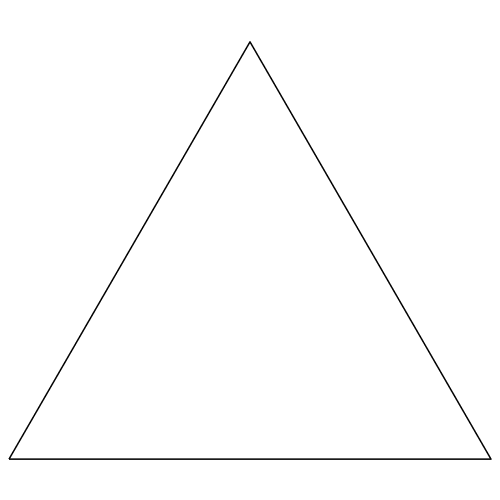
Abb. 3: Sierpiński-Dreieck

Abb. 4: Sierpiński-Dreieck in Farbe

4 Varianten

4.1 Oberstes Dreieck weglassen

Wird das jeweils oberste Dreieck weggelassen, entsteht das Fraktal der Abbildungen 5 und 6. Es hat ebenfalls die fraktale Dimension D = log₂(3) ≈ 1.585.

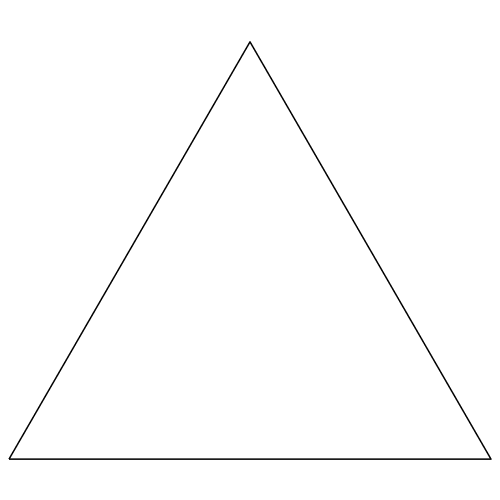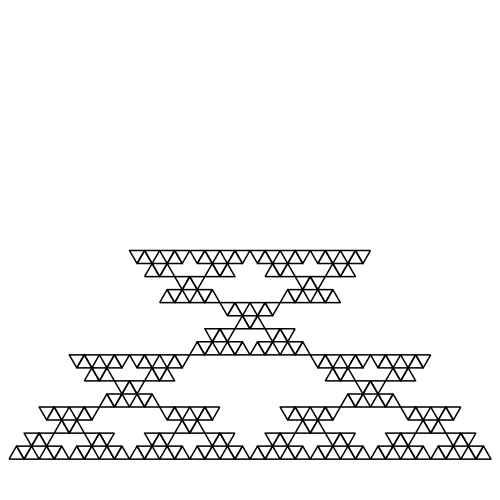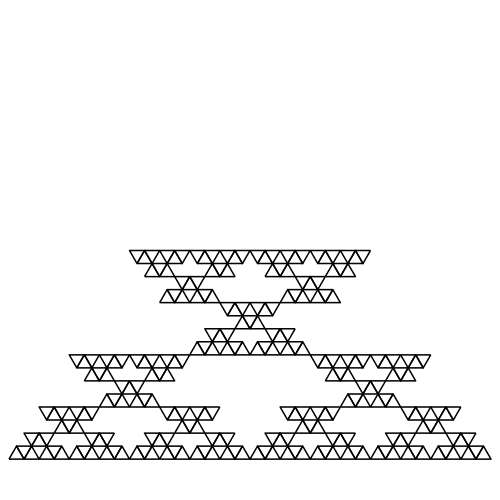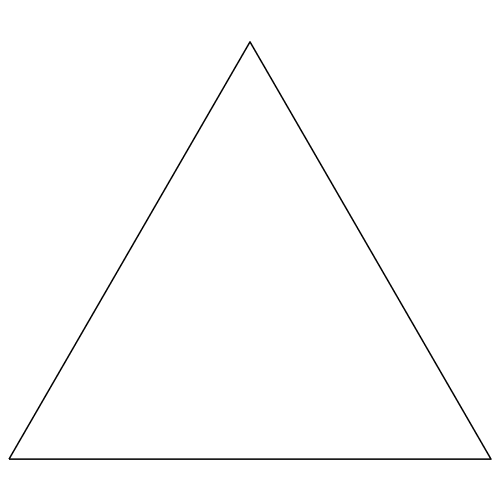
Abb. 5: Oberstes Dreieck weglassen.

Abb. 6: Dasselbe farbig

4.2 Oberstes und mittleres Dreieck weglassen

Wird das jeweils oberste Dreieck und das mittlere Dreieck weggelassen, entsteht das Fraktal der Abbildungen 7 und 8. Es hat die fraktale Dimension D = log₂(2) = 1.

Die obere Zickzacklinie hat immer die Länge 2, die untere Strecke die Länge 1.

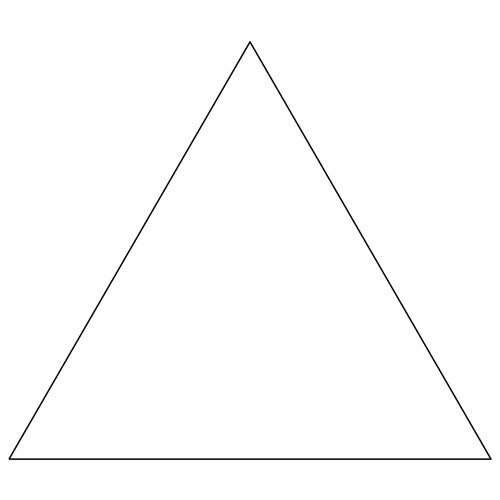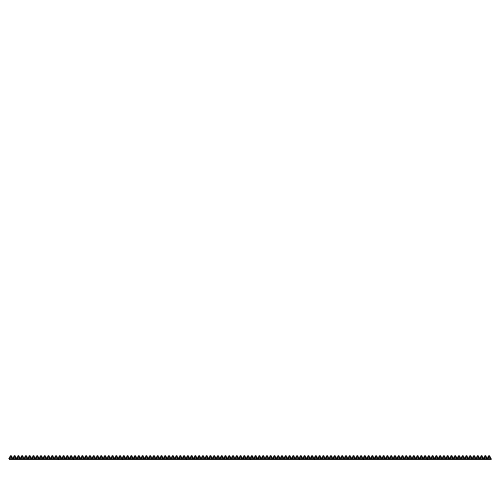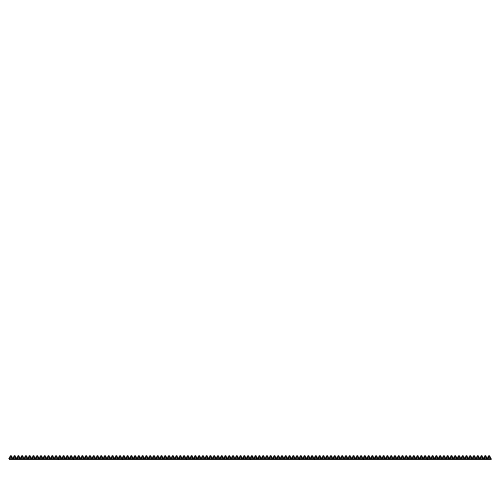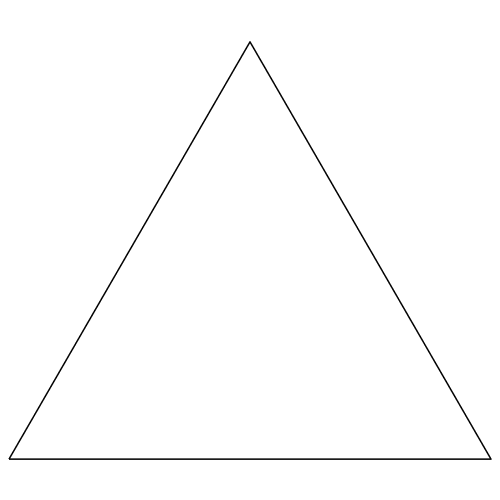
Abb. 7: Oberstes und mittleres Dreieck weglassen

Abb. 8: Dasselbe in Farbe

4.3 Linkes und rechtes Dreieck weglassen

Wird das jeweils linke Dreieck und das recbte Dreieck weggelassen, entsteht das Fraktal der Abbildungen 9 und 10. Es hat ebenfalls die fraktale Dimension D = log₂(2) = 1.

Die seitliche Zickzacklinie hat immer die Länge 1. Die Höhe der Figur ist √3/2 ≈ 0.866.

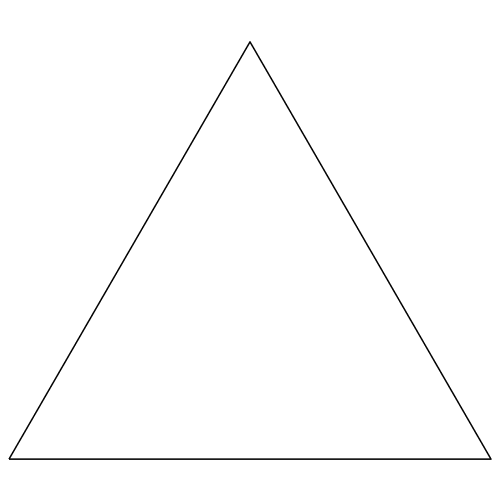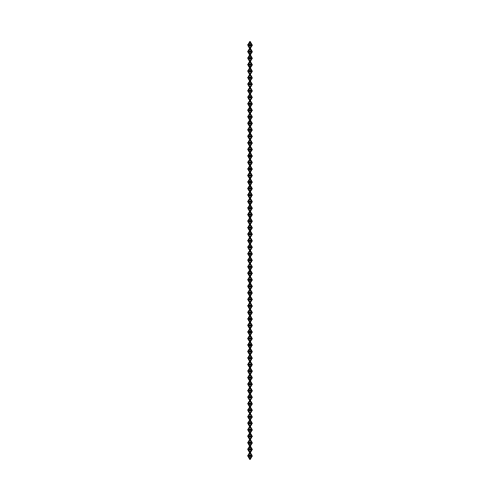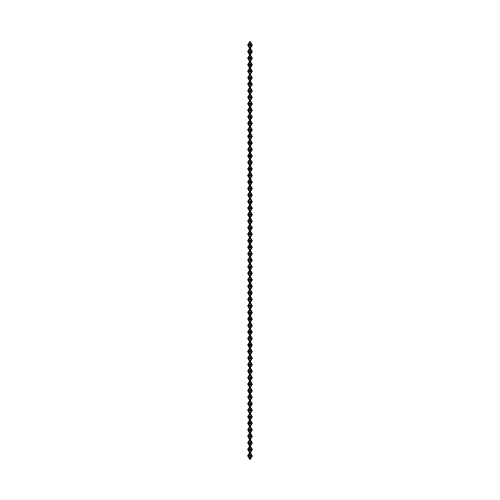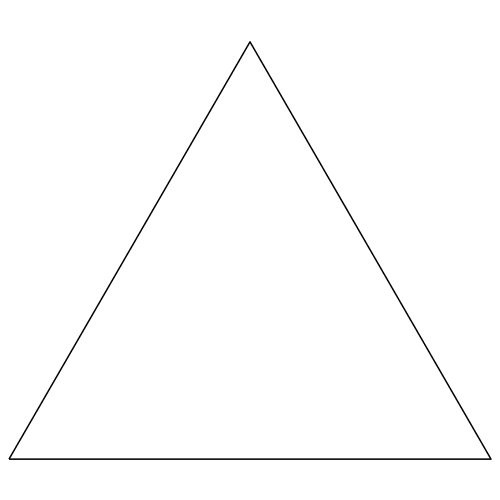
Abb. 9: Linkes und rechtes Dreieck weggelassen

Abb. 10: Dasselbe in Farbe

4.3.1 Drei Dreiecke weglassen

Wir behalten lediglich das Dreieck links. Die Figur reduziert sich auf einen Punkt. Die fraktale Dimension ist D = log₂(1) = 0.

Abb. 11: Drei Dreiecke weggelassen

Abb. 12: Dasselbe in Farbe

Weblinks

Hans Walser: Sierpiński-Fraktale

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Fraktale/Sierpinski-Fraktale.htm