Hans Walser, [20220206]

Sierpinski-Kurve

Anregung: Georg Schierscher, Schaan

1 Worum geht es?

Spielerei um die Sierpinski-Kurve. Variante

Die Sierpinski-Kurve gehört zu den Monsterkurven (Schierscher 2013, S. 48-61).

2 Konstruktion

Die Sierpinski-Kurve ist der jeweilige Rand des roten Polygons (Abb. 1 und 2).

Abb. 1: Konstruktion

Abb. 2: Generationenweise

3 Analyse

Zur Analyse der Figur ist eine zweifarbige Darstellung vorteilhaft (Abb. 3).

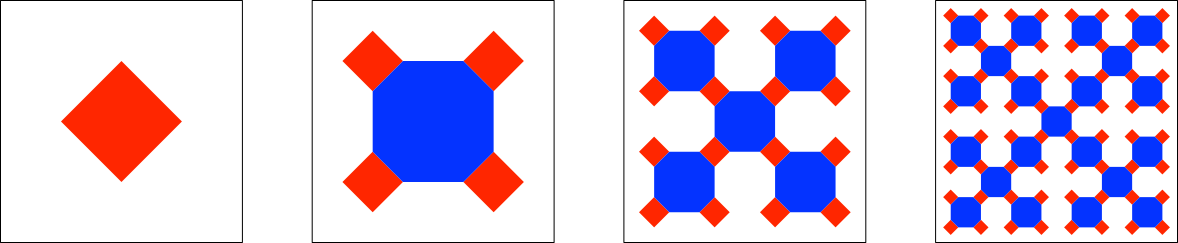
Abb. 3: Rot und blau

Abb. 4: Rot und blau generationenweise

4 Flächeninhalt

Wir berechnen die Flächeninhalte in Relation zum Flächeninhalt des schwarzen Grenzquadrates. Dieses habe also den Flächeninhalt 1.

Das rote Quadrat der Startfigur (Generation 0) hat den Flächeninhalt 1/8. Da wir von Generation zu Generation einen Längen-Skalierungsfaktor ½ haben, haben wir in jeder nachfolgenden Generation viermal so viel rote Quadrate mit je einem um den Flächen-Skalierungsfaktor ¼ reduzierten Flächeninhalt. Somit bleibt der gesamte rote Flächeninhalt von Generation zu Generation konstant. Er ist also immer 1/8.

Bei den (unregelmäßigen) blauen Achtecken ist es anders. Das erste blaue Achteck (Generation 1) hat den Flächeninhalt 7/32. Die blauen Flächeninhalte werden von Generation zu Generation nicht nur reproduziert, sondern es kommt immer noch eine neues, allerdings immer kleiner werdendes Achteck dazu (Tab. 1).

Generation	Flächeninhalt blau
0	0
1	7/32	7/32*1	7/32*(1)
2	7/32*(4*1/4 + 1/4)	7/32*5/4	7/32*(1 + 1/4)
3	7/32*(4*5/16 + 1/16)	7/32*21/16	7/32*(1 + 1/4 + 1/16)
4	7/32*(4*21/64 + 1/64)	7/32*85/64	7/32*(1 + 1/4 + 1/16 + 1/64)
5	7/32*(4*85/256 + 1/256)	7/32*341/256	7/32*(1 + 1/4 + 1/16 + 1/64 + 1/256)

Tab. 1: Flächeninhalt blau

Wir sehen die Gesetzmäßigkeit. Es entsteht eine geometrische Reihe mit dem Grenzwert 7/32*4/3 = 7/24.

Für die Gesamtfläche ergibt sich im Grenzfall 1/8 + 7/24 = 5/12. Das ist weniger als die Hälfte.

Die Umfangberechnungen haben mit sqrt(2) zu tun. Lassen wir weg.

5 Variante

Die Abbildung 5 zeigt eine Variante mit ausschließlich rechten Winkeln.

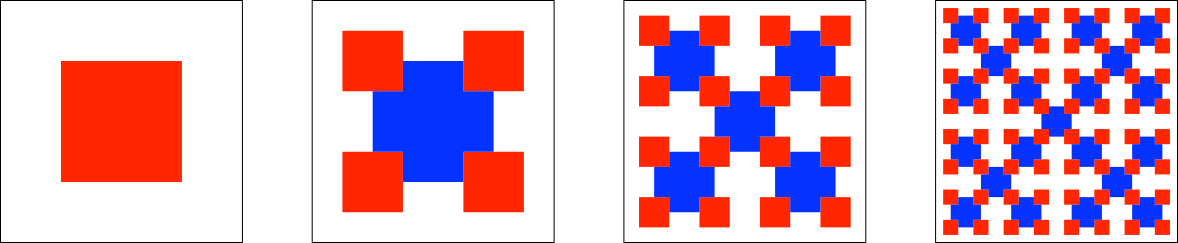
Abb. 5: Variante

5.1 Flächeninhalt

Wir berechnen die Flächeninhalte in Relation zum Flächeninhalt des schwarzen Grenzquadrates. Dieses habe also den Flächeninhalt 1.

Das rote Quadrat der Startfigur (Generation 0) hat den Flächeninhalt 1/4. Da wir von Generation zu Generation einen Längen-Skalierungsfaktor ½ haben, haben wir in jeder nachfolgenden Generation viermal so viel rote Quadrate mit je einem um den Flächen-Skalierungsfaktor ¼ reduzierten Flächeninhalt. Somit bleibt der gesamte rote Flächeninhalt von Generation zu Generation konstant. Er ist also immer 1/4.

Bei den blauen Zwölfecken ist es anders. Das erste blaue Zwölfeck (Generation 1) hat den Flächeninhalt 3/16. Die blauen Flächeninhalte werden von Generation zu Generation nicht nur reproduziert, sondern es kommt immer noch eine neues, allerdings immer kleiner werdendes Zwölfeck dazu (Tab. 2).

Generation	Flächeninhalt blau
0	0
1	3/16	3/16*1	3/16*(1)
2	3/16*(4*1/4 + 1/4)	3/16*5/4	3/16*(1 + 1/4)
3	3/16*(4*5/16 + 1/16)	3/16*21/16	3/16*(1 + 1/4 + 1/16)
4	3/16*(4*21/64 + 1/64)	3/16*85/64	3/16*(1 + 1/4 + 1/16 + 1/64)
5	3/16*(4*85/256 + 1/256)	3/16*341/256	3/16*(1 + 1/4 + 1/16 + 1/64 + 1/256)

Tab. 2: Flächeninhalt blau

Wir sehen die Gesetzmäßigkeit. Es entsteht eine geometrische Reihe mit dem Grenzwert 3/16*4/3 = 1/4.

Für die Gesamtfläche ergibt sich im Grenzfall 1/4 + 1/4 = 1/2.

5.2 Umfang

Der Umfang der rot-blauen Gesamtfigur und damit die Länge der Kurve verdoppelt sich von Generation zu Generation. Zunächst haben wir vier Kopien mit dem Längen-Skalierungsfaktor ½. Dies verdoppelt den gesamten Umfang. Allerdings fallen in der Mitte acht kleine rote Umfangteile weg, die aber durch das neu eingefügte blaue Teil gerade kompensiert werden. Die Folge der Umfänge divergiert.

Der Umfang des roten Quadrates der Generation 0 ist halb so groß wie der Umfang des schwarzen Quadrates. Bei der Generation 1 haben das Polygon und das schwarze Quadrat denselben Umfang.

5.3 Kurven

Die Abbildung 6 zeigt die ersten Kurvengenerationen.

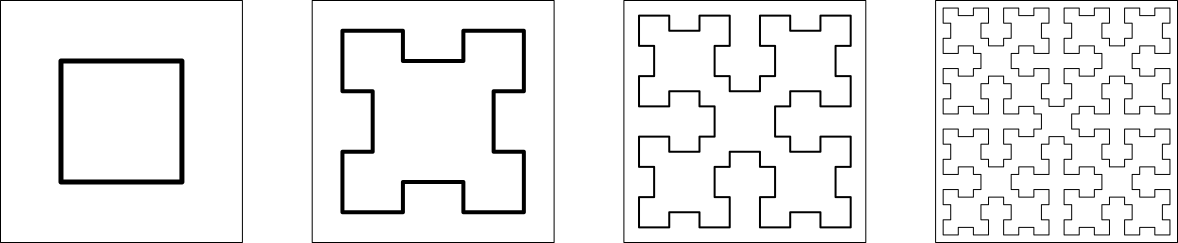
Abb. 6: Kurven

In der Abbildung 7 sind die Kurven der Generationen 0 bis 3 überlagert.

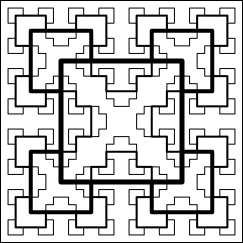
Abb. 7: Überlagerung

Die Abbildung 8 zeigt die Überlagerung je zweier aufeinanderfolgender Generationen. Die Kurve der neuen Generation fährt streckenweise auf der Kurve der alten Generation.

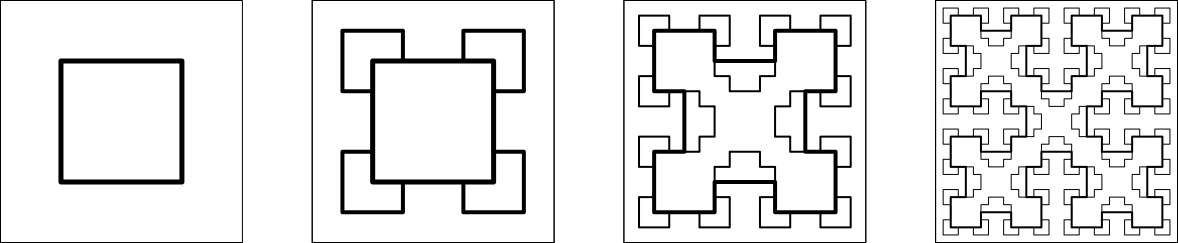
Abb. 8: Überlagerungen

5.4 Animation

Abb. 9: Animierte Variante

Literatur

Schierscher, Georg (2013): Matheliebe. Herausgeber: Rainer Vollkommer (Liechtensteinisches Landesmuseum). 2. Auflage. Vaduz: Liechtensteinisches Landesmuseum. ISBN 978-3-905437-33-1.