Hans Walser, [20200616]

Seilspirale

1 Worum geht es?

Die Abbildung 1 zeigt ein spiralförmig aufgewickeltes, etwas lädiertes Kletterseil. Auf der Seiloberfläche sehen wir eine schraubenlinienförmige schwarze Markierung. Diese Markierung führt zu zusätzlichen übergreifenden Kurven und Figuren. Was für Kurven sind das?

Abb. 1: Unsicheres Kletterseil

Die Schraubenlinie ist eine Linksschraube. Die Steigung ist ungefähr . Bei einer Rechtsschraube wäre die Steigung positiv. Für unser Problem spielt es aber grundsätzlich keine Rolle, ob wir mit Linksschrauben oder mit Rechtsschrauben arbeiten.

2 Die Schraubenlinie auf dem Kletterseil

Die Abbildung 2 zeigt der Reihe nach die Steigungen der schwarzen Markierung. Die Abbildung 2e illustriert die Steigung (auf 3 nach rechts 2 hinunter).

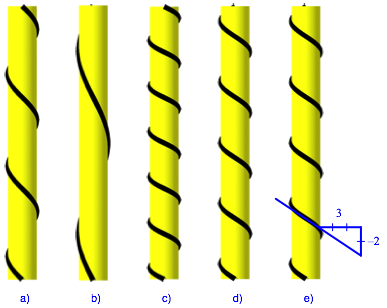
Abb. 2: Steigung der schwarzen Markierung

3 Beispiele

3.1 Steigung minus eins

Abb. 3: Steigung minus eins

Approximativ punktsymmetrische Figur (als zweidimensionale Figur aufgefasst). Die Punktsymmetrie ist nicht exakt, da der Rand der Figur keine Punktsymmetrie aufweist.

3.2 Steigung minus 2

Abb. 4: Steigung minus 2

3.3 Steigung minus ein Halb

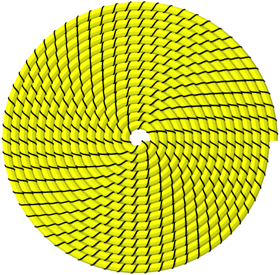
Abb. 5: Steigung minus ein Halb

Approximativ vierteilige Drehsymmetrie.

3.4 Steigung minus zwei Drittel

Abb. 6: Steigung minus zwei Drittel

Approximativ dreiteilige Drehsymmetrie

3.5 Steigung minus ein Drittel

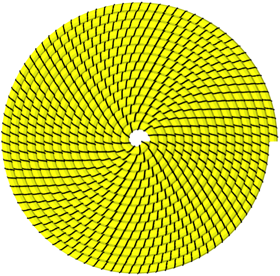
Abb. 7: Steigung minus ein Drittel

Approximativ sechsteilige Drehsymmetrie.

3.6 Steigung minus ein Viertel

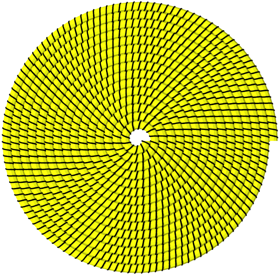
Abb. 8: Steigung minus ein Viertel

Approximativ achtteilige Drehsymmetrie.

3.7 Steigung minus ein Fünftel

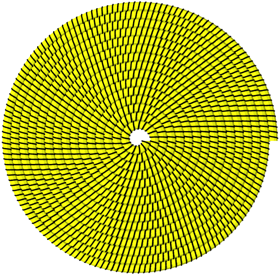
Abb. 9: Steigung minus ein Fünftel

Approximativ zehnteilige Drehsymmetrie.

3.8 Steigung minus zwei Fünftel

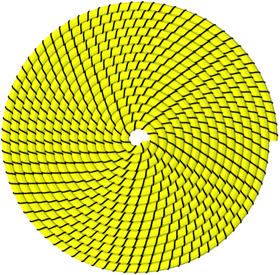
Abb. 10: Steigung minus zwei Fünftel

Approximativ fünfteilige Drehsymmetrie

3.9 Steigung minus drei Fünftel

Abb. 11: Steigung minus drei Fünftel

Approximativ Drehsymmetrie ?

3.10 Steigung minus vier Fünftel

Abb. 12: Steigung minus vier Fünftel

Approximativ fünfteilige Drehsymmetrie erkennbar?

3.11 Steigung minus ein Sechstel

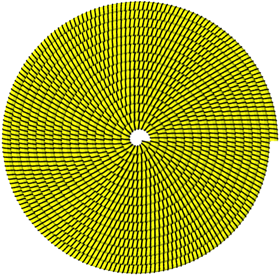
Abb. 13: Steigung minus ein Sechstel

Approximativ zwölfteilige Drehsymmetrie

3.12 Irrationale Steigung

Abb. 14: Steigung irrational

Steigung , irrational. Kein durchgehendes Muster erkennbar. Erinnert an das Kletterseil der Abbildung 1.

Websites

Hans Walser: Archimedische Spirale

http://www.walser-h-m.ch/hans/Miniaturen/A/Arch_Spirale/Arch_Spirale.htm

Hans Walser: Evolvente

http://www.walser-h-m.ch/hans/Miniaturen/E/Evolvente/Evolvente.htm