Hans Walser, [20170408]
Sehnenviereck
Anregung: H. K., O.
1 Worum geht es?
Es werden einige Spielereien um das Sehnenviereck vorgestellt. Dabei benštigen wir den Sachverhalt, dass genau in einem Sehnenviereck sich gegenźberliegende Winkel auf ą ergŠnzen. †ber Sehnenvierecke siehe auch [1].
2 Winkelhalbierende in einem beliebigen Viereck
Die Schnittfigur der Winkelhalbierenden eines beliebigen Vierecks ist ein Sehnenviereck (Abb. 1).
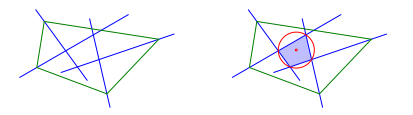
Abb. 1: Winkelhalbierende und Sehnenviereck
Fźr den rechnerischen Beweis arbeiten wir mit den Bezeichnungen der Abbildung 2.
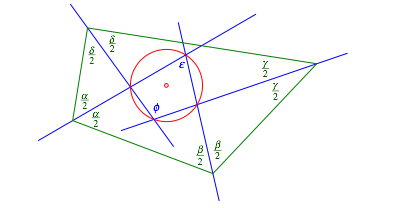
Abb. 2: Bezeichnungen
Es ist:
![]() (1)
(1)
Damit wird wegen der Winkelsumme ą im beliebigen Viereck:
![]() (2)
(2)
Dies war zu zeigen.
Analog laufen alle folgenden Nachweise der Sehnenviereckeigenschaft.
Die Šu§eren Winkelhalbierenden des allgemeinen Vierecks bilden ebenfalls ein Sehnenviereck (Abb. 3). Beweis mit der Winkeleigenschaft.
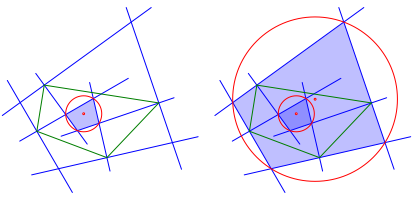
Abb. 3: €u§ere Winkelhalbierende
3 Verdrehung der Winkelhalbierenden
3.1 Gleiche Drehwinkel
Wir drehen die inneren Winkelhalbierenden des beliebigen Vierecks um die Eckpunkte um je denselben, aber beliebigen Winkel. In der Abbildung 4 ist der Drehwinkel 20ˇ im Uhrzeigersinn gewŠhlt worden. Die verdrehten Winkelhalbierenden bilden wiederum ein Sehnenviereck. Beweis mit der Winkeleigenschaft.
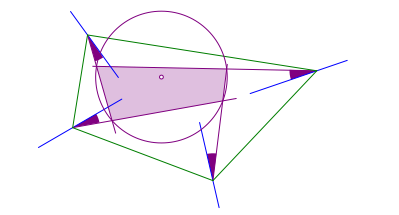
Abb. 4: Verdrehte Winkelhalbierende
3.2 Thaleskreis
Der Mittelpunkt des Umkreises des neuen Sehnenviereckes liegt auf dem Thaleskreis źber den Mittelpunkten der Umkreise der beiden durch die inneren und Šu§eren Winkelhalbierenden generierten Sehnenvierecke (Abb. 5). Dieser Sachverhalt ist allerdings nur mit DGS verifiziert worden. Der Autor hat keinen Beweis und freut sich źber jeden Hinweis dazu.
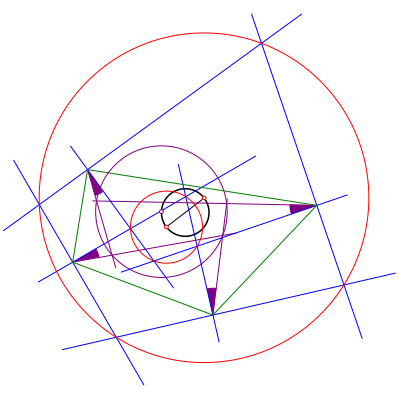
Abb. 5: Thaleskreis
3.3 Individuelles Verdrehen
Wir wŠhlen vier Drehwinkel, deren alternierende Summe verschwindet. In der Abbildung 6 sind die Winkel 40ˇ, 34ˇ, 20ˇ, 26ˇ gewŠhlt worden.
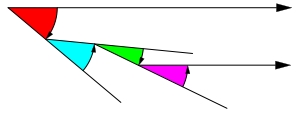
Abb. 6: Alternierende Winkelsumme null
Nun verdrehen wir die Winkelhalbierenden des beliebigen Viereckes der Reihe nach um diese Winkel (Drehsinn beachten) (Abb. 7).
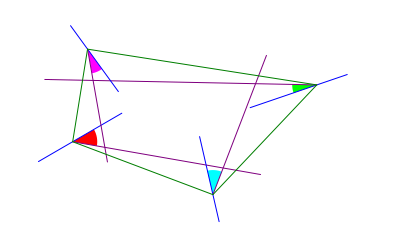
Abb. 7: Individuelle Verdrehungen
Die verdrehten Winkelhalbierenden bilden ein Sehnenviereck (Abb. 8). Beweis mit der Winkeleigenschaft.
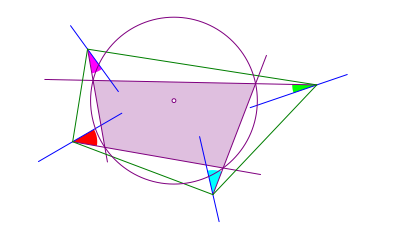
Abb. 8: Sehnenviereck
3.4 Die geklauten Winkel
Die alternierende Summe der Innenwinkel eines Sehnenviereckes ist null. Wir kšnnen daher die Innenwinkel eines beliebigen Sehnenviereckes, allenfalls multipliziert mit einer beliebigen Zahl, fźr das individuelle Verdrehen der Winkelhalbierenden verwenden.
Websites
[1] Hans Walser: Sehnenviereck (11. 4. 2017)
http://www.walser-h-m.ch/hans/Miniaturen/S/Sehnenviereck/Sehnenviereck.htm