Hans Walser, [20120401]
Schwerpunkte nach Archimedes
1
Worum es geht
Wir konstruieren den
Eckenschwerpunkt eines Vieleckes nach den Hebelgesetzen. Die Frage ist, auf wie
viele Arten dies mglich ist.
2
Beispiele
2.1
Eineck
Das Eineck besteht nur
aus einem Punkt, und dieser ist sein eigener Schwerpunkt.
2.2
Zweieck
Bei zwei Punkten ist
der Mittelpunkt ihrer Strecke der Schwerpunkt. Diese Konstruktion kann nur auf
eine Art durchgefhrt werden (Abb. 1).

Abb. 1: Der Mittelpunkt
ist Schwerpunkt
2.3
Dreieck
Wir verbinden zwei der
drei Dreiecksecken. Deren Schwerpunkt ist der Mittelpunkt. In diesem Punkt
hngen zwei Massen. Nun verbinden wir diesen (lokalen) Schwerpunkt mit der
dritten Dreiecksecke, wir zeichnen also die Seitenhalbierende. Da wir an einem
Ende (Seitenmitte) dieser Seitenhalbierenden zwei Massen haben, am anderen Ende
(Dreiecksecke) aber nur eine, mssen wir fr den Schwerpunkt dritteln. Der
Schwerpunkt ist ein Drittel von der Seitenmitte entfernt. Das ist dann auch der
Schwerpunkt aller drei Dreiecksecken.
Diese Konstruktion kann
auf drei Arten durchgefhrt werden (Abb. 2).
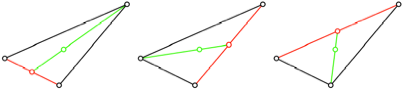
Abb. 2: Drei
Konstruktionen des Schwerpunktes
Die berlagerung der
drei Figuren ist von der Schule her bekannt (Abb. 3).
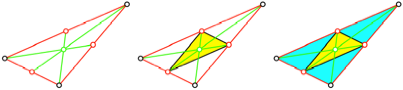
Abb. 3: berlagerung
Das gelb markierte
Dreieck (Seitenmittendreieck) ist lngenm§ig halb so gro§ wie das
Ausgangsdreieck. Es ergibt sich aus dem Ausgangsdreieck durch eine zentrische
Streckung am Schwerpunkt mit dem Faktor ![]() . Der Flcheninhalt des gelben Dreiecks ist ein Viertel des
Flcheninhaltes des Ausgangsdreieckes. Dies kann durch eine Parkettierung
gezeigt werden.
. Der Flcheninhalt des gelben Dreiecks ist ein Viertel des
Flcheninhaltes des Ausgangsdreieckes. Dies kann durch eine Parkettierung
gezeigt werden.
2.4
Viereck
Die Abbildung 4 zeigt
ein Beispiel fr das Viereck. Zuerst wird halbiert (rot), dann gedrittelt
(grn) und dann geviertelt (blau).
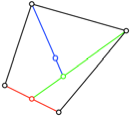
Abb. 4: Viereck
Es geht aber auch
anders (Abb. 5). Da wird ausschlie§lich halbiert.
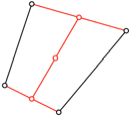
Abb. 5: Halbieren
Auf wie viele Arten
kann im Viereck der Schwerpunkt nach Archimedes gefunden werden?
Fr Konstruktionen vom
Typ der Abbildung 4 whlen wir zunchst einen Eckpunkt (4 Mglichkeiten) und
verbinden mit einem anderen Eckpunkt (3 Mglichkeiten, rot). Dann zeichnen wir
den Mittelpunkt dieser Strecke (rot) und verbinden mit einem weiteren Eckpunkt
(noch 2 Mglichkeiten, grn. Diese Strecke dritteln wir. Der Drittelpunkt
(grn) nher beim Mittelpunkt des ersten Konstruktionsschrittes ist der
Schwerpunkt der bislang verwendeten Eckpunkte. Wir verbinden diesen grnen
Schwerpunkt mit der verbleibenden Ecke (nur eine Mglichkeit, blau) und
vierteln. Der Viertelpunkt (blau) nahe beim Schwerpunkt des zweiten
Konstruktionsschrittes ist der Schwerpunkt der vier Eckpunkte.
Der erste Schritt (rot)
wird bei dieser kombinatorischen Abzhlung allerdings doppelt gezhlt. Fr die
Gesamtzahl der Konstruktionen nach dem Typ der Abbildung 4 ergeben sich somit ![]() Mglichkeiten.
Die Abbildung 6 listet diese explizit auf.
Mglichkeiten.
Die Abbildung 6 listet diese explizit auf.
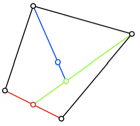
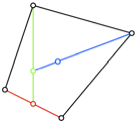
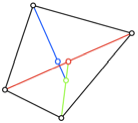
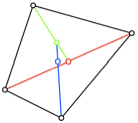
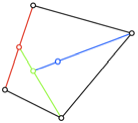
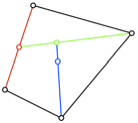

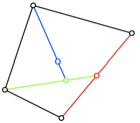
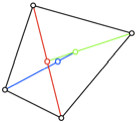
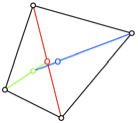
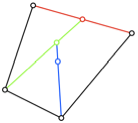
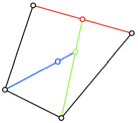
Abb. 6: Die zwlf
Beispiele
Fr die Konstruktionen
vom Typ der Abbildung 5 mssen wir die 4 Eckpunkte in Paare aufteilen. Dazu
gibt es ![]() Mglichkeiten.
Der Mittelpunkt der Mittelpunkte der beiden Paare ist jeweils der Schwerpunkt
der vier Ecken. Bei diesen Konstruktionen mssen wir lediglich halbieren. Die
Abbildung 7 listet die drei Flle explizit auf.
Mglichkeiten.
Der Mittelpunkt der Mittelpunkte der beiden Paare ist jeweils der Schwerpunkt
der vier Ecken. Bei diesen Konstruktionen mssen wir lediglich halbieren. Die
Abbildung 7 listet die drei Flle explizit auf.
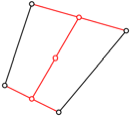
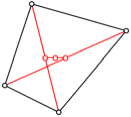
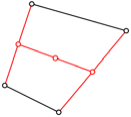
Abb. 7: Drei Flle mit Halbieren
Es gibt also insgesamt
15 Flle. Die Abbildung 8 zeigt die berlagerung dieser 15 Flle.
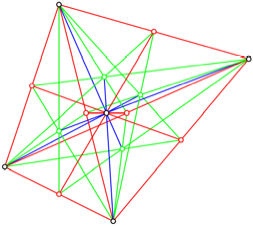
Abb. 8: berlagerung
Die drei in der
Abbildung 9 markierten Viereck sind Parallelogramme. Das erste ist ein
Ladenhter der Schulgeometrie.
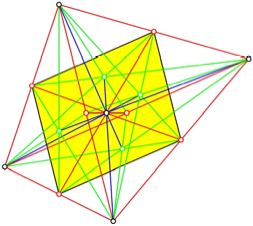
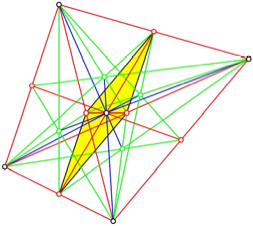
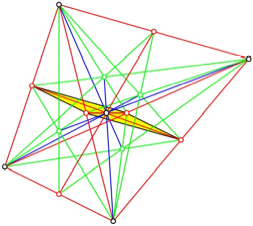
Abb. 9: Drei
Parallelogramme
Das in der Abbildung 10
markierte gelbe Viereck ist hnlich zum Ausgangsviereck. Es ergibt sich aus dem
Ausgangsviereck durch eine zentrische Streckung am Schwerpunkt mit dem Faktor ![]() .
.
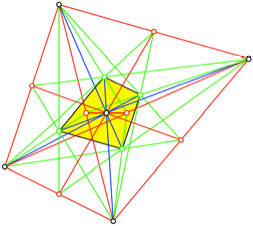
Abb. 10: hnliches
Viereck
Flchenm§ig ist das
gelbe Viereck ein Neuntel des Ausgangsviereck. Ein Versuch, dies durch eine
Parkettierung zu zeigen, scheitert (Abb. 11). An den Ecken des Ausgangsviereckes
erscheinen Parallelogramme, welche nicht gleich gro§ sind.
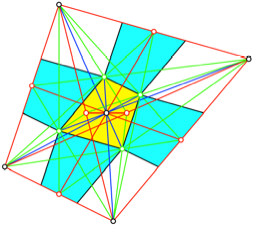
Abb. 11: Keine
Parkettierung
Wenn wir doch
parkettieren (man kann mit jedem Viereck ein Parkett bauen), ergibt sich eine
Umrissfigur mit neun Ecken, welche Flchengleich zum Ausgangsviereck ist (Abb.
12).
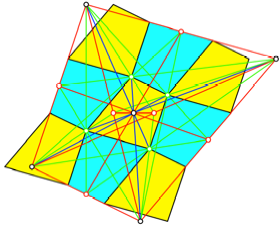
Abb. 12: Parkettierung
Die Flchengleichheit
der beiden Figuren kann auch mit einem Zerlegungsbeweis gezeigt werden (Abb.
13).
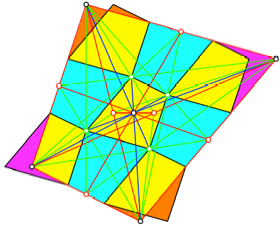
Abb. 13:
Zerlegungsbeweis
2.5
Fnfeck
Die Abbildung 14 zeigt
zwei verschiedene Beispiele fr das Fnfeck. Die gefllten Punkte illustrieren
die bentigten Teilverhltnisse. Der Schwerpunkt ist schwarz gezeichnet.
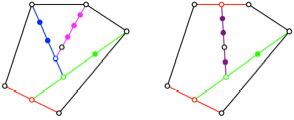
Abb. 14: Fnfeck
Wer Lust hat, kann sich
berlegen, wie viele Flle es beim Fnfeck insgesamt gibt.
3
Abzhlung
Wir bezeichnen mit ![]() die Anzahl der
Flle beim n-Eck.
die Anzahl der
Flle beim n-Eck.
3.1
Bereits bekannte Beispiele
Aus unseren Beispielen
erhalten wir die Tabelle 1.

Tab. 1: Beispiele
3.2
Eine Rekursionsformel
Wir gehen davon aus,
dass wir ![]() fr
fr ![]() kennen und
suchen eine Rekursionsformel fr
kennen und
suchen eine Rekursionsformel fr ![]() .
.
Dazu unterteilen wir
die n in zwei nichtleere disjunkte
Teilmengen von k und ![]() Punkten. Dies
geht auf
Punkten. Dies
geht auf ![]() Arten. Zur
Teilmenge von k Punkten knnen
wir auf
Arten. Zur
Teilmenge von k Punkten knnen
wir auf ![]() Arten den
Schwerpunkt konstruieren, zur Komplementrmenge auf
Arten den
Schwerpunkt konstruieren, zur Komplementrmenge auf ![]() Arten. Nun
unterteilen wir die Verbindungsstrecke der Schwerpunkte der beiden Teilmengen
im Verhltnis
Arten. Nun
unterteilen wir die Verbindungsstrecke der Schwerpunkte der beiden Teilmengen
im Verhltnis ![]() und erhalten so
den Schwerpunkt der n Punkte.
Somit ist:
und erhalten so
den Schwerpunkt der n Punkte.
Somit ist:
![]()
Der Faktor ![]() ist
erforderlich, weil die Teilmengen fr j
Punkte sowohl fr
ist
erforderlich, weil die Teilmengen fr j
Punkte sowohl fr ![]() wie auch fr
wie auch fr ![]() bercksichtigt
werden. Die Summe luft von 1 bis
bercksichtigt
werden. Die Summe luft von 1 bis ![]() , weil die Teilmengen mindestens 1 und hchstens
, weil die Teilmengen mindestens 1 und hchstens ![]() Elemente
enthalten.
Elemente
enthalten.
Mit Hilfe dieser
Rekursionsformel und dem Startwert ![]() erhalten wir die
Werte der Tabelle 2, Spalte 2.
erhalten wir die
Werte der Tabelle 2, Spalte 2.
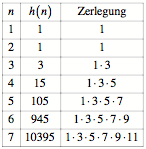
Tab. 2: Beispiele.
Zerlegung
Die Zahlen werden rasch
gro§. Aus der dritten Spalte der Tabelle 2 ergibt sich die Vermutung fr eine explizite
Formel:
![]()
Fr den Beweis dieser
expliziten Formel arbeiten wir mit den Catalan-Zahlen. Die Anregung dazu
erhielt ich von P. W. in A..
3.3
Catalan-Zahlen
Eugne Charles Catalan,
(1814 in Brgge – 1894), belgischer Mathematiker
Definition der
Catalan-Zahlen:
![]()
Numerisch:

Fr die Catalan-Zahlen
gilt die Rekursion von Segner 1758 (Johann Andreas von Segner, 1704 in Pressburg (Bratislava) –
1777 in Halle):
![]()
Mit Hilfe der
Catalan-Zahlen knnen wir die vermutete explizite Formel umschreiben:
![]()
3.4
Beweis der expliziten Formel
Zu zeigen ist: ![]() erfllt die
Rekursion
erfllt die
Rekursion
![]()
mit dem Startwert ![]() .
.
Startwert: ![]() ok.
ok.
Rekursion:
Linke Seite: ![]()
Rechte Seite:
![]()
Nun verwenden wir die
Rekursion von Segner: ![]()
Zunchst ist:
![]()
Durch Umindizieren
ergibt sich:
![]()
Somit erhalten wir fr
die rechte Seite:
![]()
Dies ist gleich der
linken Seite.
Die explizite Formel
ist bewiesen.